Mod Tree
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5934 Accepted Submission(s): 1498
Problem Description
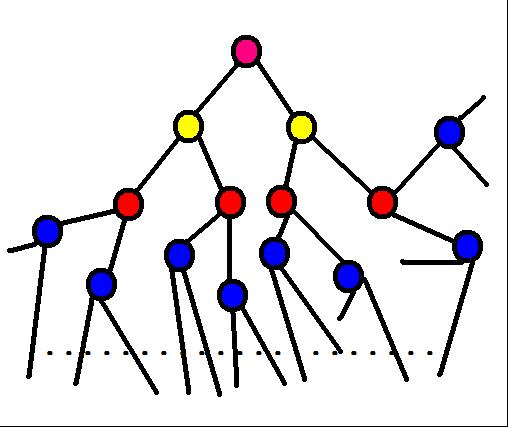
The picture indicates a tree, every node has 2 children.
The depth of the nodes whose color is blue is 3; the depth of the node whose color is pink is 0.
Now out problem is so easy, give you a tree that every nodes have K children, you are expected to calculate the minimize depth D so that the number of nodes whose depth is D equals to N after mod P.
Input
The input consists of several test cases.
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)
Output
The minimize D.
If you can’t find such D, just output “Orz,I can’t find D!”
If you can’t find such D, just output “Orz,I can’t find D!”
Sample Input
3 78992 453
4 1314520 65536
5 1234 67
Sample Output
Orz,I can’t find D!
8
20
扩展baby_step,giant_step算法模板题

1 #include<stdio.h> 2 #include<algorithm> 3 #include<queue> 4 #include<stack> 5 #include<string.h> 6 #include<iostream> 7 #include<math.h> 8 #include<map> 9 using namespace std; 10 typedef long long LL; 11 typedef struct node 12 { 13 LL val; 14 int id; 15 } ss; 16 LL quick(LL n,LL m,LL mod); 17 pair<LL,LL>ex_gcd(LL n,LL m); 18 LL gcd(LL n,LL m); 19 bool cmp(node p,node q); 20 LL g_step_b_step(LL x,LL k,LL z); 21 ss ans[100000]; 22 int main(void) 23 { 24 LL x,z,k; 25 while(scanf("%lld %lld %lld",&x,&z,&k)!=EOF) 26 { 27 LL ask = g_step_b_step(x,k,z); 28 if(ask == -1||k >= z) 29 printf("Orz,I can’t find D! "); 30 else printf("%lld ",ask); 31 } 32 return 0; 33 } 34 LL g_step_b_step(LL x,LL k,LL z) 35 { 36 LL y = 0; 37 LL xx = 1; 38 while(true) 39 { 40 LL c = xx%z; 41 if(c == k)return y; 42 LL gc = gcd(x,z); 43 if(gc == 1)break; 44 y++;if(k%gc)return -1; 45 z/=gc;k /= gc; 46 xx = xx*(x/gc); 47 xx%=z; 48 } 49 LL zz = sqrt(z) + 1; 50 pair<LL,LL>NI = ex_gcd(x,z); 51 NI.first = (NI.first%z + z)%z; 52 LL NNI = NI.first*(k%z)%z; 53 ans[0].id = 0,ans[0].val = k; 54 for(int i = 1; i <= zz; i++) 55 { 56 ans[i].id = i; 57 ans[i].val = NNI; 58 NNI = NNI*NI.first%z; 59 } 60 sort(ans,ans+zz+1,cmp); 61 LL x1 = quick(x,zz,z); 62 LL slx = xx; 63 for(int i = 0; i <= zz; i++) 64 { 65 int l = 0,r = zz; 66 int id = -1; 67 while(l <= r) 68 { 69 int mid = (l+r)/2; 70 if(ans[mid].val >= slx) 71 { 72 id = mid; 73 r = mid - 1; 74 } 75 else l = mid + 1; 76 } 77 if(id!=-1) 78 { 79 if(ans[id].val == slx) 80 { 81 LL ask = (LL)i*zz + ans[id].id + y; 82 return ask; 83 } 84 } 85 slx = slx*x1%z; 86 } 87 return -1; 88 } 89 LL gcd(LL n,LL m) 90 { 91 if(m == 0) 92 return n; 93 else return gcd(m,n%m); 94 } 95 LL quick(LL n,LL m,LL mod) 96 { 97 n%=mod; 98 LL ask = 1; 99 while(m) 100 { 101 if(m&1) 102 ask = ask*n%mod; 103 n = n*n%mod; 104 m/=2; 105 } 106 return ask; 107 } 108 pair<LL,LL>ex_gcd(LL n,LL m) 109 { 110 if(m == 0) 111 return make_pair(1,0); 112 else 113 { 114 pair<LL,LL>ans = ex_gcd(m,n%m); 115 return make_pair(ans.second,ans.first - (n/m)*ans.second); 116 } 117 } 118 bool cmp(node p,node q) 119 { 120 if(p.val == q.val) 121 return p.id < q.id; 122 else return p.val < q.val; 123 }
