介绍
本文记录了 Efficient Knowledge Graph Accuracy Evaluation 的实现过程。目前实现了在随机生成的三元组上进行 static evaluation 和 incremental evaluation。
Github 地址:https://github.com/zzk0/KGAccEval
整体结构
整体结构采用论文中描述的结构。
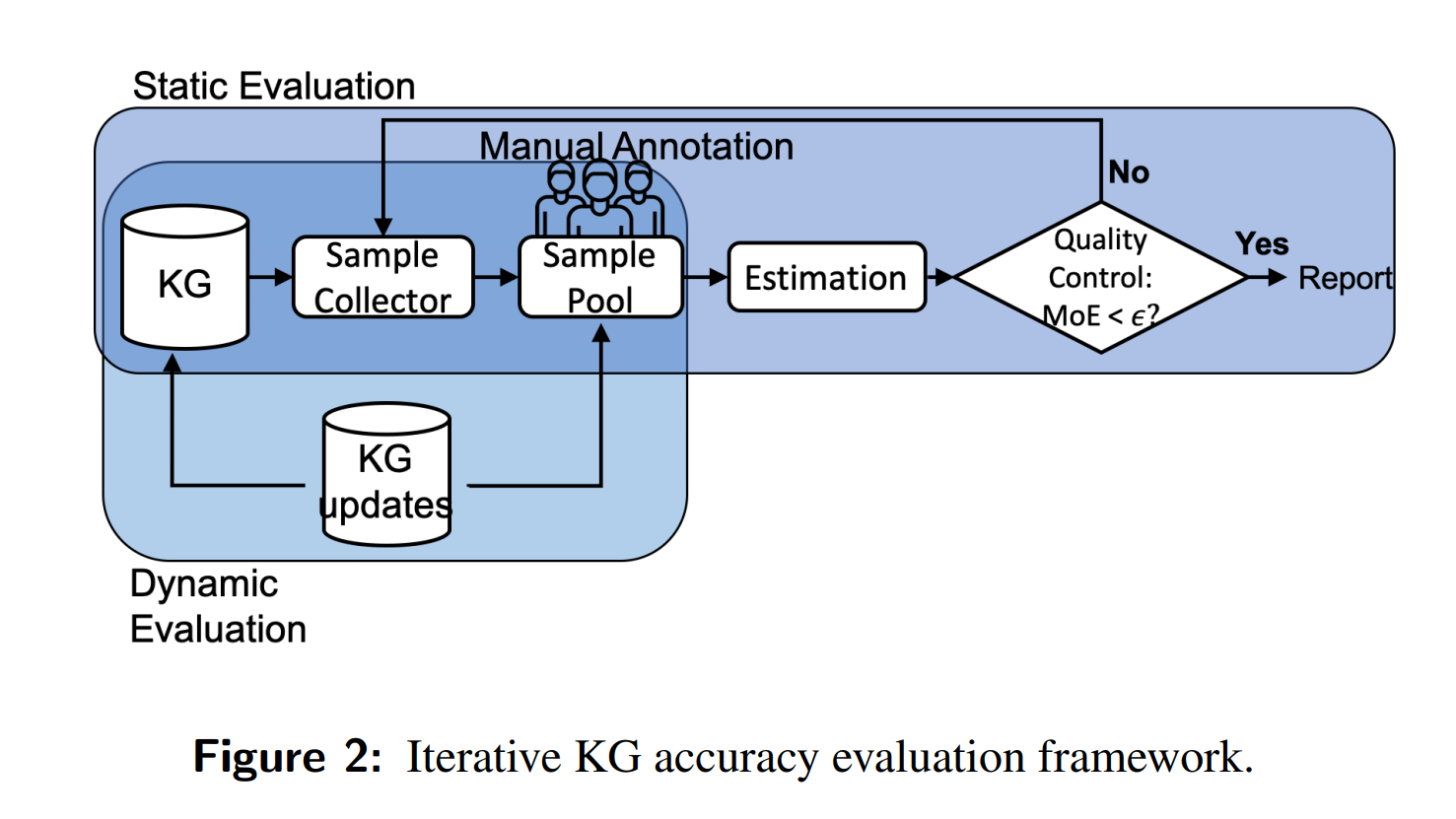
文件结构:
KnowledgeGraph, SamplePool, SampleCollector, Estimation 这几个类相对比较独立,由 Evaluation 这个类来组织和调用。

Static Evaluation
具体可参考 Evalution.java 这个文件。
1, 抽样条件
根据以下条件决定是否需要继续抽样,一个是检查误差界限是否大于目标值,一个是检查是否还能继续抽取。
this.estimation.getMarginOfError() > this.epsilon && remainTriples
2,抽样过程
根据方法去抽样,调用对应的 SampleCollector,将得到的样本放入 SamplePool,同时计算每一次抽样的估计量。计算估计量,比如 SRS 中估计量就是每一个样本正确与否,正确为 1,错误为 0。再比如 TWCS 中估计量就是一个实体的样本正确率。
3,调用例子
double suggestedAccuracy = 0.73;
KnowledgeGraph kg = new KnowledgeGraph();
kg.init(suggestedAccuracy, 1000);
Evaluation evaluation = new Evaluation(epsilon, alpha, Method.TWCS);
acc = evaluation.evaluate(kg);
System.out.println(acc);
Incremental Evaluation
增量评估在实现的时候,总想着不去改动代码来做,但是面对变化,保持不变是不行的。
增量评估分为 ReservoirIncrementalEvaluation 和 StratifiedIncrementalEvaluation,两个是独立的类,虽然可以抽象出共同的 evalute 接口。这个部分实现的时候,根据论文中描述的两个算法的需要,去获取 Evalutaion 中的信息,所以需要在 Evalutaion 中增加一些获取信息的方法。
这个部分没有实现完全,对于蓄水池算法的增量评估,如果 MoE 小于目标值了呢?我没有做处理。
调用例子:
// base evaluation
Evaluation evaluation = new Evaluation(epsilon, alpha, Method.TWCS);
acc = evaluation.evaluate(kg);
System.out.println(acc);
ReservoirIncrementalEvaluation incrementalEvaluation = new ReservoirIncrementalEvaluation();
incrementalEvaluation.init(evaluation, kg);
StratifiedIncrementalEvaluation incrementalEvaluation1 = new StratifiedIncrementalEvaluation();
incrementalEvaluation1.init(evaluation, kg);
double[] accs = {0.27, 0.8, 0.2, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.9};
for (int i = 0; i < accs.length; i++) {
// update evaluation
KnowledgeGraph update = new KnowledgeGraph();
update.init(accs[i], 1000);
System.out.println("---------------------------------------");
double newAccuracy = incrementalEvaluation.evaluate(update);
System.out.println("Reservoir Incremental Evaluation: " + newAccuracy);
newAccuracy = incrementalEvaluation1.evaluate(update);
System.out.println("Stratified Incremental Evaluation: " + newAccuracy);
}
实现细节
如何随机生成知识图谱数据
我们随机产生知识图谱的三元组,三元组的内容是空的,但是预先给它确定是正确还是错误。
KnowledgeGraph 类中有一个方法 init,需要传入准确率和实体个数。对每一个实体,随机确定实体的三元组个数,并且随机改变这个实体的准确率,之后进行伯努利实验,产生一个 0 到 1 之间的随机数,检查是否小于准确率(也在 0 和 1 之间),如果是,那么产生的三元组为正确的三元组,如果否,那么产生的三元组为错误的三元组。
随机采样
简单随机采样,假设三元组一共有 n 个。有两种简单随机采样的方法。
第一种,产生一个 [0, n) 的整数随机数,用散列表来记录这个随机数是否产生过,如果没有,那么抽取这个随机数对应的三元组;如果有,那么重新执行这个过程。不过这种方法有问题,当我们抽取的三元组越来越多,重新抽取的次数会越来越多,如果只有 100 个三元组,并且我们抽取了 99 个,那么要抽取到最后一个三元组的期望次数是 100.
第二种,产生一个 List,这个 List 顺序放入 [0, n),然后使用 Collections.shuffle 打乱。从头开始抽取即可。
加权采样
加权采样的方法有二种。
第一种,类似随机采样的第一种。因为抽取的是实体,所以直接产生一个 [0, n) 的整数随机数,这个随机数落到的那个实体就被抽取出来。如果实体的三元组个数越多,那么被抽取的概率越大。同样,使用一个散列表记录是否抽取过,这个方法同样存在缺陷。
第二种,蓄水池算法。给每个实体一个 key,(r = Rand(0,1), key = r^{1 / size}),选取前 k 大个 key。
正态分布分位点
浙大版概率论中第 50 页有分位点的定义。
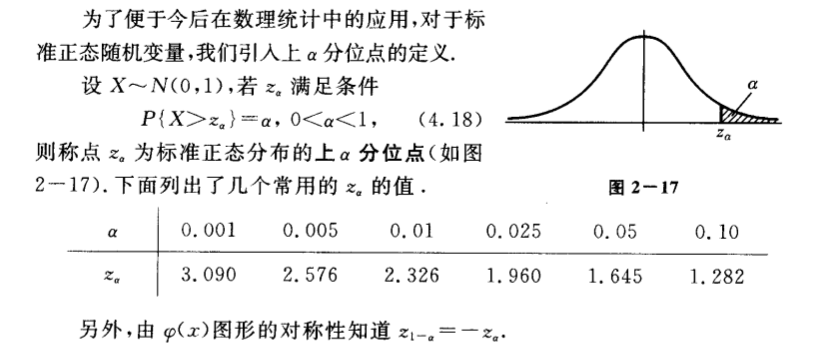
我们要找 (alpha) 的置信区间,需要找到 (z_frac{1-alpha}{2}) 这个点,使到正态分布落在大于(z_frac{1-alpha}{2}) 的概率为 (frac{1-alpha}{2}),这样可以构造一个对称区域,落到两边的概率为 (1-alpha),落到中间的概率就是 (alpha) 了。
那么这个分位点如何计算呢?查了一下,有一个叫做 Hastings formula 的东西[1],可以计算上 (alpha) 分位点。
比如对于 95% 的置信区间,我们需要调用 computeZx(0.025) 去计算分位点。
private double computeZx(double alpha) {
double[] c = {2.515517, 0.802853, 0.010328};
double[] d = {0.0, 1.432788, 0.189269, 0.001308};
double y = Math.sqrt(-2 * Math.log(alpha));
double cy = 0, dy = 0;
for (int i = 0; i < 2; i++) {
cy = cy + c[i] * Math.pow(y, i);
dy = dy + d[i + 1] * Math.pow(y, i+1);
}
return y - cy / (dy + 1);
}
static evaluation 正确性
假设我们需要求解 90% 的置信区间,5% 的误差界限,这意味着准确率误差范围在 5% 以内的概率为 90%。
在 Example.java 这个文件中,我们重复进行了 100 次实验,计算准确落在误差范围内的比例,大致接近 90%。
BTW,误差界限含义,顾名思义就是误差的范围。
Reservoir Incremental Evaluation
假设我们要采样总体 (G + Delta) 的样本,可是我们只有采样了 (G) 的样本,如何采样 (Delta) 才能得到 (G + Delta) 的样本呢?
这就是蓄水池算法的优越之处了:蓄水池算法可以在不了解总体的情况下,进行采样!
假设 (G) 是 TWCS 采样的结果,我们是根据实体三元组多少加权随机抽样的。我们可以将其视为对 (G) 使用蓄水池算法计算的结果,所以当新的三元组加进来的时候,我们按照蓄水池算法运行下去,就可以得到 (G + Delta) 的结果。
我在实验的时候,一开始我的做法是保持原来的加权抽样的代码不变。我们可以拿到加权采样的结果,比如有 60 个实体。于是,我对这 60 个实体计算蓄水池算法的 key。可是这些 key 的大小其实分布得比较散,在进行增量更新的时候,计算的 key 大部分会覆盖原来的那些,把原来的样本替换掉。
道理很简单,我加权挑出来的这 60 个 key,是先挑再算权值,不是先算权值再挑的。假如增量更新有 1000 个实体,那么相当于随机产生 1060 个key,再去挑选最大的几个。这里有点强者生存的感觉,对于原来的那 60 个 key,如果是先计算 key 再挑选,那么留下来的 key 都是比较“强”的。如果是先挑,再计算 key,那么这些 key 比较随机,容易被后面的强者替代。所以这个部分,我将原来加权抽样的代码做了更改,先计算 key,再挑选。在增量评估的初始化的时候,获取这些 key。
增量评估
开始做这个部分时,一直在想如何尽可能不要改懂代码来实现。
这种想法是徒然的,妄图在不改变代码的情况下增加新功能。代码还是要改,要加点代码。不过现在回想起来,其实,原来的代码结构还行吧,至少做到了一点:对扩展开放,对修改封闭。修改代码是尽量减少了,除了那个加权采样的算法必须得改之外,其他地方保持不动。
有待解决的问题
- 在蓄水池算法的增量评估当中,这个部分实现的不完整。当蓄水池算法抽样完成之后,还需要重新计算 MoE,检查是否在范围内,如果不在,那么还需要再抽样。
- 在蓄水池算法的增量评估当中,当进行多次增量的时候,比如原知识图谱正确率为 0.5,不断地添加正确率为 0.9 的知识图谱,此时会发现正确率上升的很慢。因为蓄水池当中的那些个随机数都是身经百战,强者生存下来的,所以很难被替代。
- 论文提供了增量评估的方法,却没有提供“减量”评估的方法。我认为可以这样处理,假设使用的是 TWCS 评估的结果,并且 TWCS 使用的加权采样是由蓄水池算法来实现的,那么我们可以去掉“减量”,重新挑选前 k 大的实体。
- 论文中说,按照实体的三元组多少的分层是不理想的。那么该如何分层呢?论文中直接使用实体的正确率来分层,得出的实验结果很美好,暗示了合理的分层有助于提高评估的效率。
- 使用正态分布还是使用 t 分布?虽然在样本多的情况下,差异是不大的,但是仍然有可能出现样本小的情况。
参考文献
[1] https://wenku.baidu.com/view/3ca32836581b6bd97f19ea8c.html?re=view