回文字符串,想必大家不会不熟悉吧?
回文串会求的吧?暴力一遍O(n^2)很简单,但当字符长度很长时便会TLE,简单,hash+二分搞定,其复杂度约为O(nlogn), 而Manacher算法能够在线性的时间内处理出最长回文子串。
让我们来看道题:http://acm.hdu.edu.cn/showproblem.php?pid=3068

这个算法的巧妙之处,便是把奇数的回文串和偶数的回文串统一起来考虑了。这一点一直是在做回文串问题中时比较烦的地方。这个算法还有一个很好的地方就是充分利用了字符匹配的特殊性,避免了大量不必要的重复匹配。那怎么去实现呢?
我们要求字符串s中最长的回文子串
Manacher重新构造了一个新数组,在每两个字符中间插入一个'#',如下图:
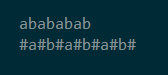
我们很容易发现,如果出现这种情况(如下图)在处理第三个字符('#')市,会发现扫到左侧时候可能会出现越界

为了避免索引数超出数组边界值做字符比较,可以在处理过的字符串的第一个位置(索引为0的位置)加入一个区分字符,笔者喜欢用'@'。
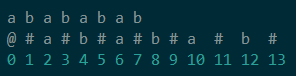
上图便是处理过的样子。(编号表示数组位数,3表示是s[3]的字符)
我们现在用p[i]数组表示以字符s[i]为中心的回文半径(如p[3] = 1)。
我们很容易发现最长子序列的长度刚好是(p[i] - 1)。
那么我们怎么来求p[i]数组呢?
步骤如下:
当处理到[i]的时候,我们去找0-i中是否存在一个数(设为id)使得p[id] + id > i,设mx = p[id] + id。
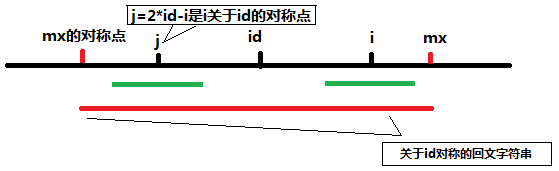
如上图,由于红的字符串是回文字符串,所以关于j对称的回文子串和关于i对称的回文子串是完全一样的(图中两段绿色的线条),而满足mx-i>P[j]时说明此时j的回文子串半径小于j到mx关于j对称的左端点的差,此时可以初始化P[i]=P[j]。但如果绿色部分超出id的回文串呢?
如下图:
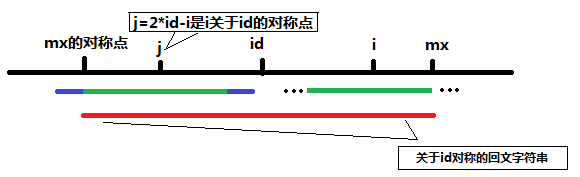
紫色表示以j为中心的回文串超出以id为中心的回文半径的部分(即图中红色部分)由于红的字符串是回文字符串,所以关于j对称的回文子串和关于i对称的在mx和mx的对称点之间的回文子串是完全一样的(图中两段绿色的线条),而满足mx-i<=P[j]时说明此时j的回文子串半径大于或等于j到mx关于j对称的左端点的差,此时可以初始化P[i]=mx-i,超出部分只能一个个判断。再对P[i]的回文子串半径进行进一步的增大。(以上两图均取自参考论文)
综上所述初始化p[i] = min(p[j], mx - i);
对于超出回文字符串部分(即红色部分,我们只能一个一个的去判断)
即while(s[i + p[i]] == s[i - p[i]])p[i] += 1;
当mx <= i 的时候我们只能将p[i] 初始化为1(对于它都是未知的,只能通过一位一位去比较)。
附上总代码:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 const int N = 220000 + 5; 6 7 char s[N]; 8 9 int p[N]; 10 11 int n, id, mx; 12 13 void work(){ 14 id = mx = 0; 15 int ans = 0; 16 n = strlen(s); 17 for(int i = n; i >= 0; i --){ 18 s[2 * i + 2] = s[i]; 19 s[2 * i + 1] = '#'; 20 } 21 s[0] = '@'; 22 p[0] = 1; 23 for(int i = 1; i < 2 * n + 2; i ++){ 24 if(mx > i)p[i] = min(p[2 * id - i], mx - i); 25 else p[i] = 1; 26 while(s[i + p[i]] == s[i - p[i]]) p[i] += 1; 27 if(mx < p[i] + i){ 28 id = i; 29 mx = p[i] + i; 30 } 31 ans = max(ans, p[i] - 1); 32 } 33 printf("%d\n", ans); 34 } 35 36 int main(){ 37 while(scanf("%s", s) == 1)work(); 38 return 0; 39 }
