如果只是对一个整数进行素性测试的只要o(√n)的复杂度便可以判定,蓝而如果是n个呢(n<=1000)照样可以,那如果100000个呢?对于普通的o(n√n)根本跑不动,因此我们必须寻找更加高效的算法,常用的筛选方法有埃氏筛法, 区间筛法,欧拉筛法。
1.埃氏筛法
首先,我们先把2-n范围内的数写下来,其中最小的素数是2,那么能被2整除的数便不是素数,那么我们可以把2的倍数都划去。然后剩下的最小素数便是3,我们便把3的倍数都划去,以此类推。这样反复操作我们就能枚举n以内的素数。

贴上伪代码:
1 const int N = 1000000 + 5; 2 int check[N], prime[N]; 3 4 int ptot = 0; 5 memset(check, 0, sizeof(check)); 6 for(int i = 2; i <= n; i ++){ 7 if(!check[i])prime[ptot++] = i; 8 for(int j = 2; i * j <= n; j ++) check[i * j] = 1; 9 }
但是问题又来了, 这个复杂度究竟该怎么算呢?怎么看像o(n2)呢?No No No~~
每次我们筛去每个数的整数倍像2筛了n/2个,3筛了n/3个;
因此总的复杂度约为:
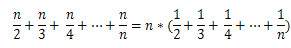
哎呀!这不是发散级数吗?这个不是发散的数啊,那复杂度不是会爆掉吗?
别担心,虽然它是发散级数,但是他的增长速度非常慢,来我们测试一下
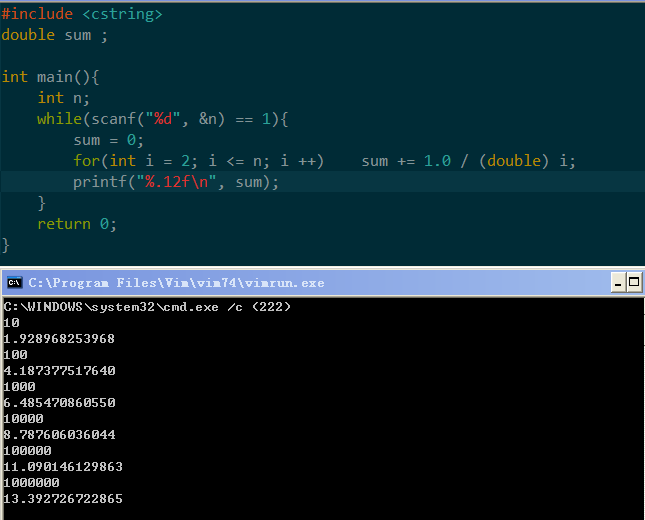
看到了吗?这个发散级数在n = 1000000的时候都没有超过14由此可见它的复杂度很小,近似等效成o(nloglogn),而对我们这些搞ACM的人来讲他大致看成线性的都无妨。
2.区间筛法
设区间[a,b)表示a<=x<b,的素数所构成的集合。
我们很容易知道b只要不能整除[2,√b]里面的素数,那么b就可以被认定为一个素数,因此,如果我们有√b里面的素数表,便可以结合埃氏筛法来判断。
附上伪代码:
1 const int N = 100000 + 5; 2 int check[N], prime[N]; 3 int is_prime[N]; 4 5 int ptot = 0; 6 memset(check, 0, sizeof(check)); 7 memset(is_prime, 0, sizeof(is_prime)); 8 for(int i = 2; i <= n; i ++){ 9 if(!check[i])prime[ptot++] = i; 10 for(int j = 2; i * j <= sqrt(b); j ++) check[i * j] = 1;//筛[2,√b) 11 for(int j = a/i+1; i * j < b; j ++) is_prime[i * j - a] = 0;//筛[a,b) 12 //将[a, b)的数,移到[0, b - a)可节省空间 13 }
3.欧拉筛法
这便是重头戏,真真正正的o(n)的复杂度,不说什么,直接上代码。
1 const int N = 1000000 + 5; 2 int prime[N], check[N]; 3 4 memset(prime, 0, sizeof(prime)); 5 memset(check, 0, sizeof(check)); 6 int ptot = 0; 7 for(int i = 2; i <= n; i ++){ 8 if(!check[i]) prime[ptot ++] = i; 9 for(int j = 0; j < ptot; j ++){ 10 if(prime[j] * i > n) break; 11 check[prime[j] * i] = 1; 12 if(i % prime[j] == 0) break; 13 } 14 }
这个貌似只是做了少许改进了吧,貌似就改进了第12行啊,聪明,蓝而就是因为这一行,导致了他的复杂度变成完美的线性, 设合数的最小质因数为p,则当它遍历到这个素数的时候因为第12行二跳出循环,这样直接导致了每个合数只能被它的最小质因数给删去。
下面给出证明:
设合数n的最小质因数为p,另一个比它大的质因数为p1,设 n = p1 * m1 = p * m,我们很容易就可以发现j循环到质因数p的时候合数n第一次被标记(若循环到p之前已经跳出循环则说明有比p更小的质因数),若也被p1标记,则是在这之前(因为p1 > p,所以m1 < m),考虑i循环到m1,注意到n = p*m=p1*m1且p,p1为不同的质数,因此p|m1,所以当j循环到质数p后就结束,不会循环到p1.这就说明了不会被p1筛去,说明合数只能被它最小的素数给删去。(很神奇吧!)