http://acm.hdu.edu.cn/showproblem.php?pid=4757
题意:
给出一棵树,每个结点有一个权值,现在有多个询问,每次询问包含x,y,z三个数,求出在x到y的路径上与z最大的异或值。
思路:
看着别人的代码做完这道题目之后觉得这题和主席树求第k小是异曲同工的,主席树求第k小是对每个数建立一棵线段树,也就是说第i棵线段树记录的是区间[1,i]之间的数,这样的话[l,r]这个区间内的数就在第l棵线段树和第r棵线段树之间。
回到这题上来,这题也是要在一个范围之内寻找一个值,但是它不是数组,而是树结构,所以类似的也可以对每个结点建立字典树,记录根结点到该结点的所有权值。图解如下:
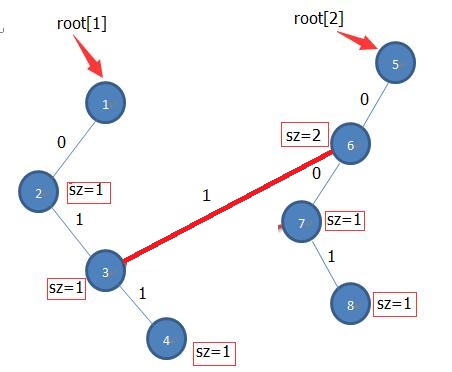
假设现在只有两个结点1和2,1是2的父亲结点,1的权值为3,2的权值为1。对1建立字典树如图左所示,对2建立字典树时如图右所示,5->6->7->8就是结点2的字典树,5->6->3->4就是结点1的字典树。所以我们对某个结点建立字典树时,就包含了根结点到该结点路径上所有点权值的情况。图中的sz表示的就是前缀出现的数量,为什么root[2]的前缀0的sz是2呢,因为一个来自1结点的,另一个是自己的,所有在计算sz值的时候,先继承父亲结点的sz,然后再加上自身的。
有了这个sz值之后,我们就可以进行查询操作了,先计算出x和y的最近公共祖先z,那么如果判断前缀是否存在就是t[t[x].son[!c]].sz+t[t[y].son[!c]].sz-2*t[t[z].son[!c]].sz>0。这样的话没有计算z,所以最后还要单独计算一下和z节点的异或值。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<vector> 5 using namespace std; 6 const int maxn = 1e5 + 5; 7 8 int n, m, num, Log; 9 int root[maxn], a[maxn], dep[maxn], p[maxn][20]; 10 11 vector<int> G[maxn]; 12 13 struct Trie 14 { 15 int son[2]; 16 int sz; 17 }t[100*maxn]; 18 19 void init(int x) 20 { 21 t[x].sz = 0; 22 memset(t[x].son,0,sizeof(t[x].son)); 23 } 24 25 void insert(int x, int y, int val) 26 { 27 x = root[x], y = root[y]; 28 for(int i=15;i>=0;i--) 29 { 30 int c = (val>>i)&1; 31 if(!t[x].son[c]) 32 { 33 num++; init(num); 34 t[x].son[c] = num; 35 t[x].son[c^1] = t[y].son[c^1]; 36 t[t[x].son[c]].sz = t[t[y].son[c]].sz; 37 } 38 x = t[x].son[c], y = t[y].son[c]; 39 t[x].sz++; 40 } 41 } 42 43 void dfs(int u, int fa) 44 { 45 num++; init(num); 46 root[u] = num; 47 p[u][0] = fa; 48 dep[u] = dep[fa]+1; 49 insert(u,fa,a[u]); 50 for(int i=0;i<G[u].size();i++) 51 { 52 int v = G[u][i]; 53 if(v==fa) continue; 54 dfs(v,u); 55 } 56 } 57 58 void LCA_init() 59 { 60 for(int j=1;j<=Log;j++) 61 for(int i=1;i<=n;i++) 62 p[i][j] = p[p[i][j-1]][j-1]; 63 } 64 65 int LCA(int x, int y) 66 { 67 if(x==y) return x; 68 if(dep[x]<dep[y]) swap(x,y); 69 for(int i=Log;i>=0;i--) 70 { 71 if(dep[p[x][i]] >= dep[y]) x=p[x][i]; 72 } 73 if(x==y) return x; 74 for(int i=Log;i>=0;i--) 75 { 76 if(p[x][i]!=p[y][i]) {x=p[x][i];y=p[y][i];} 77 } 78 return p[x][0]; 79 } 80 81 82 int query(int x, int y, int val) 83 { 84 int z = LCA(x,y); 85 int tmp = a[z]^val; 86 x = root[x], y = root[y], z = root[z]; 87 int ans = 0; 88 for(int i=15;i>=0;i--) 89 { 90 int c = (val>>i)&1; 91 if(t[t[x].son[!c]].sz+t[t[y].son[!c]].sz-2*t[t[z].son[!c]].sz>0) 92 { 93 ans+=(1<<i); 94 c^=1; 95 } 96 x = t[x].son[c]; 97 y = t[y].son[c]; 98 z = t[z].son[c]; 99 } 100 return max(ans,tmp); 101 } 102 103 int main() 104 { 105 //freopen("in.txt","r",stdin); 106 while(~scanf("%d%d",&n,&m)) 107 { 108 memset(p,0,sizeof(p)); 109 memset(root,0,sizeof(root)); 110 num = 0; init(0); 111 for(int i=1;i<=n;i++) {scanf("%d",&a[i]); G[i].clear();} 112 for(int i=1;i<=n-1;i++) 113 { 114 int u,v; 115 scanf("%d%d",&u,&v); 116 G[u].push_back(v); 117 G[v].push_back(u); 118 } 119 dep[0] = 0; 120 dfs(1,0); 121 122 n++; 123 for(Log=0;(1<<Log)<=n;Log++); 124 Log--; 125 LCA_init(); 126 127 while(m--) 128 { 129 int x,y,z; 130 scanf("%d%d%d",&x,&y,&z); 131 printf("%d ",query(x,y,z)); 132 } 133 134 } 135 return 0; 136 }