POJ 1704 Georgia and Bob（阶梯博弈）

 http://poj.org/problem?id=1704

题意：

在一维的棋盘上有n颗棋子，有两个人玩游戏，每次可以将任意一颗棋子向左移动任意格（但是移到最左边就不能再移了，并且如果前面有棋子挡着，那也无法移动），最后不能移动者输。

思路：
借这道题学习了一波阶梯博弈。

阶梯博弈的话就是两两配对组成尼姆博弈（如果棋子数为奇数的话，第一颗棋子就和左边第一个格子配对）。见下图：

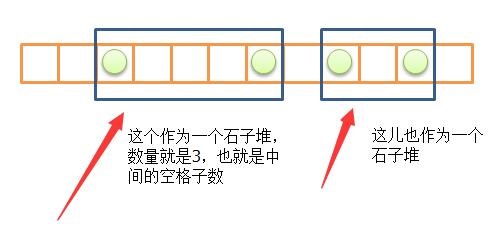
每对移动右边的棋子就相当于是在取石子，最后谁要是先移动成了下面的情形，那它肯定就输了。

这个时候就是两两之间不存在格子，也就是没石子了，正好对应于尼姆博弈。

可能有人会觉得玩家会移动每对左边的棋子来增加石子破坏状态，但其实这是不可能的。首先，如果是先手必胜状态，那么赢家没必要这样做，其次，如果是先手必败时，输家这么做，那么赢家完全可以移动右棋子恢复状态。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

int n;
int a[1005];

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i=1;i<=n;i++)  scanf("%d",&a[i]);
        sort(a+1,a+n+1);
        int ans = 0;
        a[0] = 0;
        for(int i=n;i>0;i-=2)
        {
            ans^= (a[i] - a[i-1] -1);
        }
        if(ans) puts("Georgia will win");
        else puts("Bob will win");
    }
    return 0;
}