参考书《数据压缩导论(第4版)》 Page 100
5、给定如表4-9所示的概率模型,求出序列a1a1a3a2a3a1 的实值标签。

解 :
p(a1)=0.2;p(a2)=0.3;p(a3)=0.5
x(a1)=i;F(0)=0;F(1)=0.2;F(2)=0.5;F(3)=1
u(n)=1, l(n)=0
u(n)=l(n-1)+(u-l)*F(xn)
l(n)=l(n-1)+(u-l)*F(xn-1)
a1, u1=l0+(u0-l0)*Fx(1)=0.2;
l1=l0+(u0-l0)*Fx(0)=0;
a1, u2=l1+(u1-l1)*Fx(1)=0.04;
l2=l1+(u1-l1)*Fx(0)=0;
a3, u3=l2+(u2-l2)*Fx(3)=0.04;
l3=l2+(u2-l2)*Fx(2)=0.02;
a2, u4=l3+(u3-l3)*Fx(2)=0.03;
l4=l3+(u3-l3)*Fx(1)=0.024;
a3, u5=l4+(u4-l4)*Fx(3)=0.03;
l5=l4+(u4-l4)*Fx(2)=0.027;
a1, u6=l5+(u5-l5)*Fx(1)=0.0276;
l6=l5+(u5-l5)*Fx(0)=0.027;
所以该序列a1a1a3a2a3a1的实值标签Tag(a1a1a3a2a3a1)=1/2(u6+l6)=0.0273.
6、对于表4-9所示的概率模型,对于一个标签为0.63215699的长度为10的序列进行解码。
include
int main()
{
double tag=0.63215699;
double l[100],u[100];
double t;
l[0]=0;
u[0]=1;
double A0=0.0,A1=0.2,A2=0.5,A3=1.0;
int M[100];
for(int k=1;k<=10;k++)
{
t=(double)(tag-l[k-1])/(u[k-1]-l[k-1]);
if(t>=A0&&t<=A1)
{
u[k]=l[k-1]+(u[k-1]-l[k-1])A1;
l[k]=l[k-1]+(u[k-1]-l[k-1])A0;
M[k]=1;
}
else if(t>A1&&t<=A2)
{
u[k]=l[k-1]+(u[k-1]-l[k-1])A2;
l[k]=l[k-1]+(u[k-1]-l[k-1])A1;
M[k]=2;
}
else if(t>A2&&t<=A3)
{
u[k]=l[k-1]+(u[k-1]-l[k-1])A3;
l[k]=l[k-1]+(u[k-1]-l[k-1])A2;
M[k]=3;
}
printf("%d",M[k]);
}
return 0;
}
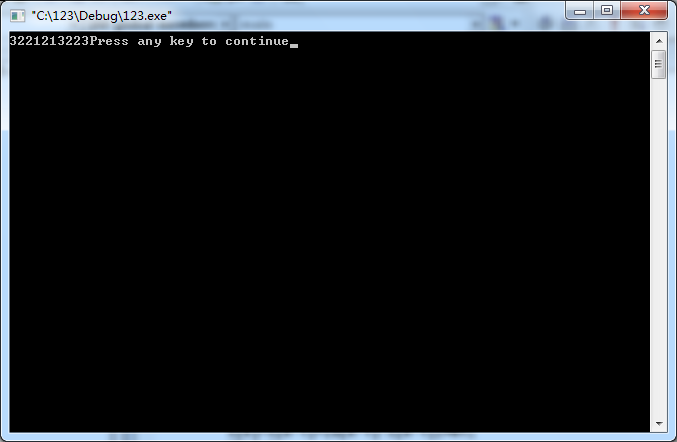
编码的结果为:3221213223.