题面
题解
恩, 我们首先有这两个关系
[displaystyleegin{aligned} F_j &= sum_{i < j}frac{q_iq_j}{(i - j)^2} - sum_{i > j}frac{q_iq_j}{(i - j)^2}\ &= q_jcdot(sum_{i < j}frac{q_i}{(i - j)^2}-sum_{i>j}frac{q_i}{(i - j)^2})end{aligned}
]
然后由
[displaystyle E_i = frac{F_i}{q_i}
]
我们可以推出这样的式子
[displaystyleegin{aligned}
E_i&=frac{F_i}{q_i}\&=sum_{j<i}frac{q_j}{(i - j)^2}-sum_{j>i}frac{q_j}{(j - i)^2}\
end{aligned}
]
我们来看一下 n = 3 的情况
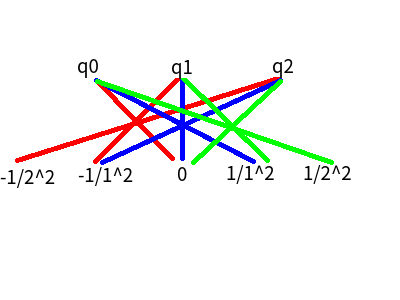
我们将红色的线的两端乘起来, 再把三条红线的和相加就得到了(E_0), 同理我们通过蓝线, 绿线可以得到(E_1), (E_2)
我们定义(a_i = p_i), (b_i = frac{1}{i ^ 2}), 特别的, 我们定义(b_{-i} = -frac{1}{i ^ 2}), 先别管为什么下标为负
[displaystyleegin{aligned}
E_0&=a_0b_0+a_1b_{-1}+a_2b_{-2}\
E_1&=a_0b_1+a_1b_0+a_2b_{-1}\
E_2&=a_0b_2+a_1b_1+a_2b_0
end{aligned}
]
恩, 我们来讨论数组下标小于零的问题, 整体平移就行了嘛, 注意到(b)最小的下标为((-3 + 1)), 所以我们平移((3 - 1))位就可以了, 所以有:
[egin{aligned}
E_0&=a_0b_2+a_1b_1+a_2b_0Leftrightarrow E_0 = sum_{i+j=2}a_ib_j\
E_1&=a_0b_3+a_1b_2+a_2b_1Leftrightarrow E_1 = sum_{i+j=3}a_ib_j\
E_2&=a_0b_4+a_1b_3+a_2b_2Leftrightarrow E_2 = sum_{i+j=4}a_ib_j
end{aligned}
]
恩, 我们来看一下卷积的形式
[c_k = sum_{i + j = k}a_ib_j
]
我们会发现这里的(E)数组的下标离可以卷积差了一个((3 - 1)), 用(E_2)代替(E_0)就可以用(a)与(b)的卷积来算了
我们将特殊情况扩展到一般情况, 设(E)共有(n)项, 自己瞎猜一下可以发现(b)数组下标平移了(n - 1)位, (E)数组的下标平移了(n - 1)位, 所以, 最后我们输出(E)的第([n - 1, (n - 1) + n - 1])项即可
这篇题解就是写给我们这种蒟蒻看的, 至于卷积, 我猜各位是为了练习FFT才来做这道题的吧
Code
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <vector>
#include <cmath>
#define itn int
#define reaD read
#define N 1000005
const double pi = acos(-1);
using namespace std;
int n, m, cnt, rev[N];
struct complex
{
double x, y;
complex(double xx = 0, double yy = 0) { x = xx; y = yy; }
complex operator + (complex p) { return complex(x + p.x, y + p.y); }
complex operator - (complex p) { return complex(x - p.x, y - p.y); }
complex operator * (complex p) { return complex(x * p.x - y * p.y, x * p.y + y * p.x); }
} a[N], b[N];
inline int read()
{
int x = 0, w = 1; char c = getchar();
while(c < '0' || c > '9') { if (c == '-') w = -1; c = getchar(); }
while(c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
return x * w;
}
void FFT(complex* p, int opt)
{
for(int i = 0; i < m; i++) if(i < rev[i]) swap(p[i], p[rev[i]]);
for(int i = 1; i < m; i <<= 1)
{
complex cur = complex(cos(pi / i), opt * sin(pi / i));
for(int j = 0; j < m; j += (i << 1))
{
complex w = complex(1, 0);
for(int k = 0; k < i; k++, w = w * cur)
{
complex l = p[j + k], r = w * p[i + j + k];
p[j + k] = l + r; p[i + j + k] = l - r;
}
}
}
}
int main()
{
n = read();
for(int i = 0; i < n; i++) scanf("%lf", &a[i].x);
for(int i = 1; i < n; i++)
{
b[i + n - 1].x = 1 / (1.0 * (double) i * i);
b[n - 1 - i].x = -b[i + n - 1].x;
}
for(m = 1; m <= 3 * n - 2; m <<= 1, cnt++);
for(int i = 0; i < m; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
FFT(a, 1); FFT(b, 1);
for(int i = 0; i <= m; i++) a[i] = a[i] * b[i];
FFT(a, -1);
for(int i = n - 1; i <= 2 * n - 2; i++) printf("%.3lf
", a[i].x / m);
return 0;
}
这可能是我写得最认真的一篇题解吧, 希望看这篇题解的泥萌可以康懂