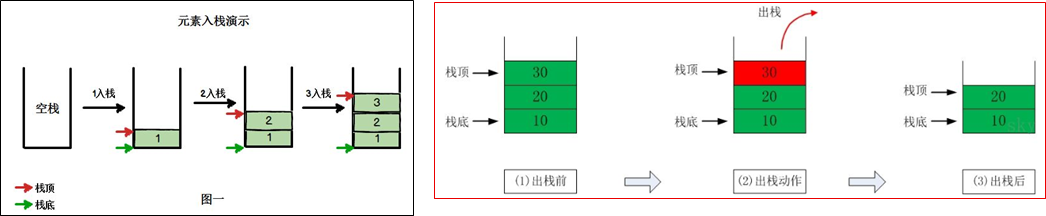
1、栈的介绍

![]()
2、栈的应用场景
1)子程序的调用:在跳往子程序前,会先将下一个指令的地址存储到堆栈中,知道子程序执行完成后再将地址取出,以回到原来的程序中。
2)处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
3)表达式的转换【中缀表达式转成后缀表达式】与求职。
4)二叉树的遍历。
5)图形的深度优先(depth-first)搜索法。
3、栈的快速入门
1)用数组模拟栈的使用,由于栈是一种有序列表,当然可以用数组的数据结构来存储栈的数据内容。
2)示意图:

3)代码实现:
package com.stack; import java.util.Scanner; public class ArrayStackDemo { public static void main(String[] args) { ArrayStack arrayStack = new ArrayStack(10); String key = ""; Scanner sc = new Scanner(System.in); boolean loop = true; while (loop) { System.out.println("push:添加数据入栈"); System.out.println("pop:添加数据出栈"); System.out.println("list:遍历栈数据"); System.out.println("exit:退出"); key = sc.next(); switch (key) { case "push": System.out.println("请输入一个数据"); int value = sc.nextInt(); arrayStack.push(value); break; case "pop": int reval = arrayStack.pop(); System.out.println("出栈的数据为:" + reval); break; case "list": arrayStack.list(); break; case "exit": sc.close(); loop = false; break; default: break; } } System.out.println("程序退出~~~~~~~~"); } } //定义一个ArrayStack栈 class ArrayStack { private int maxSize; private int[] stack; private int top = -1; public ArrayStack(int maxSize) { this.maxSize = maxSize; stack = new int[maxSize]; } //栈满 public boolean isFull() { return top == maxSize - 1; } //栈空 public boolean isEmpty() { return top == -1; } //入栈 public void push(int data) { if (isFull()) { System.out.println("栈满了,不能加入数据"); return; } top++; stack[top] = data; } //出栈 public int pop() { if (isEmpty()) { System.out.println("栈空的,不能取数据"); return 0; } int redata = stack[top]; top--; return redata; } //遍历栈 public void list() { if (isEmpty()) { System.out.println("栈空的,不能取数据"); return; } for (int i = 0; i < stack.length; i++) { System.out.printf("stack[%d]=%d ", i, stack[i]); } } }
4、使用栈做一个逆波兰计算器(后缀表达式)

代码实现:
package com.stack; import java.util.ArrayList; import java.util.List; import java.util.Stack; public class PolandNotation { public static void main(String[] args) { String exp = "4 5 * 8 - 60 + 8 2 / +"; List<String> list = getListString(exp); int res = calculate(list); System.out.println("计算结果为:"+res); } //后缀表达式的计算 public static int calculate(List<String> ls){ Stack<String> stack = new Stack<>(); for(String item:ls){ if(item.matches("\d+")){//匹配的是多位数 stack.push(item); }else{ //pop出两个数,并计算,计算完成后再入栈 int num1 = Integer.parseInt(stack.pop()); int num2 = Integer.parseInt(stack.pop()); int result = 0; if(item.equals("+")){ result = num2+num1; }else if(item.equals("-")){ result = num2-num1; }else if(item.equals("*")){ result = num2*num1; }else if(item.equals("/")){ result = num2/num1; }else{ System.out.println("运算符有误"); } stack.push(""+result); } } return Integer.parseInt(stack.pop()); } //将一个后缀表达式,放入到ArrayList中 public static List<String> getListString(String expression){ String[] split = expression.split(" "); List<String> list = new ArrayList<>(); for(String s:split){ list.add(s); } return list; } }
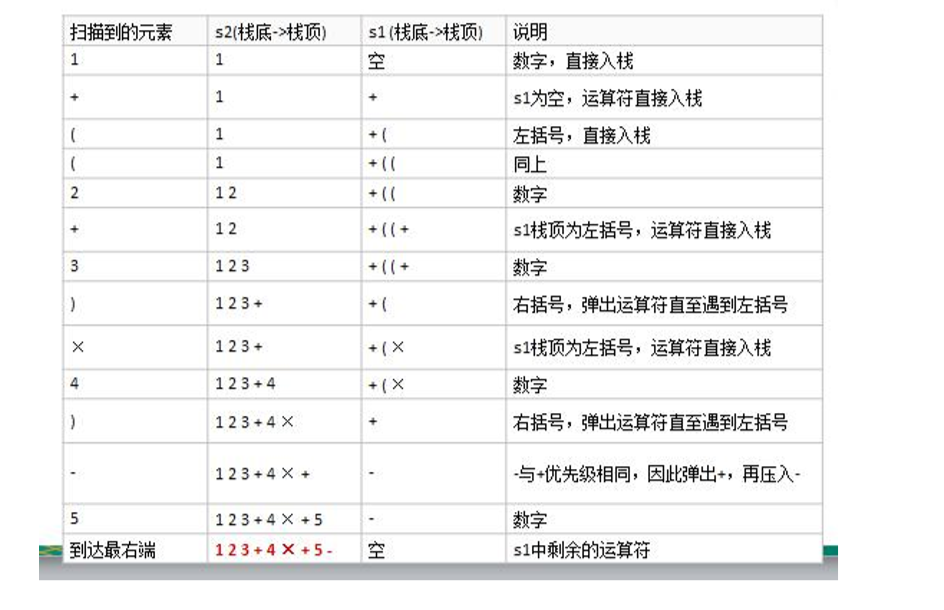
5、中缀表达式转换后缀表达式
具体思路步骤如下:

举例:

代码实现:
//将得到的中缀表达式对应的list转成对应的后缀表达式 public static List<String> parseSuffixExpression(List<String> ls){ Stack<String> s1= new Stack<>();//符号栈 List<String> l1 = new ArrayList<>();//结果栈,存放中间结果 for(String item:ls){ if(item.matches("\d+")){ l1.add(item); }else if(item.equals("(")){ s1.add(item); }else if(item.equals(")")){ //如果是右括号,则依次弹出是s1栈顶的运算符,并压入l1,直到遇到左括号,并消除左括号 while (!s1.peek().equals("(")){ l1.add(s1.pop()); } s1.pop();//弹出左小括号 }else {//比较运算符的优先级 //当item的优先级小于等于s1栈顶运算符,将s1栈顶的运算符弹出并加入到l1 //再比较 while (s1.size()>0 && getValue(s1.peek()) >= getValue(item)){ l1.add(s1.pop()); } //如果是大于当前s1栈顶的优先级,则直接压入 s1.push(item); } } while(s1.size()!=0){ l1.add(s1.pop()); } return l1; } //比较运算符的优先级 public static int getValue(String operation){ int result = 0; switch (operation){ case "+": result = 1; break; case "-": result = 1; break; case "*": result = 2; break; case "/": result = 2; break; default: System.out.println("不存在该运算符"); break; } return result; }