看了下SPFA题解,一个一个太麻烦了,另一个写的很不清楚,而且注释都变成了"????"不知道怎么过的,于是自己来一发SPFA算法。
Part 1.题意
M 个仓库,卖给 N 个商店,两个问,第一问求运价最小值,第二问最大值。
显然是一个最小费用最大流(MCMF)。
Part 2.思路
1.连让每个仓库连接一个超级源点 SS ,费用(dis)为0,流量为仓库的流量,表示每个仓库最多可以运出多少货物。
2.让每一个仓库连接每一家商店,边权为 cost[i][j] ,其中,i为仓库编号,j为商店编号编号,流量为 need[j] ,其实流量可以取得范围是 [need[j]...INF] ,另外如果出现 need[j] <这个仓库货物量的情况也可以不怕(这时候取值的下限变成 min(hw[i],need[j]) ) hw指的是这家仓库的货物,还有注意编号的范围(我默认超级源点是 00 ,仓库是 1……n ,商店是 n+1……n+m ,超级汇点是 10000)
3.让每一家商店连接超级汇点 TT
图像帮助理解: 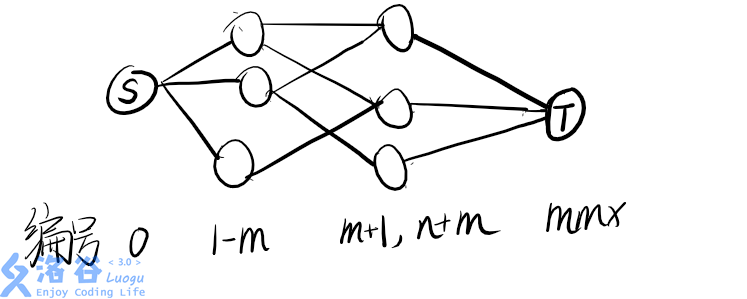
Part 3.代码
现在代码就好办了 注释给的很清楚
1 #include<iostream> 2 #include<cmath> 3 #include<cstdio> 4 #include<cstring> 5 #include<queue> 6 #include<stack> 7 #include<vector> 8 #include<map> 9 #include<set> 10 #include<algorithm> 11 12 #define I_copy_this_answer return 0; 13 14 using namespace std; 15 16 int n,m,head[1100],size=1; 17 int mmx=1000,mincost,maxwater; 18 int flow[1100]; 19 int need[1100],cost[310][310]; 20 int pre[1100],las[1100],dis[1100],vis[1100],hw[1100]; 21 22 struct edge{ 23 int next,to,dis,flow; 24 }e[100860]; 25 26 void addedge(int next,int to,int dis,int flow) 27 { 28 e[++size].to=to; 29 e[size].dis=dis; 30 e[size].flow=flow; 31 e[size].next=head[next]; 32 head[next]=size; 33 } 34 35 int spfa(int s) 36 { 37 memset(flow,0x3f,sizeof(flow)); 38 memset(dis,0x3f,sizeof(dis)); 39 memset(vis,0,sizeof(vis)); 40 queue <int> q; 41 q.push(s); 42 dis[s]=0; 43 vis[s]=1; 44 pre[mmx]=-1; //(其实只要不是与p直接连的点(n+1......n+m)就可以了 45 while(!q.empty()) 46 { 47 int t=q.front(); 48 q.pop(); 49 vis[t]=0; 50 int i,j,k,l; 51 for(i=head[t];i;i=e[i].next) 52 { 53 j=e[i].to; 54 k=e[i].dis; 55 l=e[i].flow; 56 if(dis[t]+k<dis[j]&&l>0) //没有流量的话这条路就增广不了,最短距离是建立在增广路存在的基础上的 57 { 58 dis[j]=dis[t]+k; 59 las[j]=i; //las指的是这个点(j)与上个点(t)相连的边的编号 60 pre[j]=t; //pre指的是这条路径上这个点(j)的上一个点 61 flow[j]=min(flow[t],l); //把当前边流量与上个点的流量对比,解决出现仓库货物比需要的少的情况 62 if(!vis[j]) 63 { 64 q.push(j); 65 vis[j]=1; 66 } 67 } 68 } 69 } 70 return pre[mmx]!=-1; //如果不是这个值就说明这个点被刷新,增广成功 71 } 72 73 void mcmf() 74 { 75 while(spfa(0)) 76 { 77 mincost+=dis[mmx]*flow[mmx]; //从源点出发到汇点的单位费用再乘以单位,由于每次只增广一条路,而且仓库和商店是直接连接的,可以这样写 78 int t=mmx; 79 while(t!=0) 80 { 81 e[las[t]].flow-=flow[mmx]; //回溯,修改每条边的流量,因为该算法中途找到的增广路不是最后的增广路,所以这个要等到最后来改变 82 e[las[t]^1].flow+=flow[mmx]; 83 t=pre[t]; 84 } 85 } 86 } 87 88 void build_edge(int t) 89 { 90 int i,j; 91 for(i=1;i<=m;i++) 92 { 93 addedge(0,i,0,hw[i]); 94 addedge(i,0,0,0); 95 } 96 for(i=1;i<=m;i++) 97 for(j=1;j<=n;j++) 98 { 99 addedge(i,j+m,cost[i][j]*t,need[j]); 100 addedge(j+m,i,-cost[i][j]*t,0); 101 } 102 for(i=1;i<=n;i++) 103 { 104 addedge(i+m,mmx,0,need[i]); 105 addedge(mmx,i+m,0,0); 106 } 107 } 108 109 int main() 110 { 111 int i,j; 112 scanf("%d %d",&m,&n); 113 for(i=1;i<=m;i++) 114 { 115 int t1; 116 scanf("%d",&hw[i]); 117 } 118 for(i=1;i<=n;i++) 119 scanf("%d",&need[i]); 120 for(i=1;i<=m;i++) 121 for(j=1;j<=n;j++) 122 scanf("%d",&cost[i][j]); //读入,与上面的cost,need,hw如果不明白可以对照输入格式看代表什么意思 123 build_edge(1); //建立边权为正的边,跑最小费用最大流 124 mcmf();//最小费用最大流(Min Cost Max Flow )的缩写 125 printf("%d",mincost); 126 maxwater=0; 127 mincost=0; 128 size=1; 129 memset(head,0,sizeof(head)); 130 build_edge(-1); 131 mcmf(); 132 printf(" %d",-mincost); 133 I_copy_this_answer 134 }