A - Distinct Sub-palindromes HDU - 6754
题意:询问一个只由小写字母组成的长度为n的字符串最少有多少个回文子串。
思路:找规律,当n<=3时sum=26n,当n>3时我们发现只要前三个字符串固定那么要最少回文子串,后面的位置也固定了比如abcabc.所以sum=26*25*24。

1 #include<bits/stdc++.h> 2 int main() 3 { 4 int t,n; 5 scanf("%d",&t); 6 while(t--) 7 { 8 scanf("%d",&n); 9 if(n==1) puts("26"); 10 else if(n==2) puts("676"); 11 else if(n==3) puts("17576"); 12 else puts("15600"); 13 } 14 }
一开始读错了题,没看到回文串,后面大家都A了才发现是个思维题。
B - Fibonacci Sum HDU - 6755
题意:求这样一个式子。
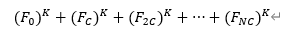
官方题解:

分析:


1 //#include<bits/stdc++.h> 2 #include<time.h> 3 #include <set> 4 #include <map> 5 #include <stack> 6 #include <cmath> 7 #include <queue> 8 #include <cstdio> 9 #include <string> 10 #include <vector> 11 #include <cstring> 12 #include <utility> 13 #include <cstring> 14 #include <iostream> 15 #include <algorithm> 16 #include <list> 17 using namespace std; 18 #define eps 1e-10 19 #define PI acos(-1.0) 20 #define lowbit(x) ((x)&(-x)) 21 #define zero(x) (((x)>0?(x):-(x))<eps) 22 #define mem(s,n) memset(s,n,sizeof s); 23 #define ios {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);} 24 typedef long long ll; 25 typedef unsigned long long ull; 26 const int maxn=1e5; 27 const int Inf=0x7f7f7f7f; 28 const ll Mod=1e9+9; 29 const int N=3e3+5; 30 bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }//判断一个数是不是 2 的正整数次幂 31 int modPowerOfTwo(int x, int mod) { return x & (mod - 1); }//对 2 的非负整数次幂取模 32 int getBit(int a, int b) { return (a >> b) & 1; }// 获取 a 的第 b 位,最低位编号为 0 33 int Max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }// 如果 a>=b,(a-b)>>31 为 0,否则为 -1 34 int Min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); } 35 ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;} 36 ll lcm(ll a, ll b) {return a / gcd(a, b) * b;} 37 int Abs(int n) { 38 return (n ^ (n >> 31)) - (n >> 31); 39 /* n>>31 取得 n 的符号,若 n 为正数,n>>31 等于 0,若 n 为负数,n>>31 等于 -1 40 若 n 为正数 n^0=n, 数不变,若 n 为负数有 n^(-1) 41 需要计算 n 和 -1 的补码,然后进行异或运算, 42 结果 n 变号并且为 n 的绝对值减 1,再减去 -1 就是绝对值 */ 43 } 44 ll binpow(ll a, ll b) { 45 ll res = 1; 46 while (b > 0) { 47 if (b & 1) res = res * a%Mod; 48 a = a * a%Mod; 49 b >>= 1; 50 } 51 return res%Mod; 52 } 53 void extend_gcd(ll a,ll b,ll &x,ll &y) 54 { 55 if(b==0) { 56 x=1,y=0; 57 return; 58 } 59 extend_gcd(b,a%b,x,y); 60 ll tmp=x; 61 x=y; 62 y=tmp-(a/b)*y; 63 } 64 ll mod_inverse(ll a,ll m) 65 { 66 ll x,y; 67 extend_gcd(a,m,x,y); 68 return (m+x%m)%m; 69 } 70 ll eulor(ll x) 71 { 72 ll cnt=x; 73 ll ma=sqrt(x); 74 for(int i=2;i<=ma;i++) 75 { 76 if(x%i==0) cnt=cnt/i*(i-1); 77 while(x%i==0) x/=i; 78 } 79 if(x>1) cnt=cnt/x*(x-1); 80 return cnt; 81 } 82 ll n,c; 83 int k,a[maxn+5],b[maxn+5]; 84 int cmp(int n,int k) 85 { 86 if(n<k) return 0; 87 return (ll)a[n]*b[k]%Mod*b[n-k]%Mod; 88 } 89 int main() 90 { 91 ios 92 a[0]=1; 93 for(int i=1;i<=maxn;i++) a[i]=(ll)a[i-1]*i%Mod; 94 b[maxn]=binpow(a[maxn],Mod-2); 95 for(int i=maxn-1;i>=0;i--) b[i]=(ll)(i+1)*b[i+1]%Mod; 96 int t; 97 cin>>t; 98 while(t--) 99 { 100 cin>>n>>c>>k; 101 int A=691504013,B=308495997; 102 A=binpow(A,c%(Mod-1)); 103 B=binpow(B,c%(Mod-1)); 104 int a=1,b=binpow(B,k); 105 int ib=binpow(B,Mod-2); 106 int ans=0; 107 for(int j=0;j<=k;j++) 108 { 109 int x=(ll)a*b%Mod; 110 if(x==1) x=(n+1)%Mod; 111 else x=(ll)(binpow(x,(n+1)%(Mod-1))-1+Mod)%Mod*binpow((x-1+Mod)%Mod,Mod-2)%Mod; 112 if((k-j)&1)x=x==0?x:Mod-x; 113 ans=((ll)ans+(ll)cmp(k,j)*x)%Mod; 114 a=(ll)a*A%Mod; 115 b=(ll)b*ib%Mod; 116 } 117 int mul=276601605; 118 mul=binpow(mul,k); 119 ans=(ll)ans*mul%Mod; 120 cout<<ans<<endl; 121 } 122 return 0; 123 }
这题完全没想到用到了斐波那契的通项公式,当时一看到1018就毫无下手,晚上补题看了半天题解才看懂(是我太菜了)。
C - Leading Robots HDU - 6759
题意:给你有N个机器人,并且告诉你他们的初始位置和加速度,问最多有几个机器人在某一时刻跑在最前面(最右边的机器人只允许存在一个)。
思路:1.转化为二维凸包问题,x=0.5*at2,建立t2-x的直角坐标系,然后减去重复的直线,跑一边凸包输出凸包的顶点即可(赛后看了博客恍然大悟)。

1 //#include<bits/stdc++.h> 2 #include<time.h> 3 #include <set> 4 #include <map> 5 #include <stack> 6 #include <cmath> 7 #include <queue> 8 #include <cstdio> 9 #include <string> 10 #include <vector> 11 #include <cstring> 12 #include <utility> 13 #include <cstring> 14 #include <iostream> 15 #include <algorithm> 16 #include <list> 17 using namespace std; 18 #define eps 1e-10 19 #define PI acos(-1.0) 20 #define lowbit(x) ((x)&(-x)) 21 #define zero(x) (((x)>0?(x):-(x))<eps) 22 #define mem(s,n) memset(s,n,sizeof s); 23 #define ios {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);} 24 typedef long long ll; 25 typedef unsigned long long ull; 26 const int maxn=1e5+5; 27 const int Inf=0x7f7f7f7f; 28 const ll Mod=1e9+7; 29 const int N=3e3+5; 30 bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }//判断一个数是不是 2 的正整数次幂 31 int modPowerOfTwo(int x, int mod) { return x & (mod - 1); }//对 2 的非负整数次幂取模 32 int getBit(int a, int b) { return (a >> b) & 1; }// 获取 a 的第 b 位,最低位编号为 0 33 int Max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }// 如果 a>=b,(a-b)>>31 为 0,否则为 -1 34 int Min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); } 35 ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;} 36 ll lcm(ll a, ll b) {return a / gcd(a, b) * b;} 37 int Abs(int n) { 38 return (n ^ (n >> 31)) - (n >> 31); 39 /* n>>31 取得 n 的符号,若 n 为正数,n>>31 等于 0,若 n 为负数,n>>31 等于 -1 40 若 n 为正数 n^0=n, 数不变,若 n 为负数有 n^(-1) 41 需要计算 n 和 -1 的补码,然后进行异或运算, 42 结果 n 变号并且为 n 的绝对值减 1,再减去 -1 就是绝对值 */ 43 } 44 ll binpow(ll a, ll b,ll c) { 45 ll res = 1; 46 while (b > 0) { 47 if (b & 1) res = res * a%c; 48 a = a * a%c; 49 b >>= 1; 50 } 51 return res%c; 52 } 53 void extend_gcd(ll a,ll b,ll &x,ll &y) 54 { 55 if(b==0) { 56 x=1,y=0; 57 return; 58 } 59 extend_gcd(b,a%b,x,y); 60 ll tmp=x; 61 x=y; 62 y=tmp-(a/b)*y; 63 } 64 ll mod_inverse(ll a,ll m) 65 { 66 ll x,y; 67 extend_gcd(a,m,x,y); 68 return (m+x%m)%m; 69 } 70 ll eulor(ll x) 71 { 72 ll cnt=x; 73 ll ma=sqrt(x); 74 for(int i=2;i<=ma;i++) 75 { 76 if(x%i==0) cnt=cnt/i*(i-1); 77 while(x%i==0) x/=i; 78 } 79 if(x>1) cnt=cnt/x*(x-1); 80 return cnt; 81 } 82 ll qr(){ 83 ll ret=0,c=getchar(),f=0; 84 while(!isdigit(c)) f|=c==45,c=getchar(); 85 while( isdigit(c)) ret=ret*10+c-48,c=getchar(); 86 return f?-ret:ret; 87 } 88 89 typedef pair<ll,ll> P; 90 P data[maxn],sav[maxn]; 91 bool ans[maxn],repeat[maxn]; 92 int stk[maxn]; 93 94 double operator * (P a,P b){ 95 double ret=1.0*(b.second-a.second)/(a.first-b.first); 96 return ret; 97 } 98 99 void surface(int len){ 100 int top=0; 101 for(int t=1,r=1;r<=len;t=++r){ 102 while(r<len&&data[t].first==data[r+1].first) ++r; 103 t=r; 104 while(top&&data[stk[top]].second<=data[t].second) --top; 105 while(top>1&&data[stk[top]]*data[stk[top-1]]*data[t].first+data[t].second>=data[stk[top]]*data[stk[top-1]]*data[stk[top]].first+data[stk[top]].second) --top; 106 stk[++top]=t; 107 } 108 for(int t=1;t<=top;++t) ans[stk[t]]=1; 109 } 110 111 int main(){ 112 int T=qr(); 113 while(T--){ 114 memset(ans,0,sizeof ans); 115 memset(repeat,0,sizeof repeat); 116 int n=qr(),len=0; 117 for(int t=1;t<=n;++t) 118 sav[t].second=qr()*2,sav[t].first=qr(); 119 sort(sav+1,sav+n+1); 120 len=0; 121 for(int t=1,r=1;r<=n;t=++r){ 122 while(r<n&&sav[r+1]==sav[t]) ++r; 123 data[++len]=sav[t]; 124 if(r!=t) repeat[len]=1; 125 } 126 surface(len); 127 int ret=0; 128 for(int t=1;t<=len;++t) 129 if(ans[t]&&!repeat[t]) ++ret; 130 printf("%d ",ret); 131 } 132 return 0; 133 }
思路:2.首先我们要明白一个点能超过它前面的点,那么他的加速度一定大于其,所以就要对点进行排序,先按照位置排,再按照加速排,一般思维就是枚举每个点但是复杂度是O(n2),显然会Tle,但是我
还是提交了一发。下午吃好饭仔细想了想前面枚举进行了很多没必要的计算。然后想到用stcak 的先进后出特征,每次从栈顶取两个 u1,u2,如果当前位置i能够在u1到达u2之前到达u2,那么pop(u1),因为u1不可能成为leader,如果不能那么就Push(i),i成为新的栈顶,一次次循环。

1 //#include<bits/stdc++.h> 2 #include<time.h> 3 #include <set> 4 #include <map> 5 #include <stack> 6 #include <cmath> 7 #include <queue> 8 #include <cstdio> 9 #include <string> 10 #include <vector> 11 #include <cstring> 12 #include <utility> 13 #include <cstring> 14 #include <iostream> 15 #include <algorithm> 16 #include <list> 17 using namespace std; 18 #define eps 1e-10 19 #define PI acos(-1.0) 20 #define lowbit(x) ((x)&(-x)) 21 #define zero(x) (((x)>0?(x):-(x))<eps) 22 #define mem(s,n) memset(s,n,sizeof s); 23 #define ios {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);} 24 typedef long long ll; 25 typedef unsigned long long ull; 26 const int maxn=1e5+5; 27 const int Inf=0x7f7f7f7f; 28 const ll Mod=1e9+7; 29 const int N=3e3+5; 30 bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }//判断一个数是不是 2 的正整数次幂 31 int modPowerOfTwo(int x, int mod) { return x & (mod - 1); }//对 2 的非负整数次幂取模 32 int getBit(int a, int b) { return (a >> b) & 1; }// 获取 a 的第 b 位,最低位编号为 0 33 int Max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }// 如果 a>=b,(a-b)>>31 为 0,否则为 -1 34 int Min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); } 35 ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;} 36 ll lcm(ll a, ll b) {return a / gcd(a, b) * b;} 37 int Abs(int n) { 38 return (n ^ (n >> 31)) - (n >> 31); 39 /* n>>31 取得 n 的符号,若 n 为正数,n>>31 等于 0,若 n 为负数,n>>31 等于 -1 40 若 n 为正数 n^0=n, 数不变,若 n 为负数有 n^(-1) 41 需要计算 n 和 -1 的补码,然后进行异或运算, 42 结果 n 变号并且为 n 的绝对值减 1,再减去 -1 就是绝对值 */ 43 } 44 ll binpow(ll a, ll b,ll c) { 45 ll res = 1; 46 while (b > 0) { 47 if (b & 1) res = res * a%c; 48 a = a * a%c; 49 b >>= 1; 50 } 51 return res%c; 52 } 53 void extend_gcd(ll a,ll b,ll &x,ll &y) 54 { 55 if(b==0) { 56 x=1,y=0; 57 return; 58 } 59 extend_gcd(b,a%b,x,y); 60 ll tmp=x; 61 x=y; 62 y=tmp-(a/b)*y; 63 } 64 ll mod_inverse(ll a,ll m) 65 { 66 ll x,y; 67 extend_gcd(a,m,x,y); 68 return (m+x%m)%m; 69 } 70 ll eulor(ll x) 71 { 72 ll cnt=x; 73 ll ma=sqrt(x); 74 for(int i=2;i<=ma;i++) 75 { 76 if(x%i==0) cnt=cnt/i*(i-1); 77 while(x%i==0) x/=i; 78 } 79 if(x>1) cnt=cnt/x*(x-1); 80 return cnt; 81 } 82 struct node 83 { 84 ll c,a; 85 int vis; 86 }e[maxn],g[maxn]; 87 int cmp(node a,node b) 88 { 89 if(a.c==b.c) return a.a>b.a; 90 else return a.c>b.c; 91 } 92 int main() 93 { 94 int t,n; 95 scanf("%d",&t); 96 while(t--) 97 { 98 scanf("%d",&n); 99 for(int i=1;i<=n;i++) scanf("%lld%lld",&e[i].c,&e[i].a); 100 sort(e+1,e+n+1,cmp); 101 int cnt=0; 102 for(int i=1;i<=n;i++) 103 { 104 if(g[cnt].c==e[i].c&&g[cnt].a==e[i].a) g[cnt].vis=1; 105 if(g[cnt].a<e[i].a) 106 { 107 cnt++; 108 g[cnt].c=e[i].c; 109 g[cnt].a=e[i].a; 110 g[cnt].vis=0; 111 } 112 } 113 n=cnt; 114 stack<node>s; 115 s.push(g[1]); 116 if(n>1) s.push(g[2]); 117 for(int i=3;i<=n;i++){ 118 while(s.size()>=2){ 119 node u2=s.top();s.pop(); 120 node u1=s.top(); 121 ll t1=(u1.c-g[i].c)*(u2.a-u1.a); 122 ll t2=(u1.c-u2.c)*(g[i].a-u1.a); 123 if(t1>t2){ 124 s.push(u2); 125 break; 126 } 127 } 128 s.push(g[i]); 129 } 130 int ans=0; 131 while(!s.empty()) 132 { 133 node u=s.top(); 134 s.pop(); 135 if(!u.vis) ans++; 136 } 137 printf("%d ",ans); 138 } 139 return 0; 140 }
E - Lead of Wisdom HDU - 6772
题意:给你n件物品穿戴,每个物品都有四个属性然后有k中物品每种物品只能选一个,求一个式子的最大值。
思路:因为这题数据较小,当时想到暴力搜索,时间复杂度O(316*10*50)进行剪枝就可以了,我们只要定义一个三维数组存s[t][j][k]表示第i中物品的第j个第k个属性。另外需要一个nt数组存该种物品存在的位置,减少不必要的搜索。

1 #include<time.h> 2 #include <set> 3 #include <map> 4 #include <stack> 5 #include <cmath> 6 #include <queue> 7 #include <cstdio> 8 #include <cstring> 9 #include <string> 10 #include <vector> 11 #include <cstring> 12 #include <iostream> 13 #include <algorithm> 14 #include <list> 15 using namespace std; 16 #define eps 1e-10 17 #define PI acos(-1.0) 18 #define lowbit(x) ((x)&(-x)) 19 #define zero(x) (((x)>0?(x):-(x))<eps) 20 #define mem(s,n) memset(s,n,sizeof s); 21 #define ios {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);} 22 typedef long long ll; 23 typedef unsigned long long ull; 24 const int maxn=1e6+5; 25 const int Inf=0x7f7f7f7f; 26 const ll Mod=1e9+7; 27 const int N=3e3+5; 28 bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }//判断一个数是不是 2 的正整数次幂 29 int modPowerOfTwo(int x, int mod) { return x & (mod - 1); }//对 2 的非负整数次幂取模 30 int getBit(int a, int b) { return (a >> b) & 1; }// 获取 a 的第 b 位,最低位编号为 0 31 int Max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }// 如果 a>=b,(a-b)>>31 为 0,否则为 -1 32 int Min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); } 33 ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;} 34 ll lcm(ll a, ll b) {return a / gcd(a, b) * b;} 35 int Abs(int n) { 36 return (n ^ (n >> 31)) - (n >> 31); 37 /* n>>31 取得 n 的符号,若 n 为正数,n>>31 等于 0,若 n 为负数,n>>31 等于 -1 38 若 n 为正数 n^0=n, 数不变,若 n 为负数有 n^(-1) 39 需要计算 n 和 -1 的补码,然后进行异或运算, 40 结果 n 变号并且为 n 的绝对值减 1,再减去 -1 就是绝对值 */ 41 } 42 ll binpow(ll a, ll b,ll c) { 43 ll res = 1; 44 while (b > 0) { 45 if (b & 1) res = res * a%c; 46 a = a * a%c; 47 b >>= 1; 48 } 49 return res%c; 50 } 51 void extend_gcd(ll a,ll b,ll &x,ll &y) 52 { 53 if(b==0) { 54 x=1,y=0; 55 return; 56 } 57 extend_gcd(b,a%b,x,y); 58 ll tmp=x; 59 x=y; 60 y=tmp-(a/b)*y; 61 } 62 ll mod_inverse(ll a,ll m) 63 { 64 ll x,y; 65 extend_gcd(a,m,x,y); 66 return (m+x%m)%m; 67 } 68 ll eulor(ll x) 69 { 70 ll cnt=x; 71 ll ma=sqrt(x); 72 for(int i=2;i<=ma;i++) 73 { 74 if(x%i==0) cnt=cnt/i*(i-1); 75 while(x%i==0) x/=i; 76 } 77 if(x>1) cnt=cnt/x*(x-1); 78 return cnt; 79 } 80 int T,t,n,k,nt[55],num[55],s[55][100][4]; 81 ll Maxx; 82 void dfs(int t,int a,int b,int c,int d) 83 { 84 if(t>k) 85 { 86 ll ans=1ll*a*b*c*d; 87 if(ans>Maxx) Maxx=ans; 88 return ; 89 } 90 if(!num[t]) 91 { 92 dfs(nt[t],a,b,c,d); 93 return ; 94 } 95 for(int i=1;i<=num[t];i++) 96 { 97 dfs(t+1,a+s[t][i][0],b+s[t][i][1],c+s[t][i][2],d+s[t][i][3]); 98 } 99 } 100 int main() 101 { 102 scanf("%d",&T); 103 while(T--) 104 { 105 scanf("%d%d",&n,&k); 106 for(int i=1;i<=k;i++) num[i]=0; 107 for(int i=0;i<n;i++) 108 { 109 scanf("%d",&t); 110 num[t]++; 111 for(int j=0;j<4;j++) 112 { 113 scanf("%d",&s[t][num[t]][j]); 114 } 115 } 116 t=k+1; 117 for(int i=k;i>=1;i--) 118 { 119 nt[i]=t; 120 if(num[i]) t=i; 121 } 122 Maxx=0; 123 dfs(1,100,100,100,100); 124 printf("%lld ",Maxx); 125 } 126 127 }
F - The Oculus HDU - 6768
题意:
定义(F_i)为斐波那契数列第(i)项,(F_1=1, F_2=2, F_i=F_{i-1}+F_{i-2} (i≥3))
已知任意正整数(x)都拥有一个唯一的长度为(n)的(01)数列({b}),使得
(b_1*F_1+b_2*F_2+...+b_n*F_n=x)
(b_n=1)
(b_i∈{0,1})
(b_i*b_{i+1}=0)
以这样的表示法给出(A、B、C)三个数
已知数字(C)是由(A*B)的结果在这样的表示法下将某个原本是(1)的位置改成(0)得来的
问抹去的是哪个位置
思路:只要通过(A*B-C)来计算出被抹去的数对应的数字是什么就好了,前提打表前2000000项斐波那契数列,队友lc直接暴力做就A了,但是要用ull数据类型。看他人博客推荐使用(map/unordered\_map/gp\_hash\_table)存。

1 #include<time.h> 2 #include <set> 3 #include <map> 4 #include <stack> 5 #include <cmath> 6 #include <queue> 7 #include <cstdio> 8 #include <cstring> 9 #include <string> 10 #include <vector> 11 #include <cstring> 12 #include <iostream> 13 #include <algorithm> 14 #include <list> 15 using namespace std; 16 #define eps 1e-10 17 #define PI acos(-1.0) 18 #define lowbit(x) ((x)&(-x)) 19 #define zero(x) (((x)>0?(x):-(x))<eps) 20 #define mem(s,n) memset(s,n,sizeof s); 21 #define ios {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);} 22 typedef long long ll; 23 typedef unsigned long long ull; 24 const int maxn=3e6+5; 25 const int Inf=0x7f7f7f7f; 26 const ll Mod=1e9+7; 27 const int N=3e3+5; 28 bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }//判断一个数是不是 2 的正整数次幂 29 int modPowerOfTwo(int x, int mod) { return x & (mod - 1); }//对 2 的非负整数次幂取模 30 int getBit(int a, int b) { return (a >> b) & 1; }// 获取 a 的第 b 位,最低位编号为 0 31 int Max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }// 如果 a>=b,(a-b)>>31 为 0,否则为 -1 32 int Min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); } 33 ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;} 34 ll lcm(ll a, ll b) {return a / gcd(a, b) * b;} 35 int Abs(int n) { 36 return (n ^ (n >> 31)) - (n >> 31); 37 /* n>>31 取得 n 的符号,若 n 为正数,n>>31 等于 0,若 n 为负数,n>>31 等于 -1 38 若 n 为正数 n^0=n, 数不变,若 n 为负数有 n^(-1) 39 需要计算 n 和 -1 的补码,然后进行异或运算, 40 结果 n 变号并且为 n 的绝对值减 1,再减去 -1 就是绝对值 */ 41 } 42 ll binpow(ll a, ll b,ll c) { 43 ll res = 1; 44 while (b > 0) { 45 if (b & 1) res = res * a%c; 46 a = a * a%c; 47 b >>= 1; 48 } 49 return res%c; 50 } 51 void extend_gcd(ll a,ll b,ll &x,ll &y) 52 { 53 if(b==0) { 54 x=1,y=0; 55 return; 56 } 57 extend_gcd(b,a%b,x,y); 58 ll tmp=x; 59 x=y; 60 y=tmp-(a/b)*y; 61 } 62 ll mod_inverse(ll a,ll m) 63 { 64 ll x,y; 65 extend_gcd(a,m,x,y); 66 return (m+x%m)%m; 67 } 68 ll eulor(ll x) 69 { 70 ll cnt=x; 71 ll ma=sqrt(x); 72 for(int i=2;i<=ma;i++) 73 { 74 if(x%i==0) cnt=cnt/i*(i-1); 75 while(x%i==0) x/=i; 76 } 77 if(x>1) cnt=cnt/x*(x-1); 78 return cnt; 79 } 80 ull f[maxn],a,b,c; 81 int T; 82 void fei() 83 { 84 f[1]=1; 85 f[2]=2; 86 for(int i=3;i<=maxn;i++) 87 f[i]=f[i-1]+f[i-2]; 88 } 89 int main() 90 { 91 scanf("%d",&T); 92 fei(); 93 while(T--) 94 { 95 int k,x; 96 a=b=c=0; 97 scanf("%d",&k); 98 for(int i=1;i<=k;i++) 99 { 100 scanf("%d",&x); 101 a+=f[i]*x; 102 } 103 scanf("%d",&k); 104 for(int i=1;i<=k;i++) 105 { 106 scanf("%d",&x); 107 b+=f[i]*x; 108 } 109 scanf("%d",&k); 110 for(int i=1;i<=k;i++) 111 { 112 scanf("%d",&x); 113 c+=f[i]*x; 114 } 115 c=a*b-c; 116 for(int i=1;i<maxn;i++) 117 { 118 if(f[i]==c) {k=i;break;} 119 } 120 cout<<k<<endl; 121 } 122 }
G - Total Eclipse HDU - 6763
J - Parentheses Matching HDU - 6799
这两题完全没有参与。
第一次组队训练的效果很好,大家状态都很好,希望能一直保持下去,加油加油!
