全排序的理解

    全排序：是对数列所有排列结果的运算，对于一个长度为n的数列来说，它的排列有n!种。

我的理解是从数列的开头进行固定，每次向后固定元素，遍历到结尾的时候代表一种排列的可能，然后返回上一层，切换下一个数字继续深入排序

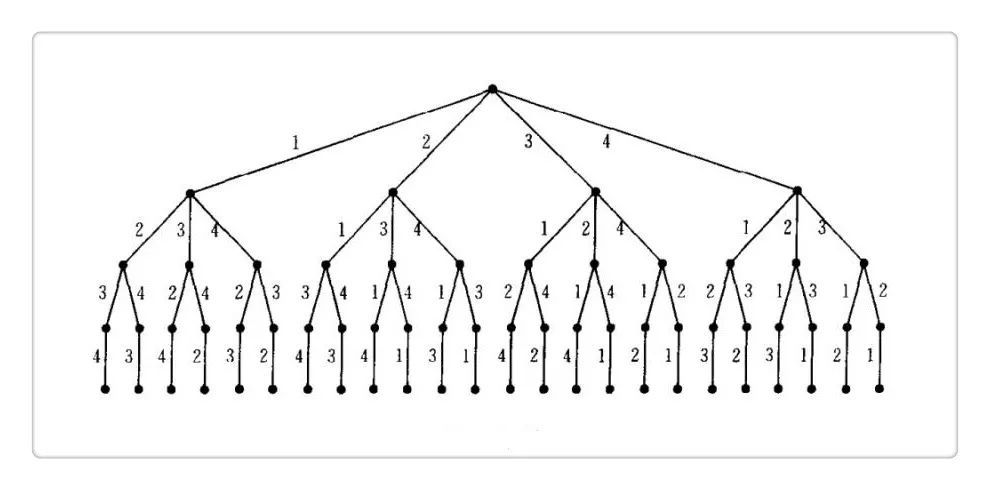
例如： 1 2 3 4 ，固定 1 2  ，最后先以三开头，遍历到结尾打印，返回上一层，以4开头打印，再返回2所在的那一层，分别以 3 4开头进行遍历打印

最后返回到1所在的那层 ，分别切换成2 3 4 开头进行上述遍历

　　

#include<stdio.h>

void swap(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void Perm(int arr[],int lo,int hi)
{
    if (lo == hi)//递归到最深层，打印这次的排列结果,然后返回上一层进行循环，继续交换，继续递归
    {
        for (int j = 0; j <=hi; j++)
        {
            printf("%d", arr[j]);
        }
        printf("
");
    }

    //改良，运算更快，但是打印会慢一点
    //Perm(arr，lo+1,hi);
    /*for (int i = lo+1; i <= hi; i++)
    {
        swap(&arr[i], &arr[lo]);//lo是固定的那个位置，与下一个位置交换。
        Perm(arr, lo + 1, hi);
        swap(&arr[i],&arr[lo]); //恢复先前的交换，防止数列顺序改变
    }*/
    for (int i = lo; i <= hi; i++)
    {
        swap(&arr[i], &arr[lo]);//lo是固定的那个位置，与下一个位置交换。
        Perm(arr, lo + 1, hi);
        swap(&arr[i],&arr[lo]); //恢复先前的交换，防止数列顺序改变
    }


}


int main()
{
    int arr[4] = { 1,2,3 ,4};
    Perm(arr, 0, 3);
    return 0;
}

//改良版
#include<stdio.h>

void swap(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void Perm(int arr[],int lo,int hi)
{
    if (lo == hi)//递归到最深层，打印这次的排列结果,然后返回上一层进行循环，继续交换，继续递归
    {
        for (int j = 0; j <=hi; j++)
        {
            printf("%d", arr[j]);
        }
        printf("
");
    }

    //改良，运算更快，但是打印会慢一点
    Perm(arr，lo+1,hi);
    for (int i = lo+1; i <= hi; i++)
    {
        swap(&arr[i], &arr[lo]);//lo是固定的那个位置，与下一个位置交换。
        Perm(arr, lo + 1, hi);
        swap(&arr[i],&arr[lo]); //恢复先前的交换，防止数列顺序改变
    }
    
}


int main()
{
    int arr[4] = { 1,2,3 ,4};
    Perm(arr, 0, 3);
    return 0;
}