【问题】

【思路】
由于题目是让求出需要翻译机的个数,一共有m个人,并且每个人可能一种语言都不会,也有可能会多种语言!因此,一个很通用的思路我们将可以互相交流的放到一个集合中,最终如果形成n个集合,那么就需要n-1个翻译机!
说到集合的多次合并问题,不得不提一个高效且很容易实现的结构,并查集!并查集的理论首先对一些数据进行初始化节点,使用father_map和size_map表示,初始化时节点的父节点为其本身,我们也叫作代表节点!
合并两个集合时,我们需要判断其代表节点是否相同以及大小,如果相同,属于统一集合,直接return, 否则,将小的集合的代表节点直接挂在大集合的节点上,完成合并!
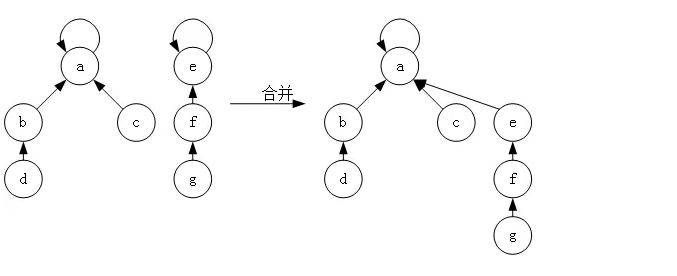
但是,其真正高效的原因是由于查找操作造成的,其查找代表节点的同时,会将其上方的节点全部挂在代表节点上,下次查询时间都为O(1)了!这也是并查集为什么进行多次合并都很高效的主要原因!

针对于本题,主要分为五个步骤:
1. 首先统计每种语言所会的人,count=n(人数),并对每个人建立并查集初始化!
2. 遍历每个语言,将这每个语言对应的人所在的集合进行合并!
3. 每次合并count都要减一, 也就是需要翻译机的个数减一!
4. 所有合并结束后,最后孤立无法交流的集合数为count
5. 因此需要count-1个翻译机
#include <unordered_map> #include <iostream> #include <vector> #include <string> using namespace std; class UnionFindSet { public: int getMachineNum(vector<vector<int>> matrix, int person_num, int language_num, int num) { //num 为人数 if (!matrix.size()) return 0; vector<vector<int>> tmp(language_num); for (int i = 0; i < num; i++) { tmp[matrix[i][1] - 1].push_back(matrix[i][0] - 1); // 每种语言都有哪些人使用, 索引从零开始 } // 输出 for (int i = 0; i < tmp.size(); i++) { cout << "语言类别 " << i + 1 << " 会的人为:"; for (int j = 0; j < tmp[i].size(); j++) { cout << tmp[i][j] + 1 << " "; } cout << endl; } for (int i = 0; i < person_num; i++) { father_map[i] = i; size_map[i] = 1; // 初始化并查集 } count = person_num; // count初始化 // 按照会的语言对人的标号进行划分set,如果一个人会A,B语言,则A和B集的所有人都会在一个集合 for (int i = 0; i < tmp.size(); i++) { if (tmp[i].size() >= 2) { for (int j = 0; j < tmp[i].size() - 1; j++) { Union(tmp[i][j], tmp[i][j + 1]); } } } return count - 1; } int findRep(int i) { int tmp = father_map[i]; if (tmp != i) { tmp = findRep(tmp); } father_map[i] = tmp; return tmp; // 每次查找,就将其上级节点都挂在代表节点上 } void Union(int i, int j) { int p = findRep(i); int q = findRep(j); if (p == q) return; if (size_map[p] < size_map[q]) { father_map[p] = q; size_map[q] += size_map[q]; } else { father_map[q] = p; size_map[p] += size_map[p]; } count--; } private: unordered_map<int, int> father_map; unordered_map<int, int> size_map; int count; }; int main() { int m, n, k; cin >> m >> n >> k; vector<vector<int>> matrix(k, vector<int>(2)); for (int i = 0; i < k; i++) { for (int j = 0; j < 2; j++) { cin >> matrix[i][j]; } } UnionFindSet set; int count = set.getMachineNum(matrix, m, n, k); cout << "res: " << count << endl; system("PAUSE"); return 0; }