【问题】给出一颗n个结点的树,树上每条边的边权都是1,这n个结点中有m个特殊点,请你求出树上距离这m个特殊点距离均不超过d的点的数量,包含特殊点本身。
输入:
输入第一行包含三个正整数,n、m、d分别表示树上有n个结点,其中有m个点是特殊点,d是如题所示的距离。(1<=n、m、d<=50000)
第二行m个整数,表示特殊的点的编号,编号再1-n之间。
第三行有n-1个整数,第个数表示第号结点的父亲结点的编号,同样在1-n之间。
输出:
输出仅包含一个整数,即符合题目要求的点的数量。
样例输入:
6 2 3
2 1
3 4 5 6 1
样例输出:
2
首先题目给出了说明,这棵树一共有n个节点,且边的权重为1,并且有m个特殊节点,虽然题目说了这是一个树,但是要求是找到距离m个特殊节点"均"不超过d的节点,因此如果从某一个特殊节点出发,它既可以向上查找,也可以向下查找,这明明就是一个图,题目忽悠人的好不!!!
其实想通了思路就很清晰了,首先我们建立邻接表,题目给出的节点标号是1~N,由于数组的索引从零开始,因此建立邻接表的时候要对节点标号做一个减一的操作!因为我们使用了动态数组vector,因此对于没有连接的两个节点,我们就不添加元素(并不是设置为权重为零)!还有一点需要注意:自身与自身的节点也是相连的,需要添加进去!(题目说包含特殊节点本身)
// 创建邻接表 for (int i = 0; i < list.size();i++) { neigbor[i+1].push_back(list[i] - 1); neigbor[list[i] - 1].push_back(i+1); } for (int i = 0; i < neigbor.size(); i++) { neigbor[i].push_back(i); }
接着我们遍历特殊节点,然后使用bfs算法来进行广度搜索,用dis变量来标记距离,如果距离大于d,就不再搜索,跳出循环!注意我们在进行广度搜索的时候要一次性处理一层节点!这也是while(size--)的作用,这种做法很类似于"之字形打印数组"。对于一个特殊节点,我们在dis变量的限制下尽可能的去搜索符合条件的节点,使用set用来判断是否访问过该节点,然后将flag中对应的节点进行自加操作!换句话说,一个特殊节点进行广度搜索时,flag数组的值最多只会加一次或者不加!
此时,flag数组表示对于某一个特殊节点,符合要求的节点有哪些(包含特殊节点本身),接着,我们用这个思路遍历每一个特殊节点就可以了!
如果特殊节点有N个,那么flag数组中值为N的标号就是满足条件的节点!也就是距离每个特殊节点距离均小于d。当然题目让返回满足条件的个数,那就数一下值为N的节点个数就行了!!!
#include <iostream> #include <vector> #include <queue> #include <unordered_set> using namespace std; int main() { int n, m, d; cin >> n >> m >> d; vector<vector<int>> neigbor(n); vector<int> sp(m); vector<int> list(n - 1); for (int i = 0; i < m; i++) { cin >> sp[i]; } for (int i = 0; i < n - 1; i++) { cin >> list[i]; } // 创建邻接表 for (int i = 0; i < list.size();i++) { neigbor[i+1].push_back(list[i] - 1); neigbor[list[i] - 1].push_back(i+1); } for (int i = 0; i < neigbor.size(); i++) { neigbor[i].push_back(i); } // 输出邻接表 cout << "创建邻接表,索引从0开始,题目中编号从1开始,需要注意!" << endl; for (int i = 0; i < neigbor.size(); i++) { for (int j = 0; j < neigbor[i].size(); j++) { cout << neigbor[i][j] << " "; } cout << endl; } vector<int> flag(n, 0); for (int i = 0; i < m; i++) { int dis = 1; queue<int> que; unordered_set<int> set; que.push(sp[i] - 1); // set不需要添加,由于特殊节点本身也需要访问 while (!que.empty()) { int size = que.size(); while (size--) { // 类似于之字形打印二叉树,直接处理一层 int tmp = que.front(); que.pop(); for (int j = 0; j < neigbor[tmp].size(); j++) { if (set.find(neigbor[tmp][j]) == set.end()) { set.insert(neigbor[tmp][j]); flag[neigbor[tmp][j]]++; cout << neigbor[tmp][j] << " ! "; // 输出满足与某一个特殊点距离不大于d的数 } } for (auto i : neigbor[tmp]) { que.push(i); } } dis++; // 距离加一 if (dis > d) { break; } } } int count = 0; for (int i = 0; i < flag.size(); i++) { if (flag[i] == m) { count++; } } cout << endl; cout << "特殊点与那些数相近: "; // 题目要求是特殊点与某些点 (均) 小于d for (auto i : flag) { cout << i << " "; } cout << endl; cout << count << endl; // 输出 system("PAUSE"); return 0; }
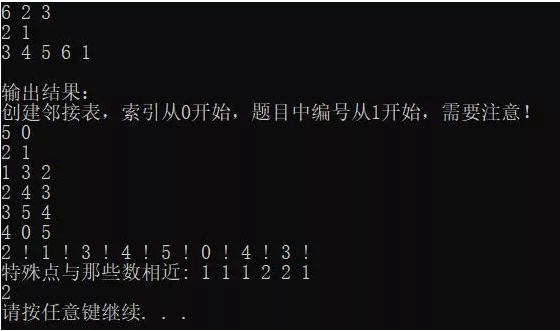
输出结果分析:
由于题中样例构建出来的树为:(注意这里索引从零开始)
1 -> 2 -> 3 -> 4 -> 5 -> 0
所以对于特殊节点1和0来说:
距离1小于d=3的有:1,2,3,4
距离0小于d=3的有:0,5,4,3
所以我们程序中flag数组应该是[1,1,1,2,2,1], 从而符合题目要求的是3和4节点!!!运行结果也表明我们的思路和程序是对的!
从5 0到4 0 5表示我们所创建的邻接表(neigbor)