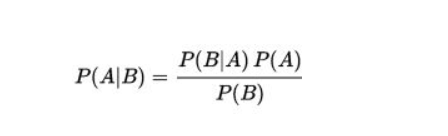☆本周视频学习内容:https://www.bilibili.com/video/BV1Tb411H7uC?p=2
☆本周作业要求:
1)贴上视频学习笔记,要求真实,不要抄袭,可以手写拍照。
解析:
1)P2 概率论与贝叶斯先验

主要学习内容:第3页
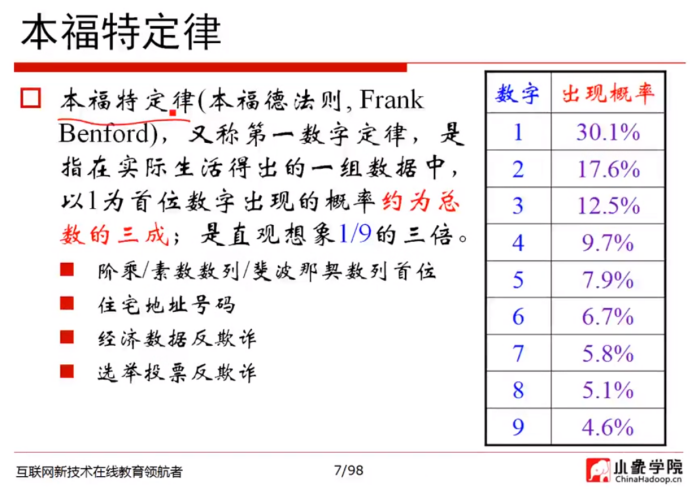
本福特定律:第7页
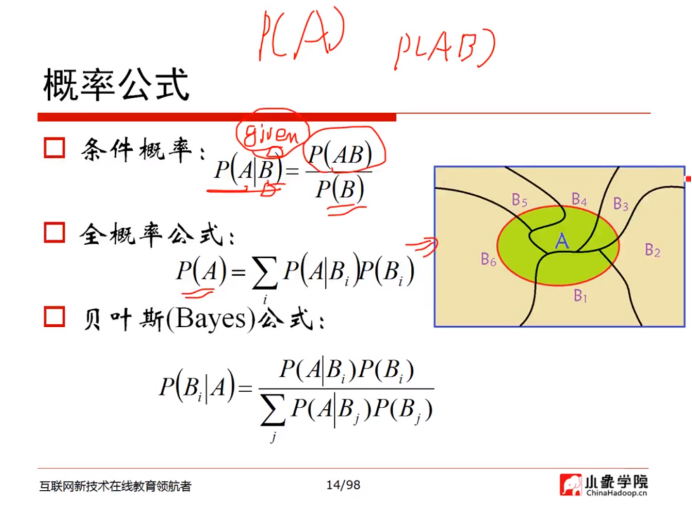
概率公式:第14页

贝叶斯公式的应用:第16页

贝叶斯公式:第17页
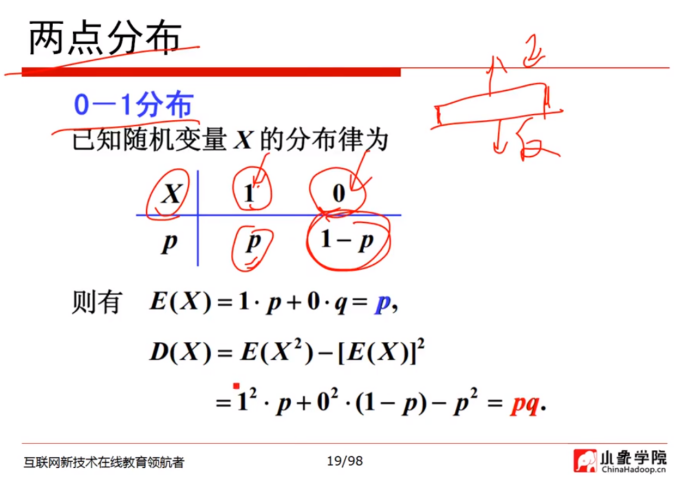
两点分步:第19页

二项分布:第20页

泊松分布:第24页

均匀分布:第27页

指数分布:第28页

正态分布:第31页
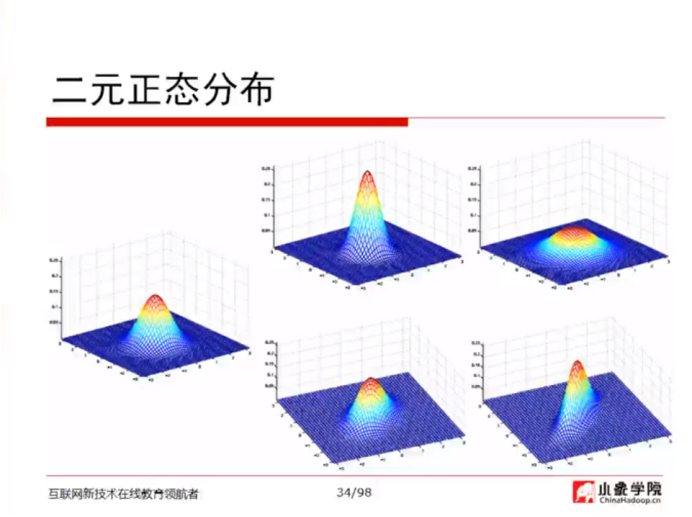
二元正态分布:第34页

各项分布的知识总结:第35页

Beta分布:第36页
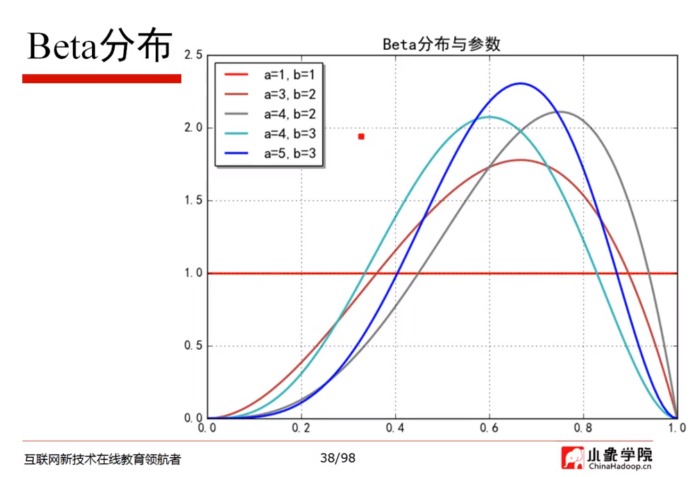
Beta分布图:第38页

事件独立性:第46页

方差:第57页

协方差:第58页

协方差矩阵:第68页

切比雪夫不等式:第72页

伯努利定理:第77页

中心极限定理:第78页

贝叶斯公式思考题:第83页
2)P3 矩阵和线性代数
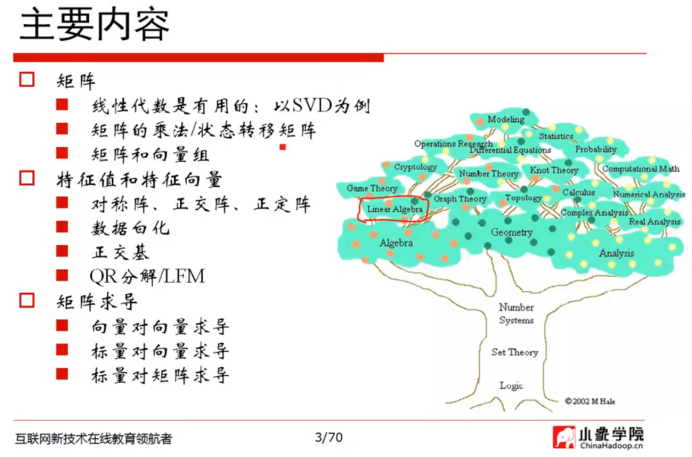
主要学习内容:第3页

线性代数定义:第9页

代数余子式:第12页

系数矩阵:第32页
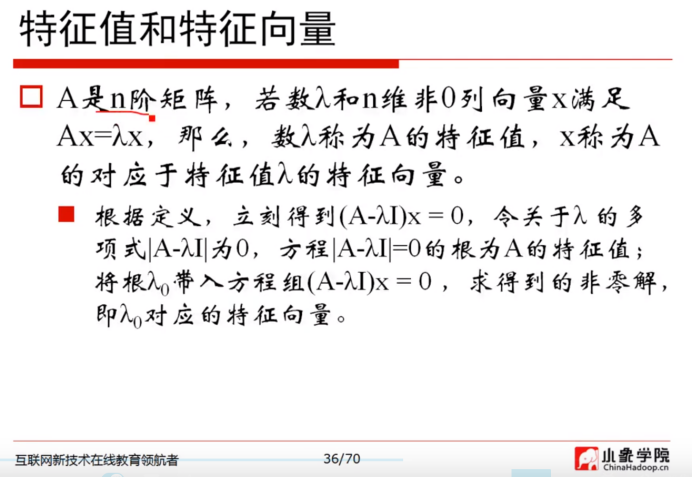
特征值和特征向量:第36页

思考总结:第67页
2)用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”,可以word编辑,可做思维导图,可以手写拍照,要求言简意赅、排版整洁。
解析:
梯度:我对梯度的直观理解是,梯度的本意是一个向量,表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向变化最快,变化率最大。也就是说:梯度可以定义为一个函数的全部偏导数构成的向量。
梯度下降:主要目的是通过不断地迭代来寻找到目标函数的最小值,或者收敛到最小值。
贝叶斯定理:贝叶斯定理是关于随机事件A和B的条件概率的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。数学公式如下: