基本数据Tensor可以保证完成前向传播, 想要完成神经网络的训练, 接下来还需要进行反向传播与梯度更新, 而PyTorch提供了自动求导机制autograd, 将前向传播的计算记录成计算图, 自动完成求导。在PyTorch 0.4版本之前, Tensor仅仅是对多维数组的抽象, 使用自动求导机制需要将Tensor封装成torch.autograd.Variable类型, 才能构建计算图。 PyTorch 0.4版本则将Tensor与Variable进行了整合, 以前Variable的使用情景都可以直接使用Tensor, 变得更简单实用。
本节首先介绍Tensor的自动求导属性, 然后对计算图进行简要的讲解。
1. Tensor的自动求导: Autograd
自动求导机制记录了Tensor的操作, 以便自动求导与反向传播。 可以通过requires_grad参数来创建支持自动求导机制的Tensor。
require_grad参数表示是否需要对该Tensor进行求导, 默认为False;设置为True则需要求导, 并且依赖于该Tensor的之后的所有节点都需要求导。 值得注意的是, 在PyTorch 0.4对于Tensor的自动求导中, volatile参数已经被其他torch.no_grad()等函数取代了。
Tensor有两个重要的属性, 分别记录了该Tensor的梯度与经历的操作。
grad: 该Tensor对应的梯度, 类型为Tensor, 并与Tensor同维度。
grad_fn: 指向function对象, 即该Tensor经过了什么样的操作, 用作反向传播的梯度计算, 如果该Tensor由用户自己创建, 则该grad_fn为None。
具体的参数使用示例如下:

1 import torch 2 3 a = torch.randn(2, 2, requires_grad=True) 4 b = torch.randn(2, 2) 5 6 # 可以看到默认的Tensor是不需要求导的, 设置requires_grad为True后则需要求导 7 print(a.requires_grad) 8 >> True 9 print(b.requires_grad) 10 >> False 11 12 # 也可以通过内置函数requires_grad_()将Tensor变为需要求导 13 print(b.requires_grad_()) 14 >> tensor([[ 1.3655, -1.5378], 15 [-0.2241, -1.4778]], requires_grad=True) 16 print(b.requires_grad) 17 >> True 18 19 # 通过计算生成的Tensor, 由于依赖的Tensor需要求导, 因此c也需要求导 20 c = a + b 21 print(c.requires_grad) 22 >> True 23 24 # a与b是自己创建的, grad_fn为None, 而c的grad_fn则是一个Add函数操作 25 print(a.grad_fn, b.grad_fn, c.grad_fn) 26 >> None None <AddBackward0 object at 0x7f5ae5a45390> 27 # detach就是截断反向传播的梯度流 28 d = c.detach() 29 print(d.requires_grad) 30 >> False
注意: 早些版本使用.data属性来获取数据, PyTorch 0.4中建议使用Tensor.detach()函数, 因为.data属性在某些情况下不安全, 原因在于对.data生成的数据进行修改不会被autograd追踪。 Tensor.detach()函数生成的数据默认requires_grad为False。
2. 计算图
计算图是PyTorch对于神经网络的具体实现形式, 包括每一个数据Tensor及Tensor之间的函数function。 在此我们以z=wx+b为例, 通常在神经网络中, x为输入, w与b为网络需要学习的参数, z为输出, 在这一层, 计算图构建方法如图2.4所示。 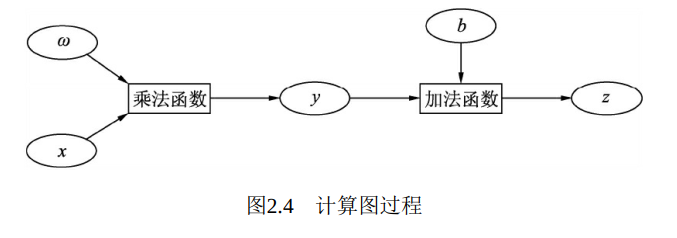
在图2.4中, x、 ω和b都是用户自己创建的, 因此都为叶节点, ωx首先经过乘法算子产生中间节点y, 然后与b经过加法算法产生最终输出z, 并作为根节点。
Autograd的基本原理是随着每一步Tensor的计算操作, 逐渐生成计算图, 并将操作的function记录在Tensor的grad_fn中。 在前向计算完后, 只需对根节点进行backward函数操作, 即可从当前根节点自动进行反向传播与梯度计算, 从而得到每一个叶子节点的梯度, 梯度计算遵循链式求导法则。

1 import torch 2 3 # 生成3个Tensor变量, 并作为叶节点 4 x = torch.randn(1) 5 w = torch.ones(1, requires_grad =True) 6 b = torch.ones(1, requires_grad=True) 7 8 # 自己生成的, 因此都为叶节点 9 print(x.is_leaf, w.is_leaf, b.is_leaf) 10 >> True True True 11 12 # 进行前向计算, 由计算生成的变量都不是叶节点 13 y = w*x 14 z = y+b 15 print(y.is_leaf, z.is_leaf) 16 >> False False 17 18 # 由于依赖的变量有需要求导的, 因此y与z都需要求导 19 print(y.requires_grad, z.requires_grad) 20 >> True True 21 22 23 # grad_fn记录生成该变量经过了什么操作, 如y是Mul, z是Add 24 print(y.grad_fn, z.grad_fn) 25 >> <MulBackward0 object at 0x7fb2cff0d390> <AddBackward0 object at 0x7fb2cff0d3c8> 26 27 # 对根节点调用backward()函数, 进行梯度反传 28 z.backward(retain_graph =True) 29 print(w.grad, b.grad) 30 >> tensor([0.1494]) tensor([1.])
3. Autograd注意事项
PyTorch的Autograd机制使得其可以灵活地进行前向传播与梯度计算, 在实际使用时, 需要注意以下3点, 如图2.5所示。
动态图特性: PyTorch建立的计算图是动态的, 这也是PyTorch的一大特点。 动态图是指程序运行时, 每次前向传播时从头开始构建计算图, 这样不同的前向传播就可以有不同的计算图, 也可以在前向时插入各种Python的控制语句, 不需要事先把所有的图都构建出来, 并且可以很方便地查看中间过程变量。
backward()函数还有一个需要传入的参数grad_variabels, 其代表了根节点的导数, 也可以看做根节点各部分的权重系数。 因为PyTorch不允许Tensor对Tensor求导, 求导时都是标量对于Tensor进行求导, 因此, 如果根节点是向量, 则应配以对应大小的权重, 并求和得到标量,再反传。 如果根节点的值是标量, 则该参数可以省略, 默认为1。
当有多个输出需要同时进行梯度反传时, 需要将retain_graph设置为True, 从而保证在计算多个输出的梯度时互不影响。
