1. 索引操作与NumPy非常类似, 主要包含下标索引、 表达式索引、 使用torch.where()与Tensor.clamp()的选择性索引。

1 import torch 2 3 a = torch.Tensor([[0,1],[2,3]]) 4 print(a, a.size()) 5 >> tensor([[0., 1.], 6 [2., 3.]]) torch.Size([2, 2]) 7 8 # 根据下标进行索引 9 print(a[1]) 10 >> tensor([2., 3.]) 11 print(a[0,1]) 12 >> tensor(1.) 13 14 # 选择a中大于0的元素, 返回和a相同大小的Tensor, 符合条件的置1, 否则置0 15 b = a>0 16 print(b) 17 >> tensor([[False, True], 18 [ True, True]]) 19 20 # 选择符合条件的元素并返回, 等价于torch.masked_select(a, a>0) 21 c= a[a>0] 22 print(c) 23 >> tensor([1., 2., 3.]) 24 25 # 选择非0元素的坐标, 并返回 26 d = torch.nonzero(a) 27 print(d) 28 >> tensor([[0, 1], 29 [1, 0], 30 [1, 1]]) 31 32 # torch.where(condition, x, y), 满足condition的位置输出x, 否则输出y 33 e = torch.where(a>1, torch.full_like(a,1), a) 34 print(e) 35 >> tensor([[0., 1.], 36 [1., 1.]]) 37 38 # 对Tensor元素进行限制可以使用clamp()函数, 示例如下, 限制最小值为1, 最大值为2 39 f = a.clamp(1, 2) 40 print(f) 41 >> tensor([[1., 1.], 42 [2., 2.]])
2. 变形操作则是指改变Tensor的维度, 以适应在深度学习的计算中,数据维度经常变换的需求, 是一种十分重要的操作。 在PyTorch中主要有4类不同的变形方法, 如表2.2所示。 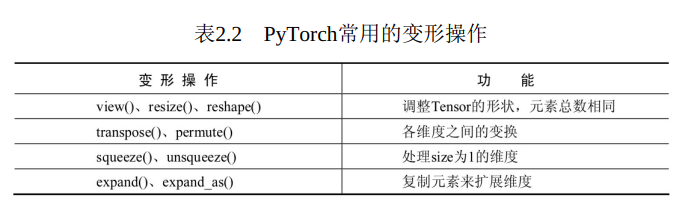
2.1 view()、 resize()和reshape()函数
view()、 resize()和reshape()函数可以在不改变Tensor数据的前提下任意改变Tensor的形状, 必须保证调整前后的元素总数相同, 并且调整前后共享内存, 三者的作用基本相同。

1 import torch 2 3 a = torch.arange(1,5) 4 print(a, a.size()) 5 >> tensor([1, 2, 3, 4]) torch.Size([4]) 6 7 # 分别使用view()、 resize()及reshape()函数进行维度变换 8 b = a.view(2,2) 9 print(b, b.size()) 10 >> tensor([[1, 2], 11 [3, 4]]) torch.Size([2, 2]) 12 13 c = a.resize(4,1) 14 print(c, c.size()) 15 >> tensor([[1], 16 [2], 17 [3], 18 [4]]) torch.Size([4, 1]) 19 20 d = a.reshape(4,1) 21 print(d, d.shape) 22 >> tensor([[1], 23 [2], 24 [3], 25 [4]]) torch.Size([4, 1]) 26 27 # 改变了b、 c、 d的一个元素, a也跟着改变了, 说明两者共享内存 28 b[0,0]=5 29 c[1,0]=6 30 d[2,0]=8 31 print(a, a.size()) 32 >> tensor([5, 6, 8, 4]) torch.Size([4])
如果想要直接改变Tensor的尺寸, 可以使用resize_()的原地操作函数。 在resize_()函数中, 如果超过了原Tensor的大小则重新分配内存,多出部分置0, 如果小于原Tensor大小则剩余的部分仍然会隐藏保留。

1 import torch 2 3 a = torch.arange(1,5) 4 print(a, a.size()) 5 >> tensor([1, 2, 3, 4]) torch.Size([4]) 6 7 c = a.resize_(2, 3) 8 print(c, c.shape) 9 >> tensor([[ 1, 2, 3], 10 [ 4, 8390891550144357996, 2338328219312204072]]) torch.Size([2, 3]) 11 12 # 发现操作后a也跟着改变了 13 print(a, a.size()) 14 >> tensor([[ 1, 2, 3], 15 [ 4, 8390891550144357996, 2338328219312204072]]) torch.Size([2, 3])
2.2 transpose()和permute()函数
transpose()函数可以将指定的两个维度的元素进行转置, 而permute()函数则可以按照给定的维度进行维度变换。

1 import torch 2 3 a = torch.randn(2,2,2) 4 print(a, a.size()) 5 >> tensor([[[ 0.9869, -2.1322], 6 [-0.3327, -1.3120]], 7 8 [[-1.8242, 0.2739], 9 [ 0.4190, -0.8228]]]) torch.Size([2, 2, 2]) 10 11 # 将第0维和第1维的元素进行转置 12 b = a.transpose(0, 1) 13 print(b, b.size()) 14 >> tensor([[[ 0.9869, -2.1322], 15 [-1.8242, 0.2739]], 16 17 [[-0.3327, -1.3120], 18 [ 0.4190, -0.8228]]]) torch.Size([2, 2, 2]) 19 20 # 按照第2、 1、 0的维度顺序重新进行元素排列 21 c = a.permute(2, 1, 0) 22 print(c, c.size()) 23 >> tensor([[[ 0.9869, -1.8242], 24 [-0.3327, 0.4190]], 25 26 [[-2.1322, 0.2739], 27 [-1.3120, -0.8228]]]) torch.Size([2, 2, 2])
transpose的维度及转换理解,参考:https://blog.csdn.net/ldm_666/article/details/107183244
2.3 squeeze()和unsqueeze()函数
在实际的应用中, 经常需要增加或减少Tensor的维度, 尤其是维度为1的情况, 这时候可以使用squeeze()与unsqueeze()函数, 前者用于去除size为1的维度, 而后者则是将指定的维度的size变为1。

1 import torch 2 3 a = torch.arange(1, 5) 4 print(a, a.shape) 5 >> tensor([1, 2, 3, 4]) torch.Size([4]) 6 7 b = a.reshape(2, 2) 8 print(b, b.shape) 9 >> tensor([[1, 2], 10 [3, 4]]) torch.Size([2, 2]) 11 12 # 将第0维变为1, 因此总的维度为1*3 13 d = b.unsqueeze(0).shape 14 print(d) 15 >> torch.Size([1, 2, 2]) 16 17 f = b.squeeze(0).shape 18 print(f) 19 >> torch.Size([2, 2]) 20 21 # 第0维如果是1, 则去掉该维度, 如果不是1则不起任何作用 22 e = b.unsqueeze(0).squeeze(0).shape 23 print(e) 24 >> torch.Size([2, 2])
2.4 expand()和expand_as()函数
有时需要采用复制元素的形式来扩展Tensor的维度, 这时expand就派上用场了。 expand()函数将size为1的维度复制扩展为指定大小, 也可以使用expand_as()函数指定为示例Tensor的维度

1 import torch 2 3 a = torch.randn(2, 2, 1) 4 print(a, a.shape) 5 >> tensor([[[ 1.0246], 6 [ 1.0175]], 7 8 [[-0.8530], 9 [ 1.4800]]]) torch.Size([2, 2, 1]) 10 11 # 将第2维的维度由1变为3, 则复制该维的元素, 并扩展为3 12 b = a.expand(2, 2, 3) 13 print(b, b.size()) 14 >> tensor([[[ 1.0246, 1.0246, 1.0246], 15 [ 1.0175, 1.0175, 1.0175]], 16 17 [[-0.8530, -0.8530, -0.8530], 18 [ 1.4800, 1.4800, 1.4800]]]) torch.Size([2, 2, 3])
注意: 在进行Tensor操作时, 有些操作如transpose()、 permute()等可能会把Tensor在内存中变得不连续, 而有些操作如view()等是需要Tensor内存连续的, 这种情况下需要使用contiguous()操作先将内存变为 连续的。 在PyTorch v0.4版本中增加了reshape()操作, 可以看做是Tensor.contiguous().view()。
2.5 Tensor的排序与取极值
比较重要的是排序函数sort(), 选择沿着指定维度进行排序, 返回排序后的Tensor及对应的索引位置。 max()与min()函数则是沿着指定维度选择最大与最小元素, 返回该元素及对应的索引位置

1 import torch 2 3 a = torch.randn(3, 3) 4 print(a, a.size()) 5 >> tensor([[-1.8310, 0.2018, -0.3047], 6 [-0.0779, 0.6070, 1.3419], 7 [ 0.8848, -0.7372, -0.6949]]) torch.Size([3, 3]) 8 9 # 按照第0维即按行排序, 每一列进行比较, True代表降序, False代表升序 10 b = a.sort(0, True)[0] 11 print(b) 12 >> tensor([[ 0.8848, 0.6070, 1.3419], 13 [-0.0779, 0.2018, -0.3047], 14 [-1.8310, -0.7372, -0.6949]]) 15 16 c = a.sort(0, True)[1] #输出的下标 17 print(c) 18 >> tensor([[2, 1, 1], 19 [1, 0, 0], 20 [0, 2, 2]]) 21 22 # 按照第1维即按列排序, 每一行进行比较, True代表降序, False代表升序 23 d = a.sort(1, True)[0] 24 print(d) 25 >> tensor([[ 0.2018, -0.3047, -1.8310], 26 [ 1.3419, 0.6070, -0.0779], 27 [ 0.8848, -0.6949, -0.7372]]) 28 29 e = a.sort(1, True)[1] 30 print(e) 31 >> tensor([[1, 2, 0], 32 [2, 1, 0], 33 [0, 2, 1]]) 34 35 # 按照第0维即按行选取最大值, 即将每一列的最大值选取出来 36 f = a.max(0) 37 print(f) 38 >> torch.return_types.max( 39 values=tensor([0.8848, 0.6070, 1.3419]), 40 indices=tensor([2, 1, 1]))
对于Tensor的单元素数学运算, 如abs()、 sqrt()、 log()、 pow()和三角函数等, 都是逐元素操作(element-wise) , 输出的Tensor形状与原始Tensor形状一致。
对于类似求和、 求均值、 求方差、 求距离等需要多个元素完成的操作, 往往需要沿着某个维度进行计算, 在Tensor中属于归并操作, 输出形状小于输入形状。 由于比较简单且与NumPy极为相似, 在此就不详细展开。
2.6 Tensor的自动广播机制与向量化
PyTorch在0.2版本以后, 推出了自动广播语义, 即不同形状的Tensor进行计算时, 可自动扩展到较大的相同形状, 再进行计算。 广播机制的前提是任一个Tensor至少有一个维度, 且从尾部遍历Tensor维度时, 两者维度必须相等, 其中一个要么是1要么不存在。

1 import torch 2 3 a = torch.ones(3, 1, 2) 4 b = torch.ones(2, 1) 5 6 print(a, a.size()) 7 >> tensor([[[1., 1.]], 8 9 [[1., 1.]], 10 11 [[1., 1.]]]) torch.Size([3, 1, 2]) 12 13 print(b, b.size()) 14 >> tensor([[1.], 15 [1.]]) torch.Size([2, 1]) 16 17 # 从尾部遍历维度, 1对应2, 2对应1, 3对应不存在, 因此满足广播条件, 最后求和后的维度为[3,2,2] 18 c = a+b 19 print(c, c.shape) 20 >> tensor([[[2., 2.], 21 [2., 2.]], 22 23 [[2., 2.], 24 [2., 2.]], 25 26 [[2., 2.], 27 [2., 2.]]]) torch.Size([3, 2, 2]) 28 29 30 # a与c最后一维的维度为2对应3, 不满足广播条件, 因此报错 31 d = torch.ones(2, 3) 32 f = a+d 33 print(f.size()) 34 >> 发生异常: RuntimeError 35 The size of tensor a (2) must match the size of tensor b (3) at non-singleton dimension 2 36 File "/home/peng/python_pytorch/pytorch_01.py", line 16, in <module> 37 f = a+d
向量化操作是指可以在同一时间进行批量地并行计算, 例如矩阵运算, 以达到更好的计算效率的一种方式。 在实际使用时, 应尽量使用向量化直接对Tensor操作, 避免低效率的for循环对元素逐个操作, 尤其是在训练网络模型时, 如果有大量的for循环, 会极大地影响训练的速度。
2.7 Tensor的内存共享
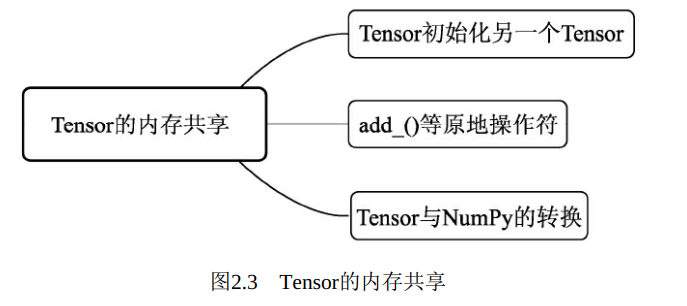
为了实现高效计算, PyTorch提供了一些原地操作运算, 即in-place operation, 不经过复制, 直接在原来的内存上进行计算。 对于内存的共享, 主要有如下3种情况, 如图2.3所示
1) 通过Tensor初始化Tensor
直接通过Tensor来初始化另一个Tensor, 或者通过Tensor的组合、分块、 索引、 变形操作来初始化另一个Tensor, 则这两个Tensor共享内存

1 import torch 2 3 a = torch.randn(2, 2) 4 print(a, a.size()) 5 >> tensor([[ 1.6628, 0.5907], 6 [ 0.8803, -0.5747]]) torch.Size([2, 2]) 7 8 # 用a初始化b, 或者用a的变形操作初始化c, 这三者共享内存, 一个变, 其余的也改变了 9 b = a 10 print(b, b.size()) 11 >> tensor([[ 1.6628, 0.5907], 12 [ 0.8803, -0.5747]]) torch.Size([2, 2]) 13 14 c = a.view(4) 15 print(c, c.size()) 16 >> tensor([ 1.6628, 0.5907, 0.8803, -0.5747]) torch.Size([4]) 17 18 print(a, a.size()) 19 >> tensor([[ 1.6628, 0.5907], 20 [ 0.8803, -0.5747]]) torch.Size([2, 2]) 21 22 print(b, b.size()) 23 >> tensor([[ 1.6628, 0.5907], 24 [ 0.8803, -0.5747]]) torch.Size([2, 2]) 25 26 b[0,0] =0 27 c[3] = 1223 28 print(a, a.size()) 29 >> tensor([[0.0000e+00, 5.9068e-01], 30 [8.8033e-01, 1.2230e+03]]) torch.Size([2, 2]) 31 32 print(c, c.size()) 33 >> tensor([0.0000e+00, 5.9068e-01, 8.8033e-01, 1.2230e+03]) torch.Size([4]) 34 35 print(b, b.size()) 36 >> tensor([[0.0000e+00, 5.9068e-01], 37 [8.8033e-01, 1.2230e+03]]) torch.Size([2, 2])
2)原地操作符
PyTorch对于一些操作通过加后缀“_”实现了原地操作, 如add_()和resize_()等, 这种操作只要被执行, 本身的Tensor则会被改变。

1 import torch 2 3 a = torch.Tensor([[1,2], [3,4]]) 4 print(a, a.size()) 5 >> tensor([[1., 2.], 6 [3., 4.]]) torch.Size([2, 2]) 7 8 # add_()函数使得a也改变了 9 b = a.add_(a) 10 print(a, a.shape) 11 >> tensor([[2., 4.], 12 [6., 8.]]) torch.Size([2, 2]) 13 14 print(b, b.size()) 15 >> tensor([[2., 4.], 16 [6., 8.]]) torch.Size([2, 2]) 17 18 # resize_()函数使得a也发生了改变 19 c = a.resize_(4) 20 print(a, a.size()) 21 >> tensor([2., 4., 6., 8.]) torch.Size([4]) 22 print(c, c.size()) 23 >> tensor([2., 4., 6., 8.]) torch.Size([4])
3)Tensor与NumPy转换
Tensor与NumPy可以高效地进行转换, 并且转换前后的变量共享内存。 在进行PyTorch不支持的操作时, 甚至可以曲线救国, 将Tensor转换为NumPy类型, 操作后再转为Tensor。

1 import torch 2 import numpy as np 3 4 a = torch.rand(1, 2) 5 print(a, a.shape) 6 >> tensor([[0.2477, 0.5157]]) torch.Size([1, 2]) 7 8 # Tensor转为NumPy 9 b = a.numpy() 10 print(b, b.shape) 11 >> [[0.24766904 0.5157364 ]] (1, 2) 12 13 # NumPy转为Tensor 14 c = torch.from_numpy(b) 15 print(c, c.size()) 16 >> tensor([[0.2477, 0.5157]]) torch.Size([1, 2]) 17 18 #Tensor转为list 19 d = a.tolist() 20 print(d) 21 >> [[0.2476690411567688, 0.5157364010810852]]
