20182301 2019-2020-1 《数据结构与面向对象程序设计》第8周学习总结
教材学习内容总结
第十三章
查找
- 线性查找:依次将每个值进行查找
- Comparable 接口允许多态实现算法,而不是只应用于特定的类
while (result == null&&index<data.length){
if (data[index].compareTo(target)==0)
result=data[index];
index++;
}
- 二分查找
Comparable result = null;
int first = 0 ,last = data.length-1
while( result ==null && first <=last){
mid =(first + last)/2;
if(data[mid].compareTo(target)==0)
result=data[mid];
else
if(data[mid].compareTo(target)>0)
last = mid-1;
else
first = mid+1;
}
排序
- 选择排序
void SelectSort(int a[],int n) //选择排序
{
int mix,temp;
for(int i=0;i<n-1;i++) //每次循环数组,找出最小的元素,放在前面,前面的即为排序好的
{
mix=i; //假设最小元素的下标
for(int j=i+1;j<n;j++) //将上面假设的最小元素与数组比较,交换出最小的元素的下标
if(a[j]<a[mix])
mix=j;
//若数组中真的有比假设的元素还小,就交换
if(i!=mix)
{
temp=a[i];
a[i]=a[mix];
a[mix]=temp;
}
}
}
- 插入排序
public Integer[] sort(Integer[] a) {
// TODO Auto-generated method stub
print("init",a);
Integer temp = 0;
for(int i=1;i<a.length;i++) {
//只能从当前索引往前循环,因为索引前的数组皆为有序的,索引只要确定当前索引的数据的为止即可
for(int j=i;j>0 && a[j] < a[j-1];j--) {
temp = a[j];
a[j] = a[j-1];
a[j-1] = temp;
}
print(i +"",a);
}
print("result",a);
return a;
}
- 冒泡排序
public void bubbleSort(Integer[] arr, int n) {
if (n <= 1) return; //如果只有一个元素就不用排序了
for (int i = 0; i < n; ++i) {
// 提前退出冒泡循环的标志位,即一次比较中没有交换任何元素,这个数组就已经是有序的了
boolean flag = false;
for (int j = 0; j < n - i - 1; ++j) { //此处你可能会疑问的j<n-i-1,因为冒泡是把每轮循环中较大的数飘到后面,
// 数组下标又是从0开始的,i下标后面已经排序的个数就得多减1,总结就是i增多少,j的循环位置减多少
if (arr[j] > arr[j + 1]) { //即这两个相邻的数是逆序的,交换
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = true;
}
}
if (!flag) break;//没有数据交换,数组已经有序,退出排序
}
- 快速排序
public static void quickSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>high){
return; }
i=low;
j=high;
//temp就是基准位
temp = arr[low];
while (i<j) {
//先看右边,依次往左递减
while (temp<=arr[j]&&i<j) {
j--;
}
//再看左边,依次往右递增
while (temp>=arr[i]&&i<j) {
i++;
}
//如果满足条件则交换
if (i<j) {
t = arr[j];
arr[j] = arr[i];
arr[i] = t; }
}
//最后将基准为与i和j相等位置的数字交换
arr[low] = arr[i];
arr[i] = temp;
//递归调用左半数组
quickSort(arr, low, j-1);
//递归调用右半数组
quickSort(arr, j+1, high);
}
- 归并排序
public static int[] sort(int[] a,int low,int high){
int mid = (low+high)/2;
if(low<high){
sort(a,low,mid);
sort(a,mid+1,high);
//左右归并
merge(a,low,mid,high);
}
return a;
}
public static void merge(int[] a, int low, int mid, int high) {
int[] temp = new int[high-low+1];
int i= low;
int j = mid+1;
int k=0;
// 把较小的数先移到新数组中
while(i<=mid && j<=high){
if(a[i]<a[j]){
temp[k++] = a[i++];
}else{
temp[k++] = a[j++];
}
}
// 把左边剩余的数移入数组
while(i<=mid){
temp[k++] = a[i++];
}
// 把右边边剩余的数移入数组
while(j<=high){
temp[k++] = a[j++];
}
// 把新数组中的数覆盖nums数组
for(int x=0;x<temp.length;x++){
a[x+low] = temp[x];
}
}
分析查找及排序算法
- 二分查找对数阶的复杂度,对大的查找池来说,这非常有效率
- 选择、插入、冒泡排序的平均运算时间复杂度是O(n^2)
- 快速排序的关键在于选择一个好的划分元素
- 归并排序的最差运算时间复杂度是O(nlogn)
教材学习中的问题和解决过程
- 问题1:归并排序基本了解,但并不是很透彻,于是以下图解:
- 问题1解决方案:(详见链接五)


- 问题2:快速排序基本了解,但并不是很透彻,于是以下图解:
- 问题2解决方案:(详见链接六)
- 假设最开始的基准数据为数组第一个元素23,则首先用一个临时变量去存储基准数据,即tmp=23;然后分别从数组的两端扫描数组,设两个指示标志:low指向起始位置,high指向末尾.

- 首先从后半部分开始,如果扫描到的值大于基准数据就让high减1,如果发现有元素比该基准数据的值小(如上图中18<=tmp),就将high位置的值赋值给low位置 ,结果如下:

- 然后开始从前往后扫描,如果扫描到的值小于基准数据就让low加1,如果发现有元素大于基准数据的值(如上图46=>tmp),就再将low位置的值赋值给high位置的值,指针移动并且数据交换后的结果如下:
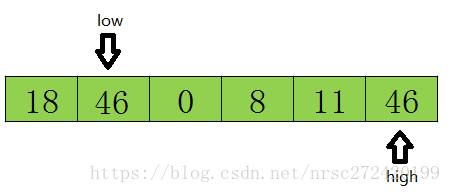
- 然后再开始从后向前扫描,原理同上,发现上图11<=tmp,则将low位置的值赋值给high位置的值,结果如下:

- 然后再开始从前往后遍历,直到low=high结束循环,此时low或high的下标就是基准数据23在该数组中的正确索引位置.如下图所示.

- 这样一遍走下来,可以很清楚的知道,其实快速排序的本质就是把基准数大的都放在基准数的右边,把比基准数小的放在基准数的左边,这样就找到了该数据在数组中的正确位置.
代码调试中的问题和解决过程
-
问题1:在递归二分查找中,如何使用Comparable,解释Comparable和Comparato
-
问题1解决方案:(详见链接二、四)
-
相同:
- Comparable和Comparator都是用来实现对象的比较、排序要想对象比较、排序,都需要实现Comparable或Comparator接口
- Comparable和Comparator都是Java的接口
-
不同:
- Comparator位于java.util包下,而Comparable位于java.lang包下
- Comparable接口的实现是在类的内部(如 String、Integer已经实现了Comparable接口,自己就可以完成比较大小操作),Comparator接口的实现是在类的外部(可以理解为一个是自已完成比较,一个是外部程序实现比较)
- 实现Comparable接口要重写compareTo方法,实现Comparator需要重写 compare 方法
-
总结:
- 如果比较的方法只要用在一个类中,用该类实现Comparable接口就可以
- 如果比较的方法在很多类中需要用到,就自己写个类实现Comparator接口,这样当要比较的时候把实现了Comparator接口的类传过去就可以,省得重复造轮子。这也是为什么Comparator会在java.util包下的原因。
- 使用Comparator的优点是:1.与实体类分离 2.方便应对多变的排序规则
-
递归二分查找
//二分查找,递归实现 recursion
public static int binarySearch_r(int[] a,int low,int high,int key) {
int mid = (low+high)/2;
if(low>=high)
return -1;
if(a[mid]==key)
return mid;
if(a[mid]>key)
return binarySearch_r(a,low,mid-1,key);
return binarySearch_r(a,mid+1,high,key);
}
- 问题2:书上线性查找方法不省时间,如何解决?
- 问题2解决方案:(详见PPT)
- 问题3:二叉树的性质与方法
- 问题3解决方案:(详见链接一)
- 在二叉树的第i层至多有2^(i-1)个结点(i≥1);
- 深度为k的二叉树至多有2^k-1个结点(k≥1);
- 对任意一棵二叉树,如果其终端结点数为n0,度为2 的结点数为n2,则,n0=n2+1
- 具有n个结点的完全二叉树的深度不大于log2 n的最大整数加1
- 包含n个结点的二叉树的高度至少为log2 (n+1)
- 如果对一棵有n个结点的完全二叉树的结点按层序编号(从第一层到最后一层,每层从左到右),则对任一结点(1≤i≤n)有:
- 如果i=1,则结点i是二叉树的根,无双亲;
- 如果i>1,则其双亲是结点x(其中结点x是 不大于i/2的最大整数)
- 如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i
- 如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1
- delect
总结删除结点的思路 delete方法
1、如果该结点同时存在左右子结点
获取后继结点;
转移后继结点值到当前结点node;
把要删除的当前结点设置为后继结点successor。
2、经过步骤1的处理,下面两种情况,只能是一个结点或者没有结点。
不管有没有结点,都获取子结点child
if child!=null,就说明有一个结点的情况,此时将父结点与子结点关联上
if 当前结点没有父结点(后继情况到这一定有父结点),说明要删除的就是根结点,
根结点设置为child
else if 当前结点是父结点的左结点
则将父结点的左结点设置为child
else 当前结点是父结点的右结点
则将父结点的右结点设置为child
3、返回被删除的结点node
总代码
代码托管第十三章
书本代码第十三章
(statistics.sh脚本的运行结果截图)

上周考试错题总结
最近无检测,故无错题
点评过的同学博客和代码
- 本周结对学习情况
- 20182326
- 结对照片


- 结对学习内容
- 学习查找
- 学习排序
- 上周博客互评情况
其他(感悟、思考等,可选)
太忙了,在夹缝中生存,忙里打代码,下周加油!
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 69/69 | 2/2 | 30/30 | Scanner |
| 第二、三周 | 529/598 | 3/5 | 25/55 | 部分常用类 |
| 第四周 | 300/1300 | 2/7 | 25/80 | junit测试和编写类 |
| 第五周 | 2665/3563 | 2/9 | 30/110 | 接口与远程 |
| 第六周 | 1108/4671 | 1/10 | 25/135 | 多态与异常 |
| 第七周 | 1946/6617 | 3/13 | 25/160 | 栈、队列 |
| 第八周 | 831/7448 | 1/14 | 25/185 | 查找、排序 |
尝试一下记录「计划学习时间」和「实际学习时间」,到期末看看能不能改进自己的计划能力。这个工作学习中很重要,也很有用。
耗时估计的公式:Y=X+X/N ,Y=X-X/N,训练次数多了,X、Y就接近了。
-
计划学习时间:30小时
-
实际学习时间:25小时
-
改进情况:
这周的别的事情较多,所以很急,以后一定好好把本次课程复习一下。