P4878 [USACO05DEC]layout布局（差分约束）

题意翻译

正如其他物种一样，奶牛们也喜欢在排队打饭时与它们的朋友挨在一起。FJ 有编号为 1…N1dots N1…N 的 NNN 头奶牛 (2≤N≤1000)(2le Nle 1000)(2≤N≤1000)。开始时，奶牛们按照编号顺序来排队。奶牛们很笨拙，因此可能有多头奶牛在同一位置上。

有些奶牛是好基友，它们希望彼此之间的距离小于等于某个数。有些奶牛是情敌，它们希望彼此之间的距离大于等于某个数。

给出 MLM_LML​ 对好基友的编号，以及它们希望彼此之间的距离小于等于多少；又给出 MDM_DMD​ 对情敌的编号，以及它们希望彼此之间的距离大于等于多少 (1≤ML,(1le M_L,(1≤ML​, MD≤104)M_Dle 10^4)MD​≤104)。

请计算：如果满足上述所有条件，111 号奶牛和 NNN 号奶牛之间的距离最大为多少。

输入输出格式

输入格式

第一行：三个整数 N,ML,MDN, M_L, M_DN,ML​,MD​，用空格分隔。

第 2…ML+12dots M_L+12…ML​+1 行：每行三个整数 A,B,DA, B, DA,B,D，用空格分隔，表示 AAA 号奶牛与 BBB 号奶牛之间的距离须 ≤Dle D≤D。保证 1≤A<B≤N,1le A<Ble N,1≤A<B≤N, 1≤D≤1061le Dle 10^61≤D≤106.

第 ML+2…ML+MD+1M_L+2dots M_L+M_D+1ML​+2…ML​+MD​+1 行：每行三个整数 A,B,DA, B, DA,B,D，用空格分隔，表示 AAA 号奶牛与 BBB 号奶牛之间的距离须 ≥Dge D≥D。保证 1≤A<B≤N,1le A<Ble N,1≤A<B≤N, 1≤D≤1061le Dle 10^61≤D≤106.

输出格式

一行，一个整数。如果没有合法方案，输出 -1. 如果有合法方案，但 111 号奶牛可以与 NNN 号奶牛相距无穷远，输出 -2. 否则，输出 111 号奶牛与 NNN 号奶牛间的最大距离。

题目背景

13组数据，前10组为原数据，后3组为hack数据

题目描述

Like everyone else, cows like to stand close to their friends when queuing for feed. FJ has N (2 <= N <= 1,000) cows numbered 1..N standing along a straight line waiting for feed. The cows are standing in the same order as they are numbered, and since they can be rather pushy, it is possible that two or more cows can line up at exactly the same location (that is, if we think of each cow as being located at some coordinate on a number line, then it is possible for two or more cows to share the same coordinate).

Some cows like each other and want to be within a certain distance of each other in line. Some really dislike each other and want to be separated by at least a certain distance. A list of ML (1 <= ML <= 10,000) constraints describes which cows like each other and the maximum distance by which they may be separated; a subsequent list of MD constraints (1 <= MD <= 10,000) tells which cows dislike each other and the minimum distance by which they must be separated.

Your job is to compute, if possible, the maximum possible distance between cow 1 and cow N that satisfies the distance constraints.

输入输出格式

输入格式：

Line 1: Three space-separated integers: N, ML, and MD.

Lines 2..ML+1: Each line contains three space-separated positive integers: A, B, and D, with 1 <= A < B <= N. Cows A and B must be at most D (1 <= D <= 1,000,000) apart.

Lines ML+2..ML+MD+1: Each line contains three space-separated positive integers: A, B, and D, with 1 <= A < B <= N. Cows A and B must be at least D (1 <= D <= 1,000,000) apart.

输出格式：

Line 1: A single integer. If no line-up is possible, output -1. If cows 1 and N can be arbitrarily far apart, output -2. Otherwise output the greatest possible distance between cows 1 and N.

输入输出样例

输入样例#1： 复制

4 2 1
1 3 10
2 4 20
2 3 3

输出样例#1： 复制

27

说明

Explanation of the sample:

There are 4 cows. Cows #1 and #3 must be no more than 10 units apart, cows #2 and #4 must be no more than 20 units apart, and cows #2 and #3 dislike each other and must be no fewer than 3 units apart.

The best layout, in terms of coordinates on a number line, is to put cow #1 at 0, cow #2 at 7, cow #3 at 10, and cow #4 at 27.

---

---

开始以为某两个奶牛的前后问题，发现想多了，编号大的奶牛位置一定比编号小的大，所以直接朴素的建边就行了

即

5 0 4

5 2 1

4 5 1

4 3 1

3 2 1

Ans = -1

如果按照题意，这数据并不存在，因为B>=A

如果从一开始的话就会被认为是-2，但其实是无解的（存在负环）

我们可以从每个点进行SPFA,找到负环，printf("-1");exit(0);

我们可以在建一个点，比如：0（任意一个不在图中的点），往每一个点建一条0的边，再从0 SPFA，这样就实现了每个点SPFA

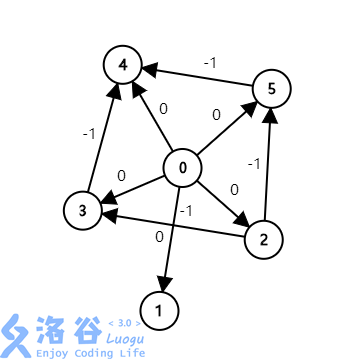
不连通就是没有约束调节，有无数个解

有负环就是无解

否则输出答案

---

---

// luogu-judger-enable-o2
#include"bits/stdc++.h"
using namespace std ;
typedef long long ll;

int n,ml,md;
const int nn = 1e6;
int link[nn],nxt[nn],son[nn],w[nn];
int tote;
int inc[2000];

inline void edge(int x,int y,int z)
{
  nxt[++tote]=link[x];
  link[x]=tote;
  son[tote]=y;
  w[tote]=z;

}

ll dis[2000];
int vis[2000];
inline void spfa(int s)
{
    queue<int >q;
    memset(vis,0,sizeof vis);
    q.push(s);
    dis[s]=0;
    while (!q.empty())
    {
       int t= q.front(); q.pop(); vis[t]=0;

       for (int i=link[t];i;i=nxt[i])
       {
         int so = son[i];
         if (dis[so]>dis[t]+w[i])
         {
            dis[so] = dis[t] + w[i];
            if (!vis[so])
            {
               q.push(so);
               vis[so]=1;
               if (++inc[so]>n)
               {
                  cout<<"-1";
                  exit(0);
               }
            }
         }

       }
    }



}



int main()
{
   cin>>n>>ml>>md;

   for (int i=1;i<=ml;i++)
   {
      int a,b,c;
      scanf("%d%d%d",&a,&b,&c);
      edge(a,b,c);
   }
   for (int i=1;i<=md;i++)
   {
      int a,b,c;
      scanf("%d%d%d",&a,&b,&c);
      edge(b,a,-c);
   }

   for (int i=1;i<=n;i++)
   {
      edge(0,i,0);
   }
    for (int i=1;i<=n;i++) dis[i]=1e18;
   spfa(0);
   //memset(dis,0x3f3f3f3f,sizeof dis);
   memset(inc,0,sizeof inc);
   for (int i=1;i<=n;i++) dis[i]=1e18;
   spfa(1);

   if(dis[n]==1e18) cout<<-2;
   else cout<<dis[n];



}