字符串编辑距离
是⼀种字符串之间相似度计算的⽅法。给定两个字符串S、T,将S转换成T所需要的删除,插
⼊,替换操作的数量就叫做S到T的编辑路径。⽽最短的编辑路径就叫做字符串S和T的编辑距
离。
举个例⼦:S=“eeba” T="abac" 我们可以按照这样的步骤转变:(1) 将S中的第⼀个e变成a;(2) 删
除S中的第⼆个e;(3)在S中最后添加⼀个c; 那么S到T的编辑路径就等于3。当然,这种变换并不是
唯⼀的,但如果3是所有变换中最⼩值的话。那么我们就可以说S和T的编辑距离等于3了。
动态规划解决编辑距离
动态规划(dynamic programming)是⼀种解决复杂问题最优解的策略。它的基本思路就是:将⼀
个复杂的最优解问题分解成⼀系列较为简单的最优解问题,再将较为简单的的最优解问题进⼀步
分解,直到可以⼀眼看出最优解为⽌。
动态规划算法是解决复杂问题最优解的重要算法。其算法的难度并不在于算法本身的递归难以实
现,⽽主要是编程者对问题本身的认识是否符合动态规划的思想。现在我们就来看看动态规划是
如何解决编辑距离的。

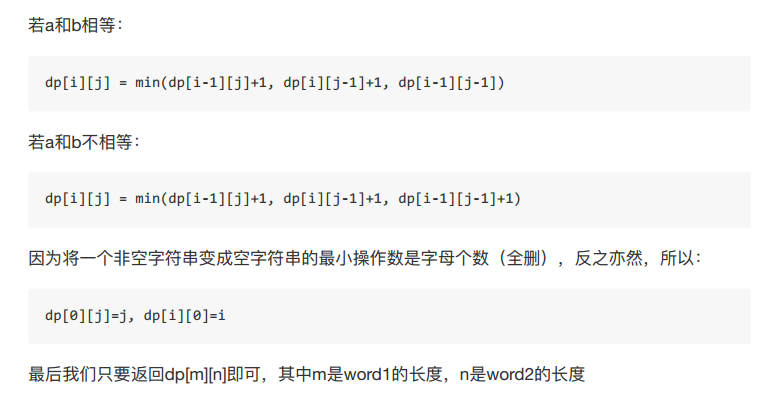
1 int minDistance(string word1,string word2){ 2 int m=word1.length(),n=word2.length(); 3 int[][] dp=new int[m+1][n+1]; 4 //初始化空字符串情况 5 for(int i=1;i<=m;i++){ 6 dp[i][0]=i; 7 } 8 for(int i=1;i<=n;i++){ 9 dp[0][i]=i; 10 } 11 for(int i=1;i<=m;i++){ 12 for(int j=1;j<=n;j++){ 13 //增加 14 int insertion =dp[i][j-1]+1; 15 //删除 16 int deletion =dp[i-1][j]+1; 17 //替换 18 int replae =dp[i-1][j-1]+(word1.charAt(i-1) ==word2.charAt(j-1)?0:1; 19 //三者得最小 20 dp[i][j]=min(replace,min(insertion,deletion); 21 } 22 } 23 retrurn dp[m][n]; 24 }