devinwang:检验你们学习成果。
我:我题解都看不懂。
-
首先,如果一共有 \(m\) 个 0,那么 \(ans \le \lfloor \frac m 2 \rfloor\)。
-
把左半边的 \(\lfloor \frac m 2 \rfloor\) 的 0 所划出的区间分成一组,右半边剩下的分成一组。分别称为 L 组、R 组。
实际上,一定存在一种最优方案满足所有最终取了的 \(b\) 的左 0 只在 L 集合中取,右 0 只在 R 集合中取。
因为对于一个 L 组的 \(b\),他的左 0 显然是得在 L 组中取了。对于右 0,即使所有的 \(b\) 的右 0 都在 R 组里取,那么也够了。
-
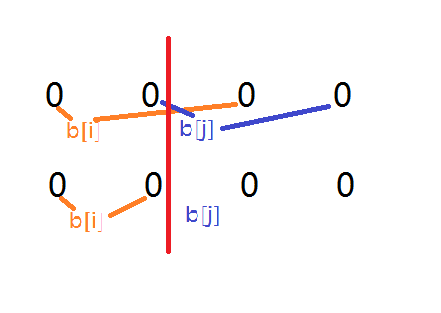
不妨将 \(b_i\) 相等的称为同种颜色,
对于一种最终选择取了的颜色 \(x\),
设 \(L_x\) 为 L 组中该颜色最靠右的那个
设 \(R_x\) 为 R 组中该颜色最靠左的那个
一定存在一种最优方案选取的那个 \(i\) 是 \(L_x/R_x\)
对于 \(L_x\) 他右侧肯定够,所以只考虑左0。
对于 \(R_x\) 他左侧肯定够,所以只考虑右0。
-
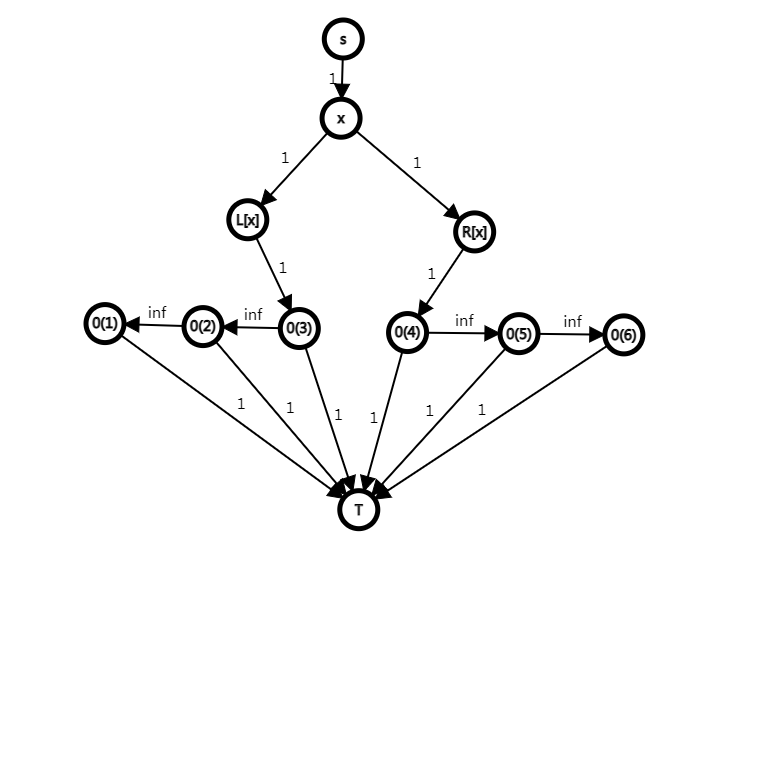
对于每种颜色,允许选一个。
对于每个 \(L_x\),考虑通过哪个右 0 过去。
对于每个 \(R_x\),考虑通过哪个左 0 过去。
每个 0 只能使用一次。
那么可以建出这样一张图,跑最大流。
-
数据范围是 \(10^5\),不能直接跑。模拟网络流。
因为最大流 = 最小割,我们只要计算出最小割就行了。
最小割一定是由一些前缀 0 到 T 的边 + 一些后缀 0 到 T 的边 + S 到 一些颜色的边组成的。
考虑枚举割断的前缀 0 到 T 的边的个数,然后要在 \(O(\log n)\) 的时间里计算出当前的最小割。
ans= 割断的 0 到 T 边数 + 总颜色数 - 割断的 0 到 T 的边已经覆盖的颜色数
也就是说只要维护当前 割掉的后缀 0 到 T 的边数 + 未被覆盖的颜色数 的最小值
用线段树维护,当颜色 \(x\) 的 \(L_x\) 被覆盖时,将割掉的后缀 0 个数 \(\in [R_x,cntr]\) 的答案减 1,割断的 0 到 T 的边已经覆盖了颜色 \(x\),不再需要割颜色边。
注意特判只在 L 组出现的颜色 和 只在 R 组出现的颜色。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mkp make_pair
#define pb push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define ls(x) ((x) << 1)
#define rs(x) ((x) << 1 | 1)
#define fi first
#define se second
const int N = 5e5 + 10, inf = 0x3f3f3f3f;
int n;
int lz[N << 2], tr[N << 2], num[N], pre[N], suf[N], lx[N], rx[N];
bool vis[N];
void pushdown(int rt) {
if(lz[rt]) {
lz[ls(rt)] += lz[rt]; tr[ls(rt)] += lz[rt];
lz[rs(rt)] += lz[rt]; tr[rs(rt)] += lz[rt];
lz[rt] = 0;
}
return;
}
void pushup(int rt) {
tr[rt] = min(tr[ls(rt)], tr[rs(rt)]);
}
void build(int rt, int l, int r) {
if(l == r) {
return tr[rt] = l, void();
}
pushdown(rt);
int mid = (l + r) / 2;
build(ls(rt), l, mid);
build(rs(rt), mid + 1, r);
pushup(rt);
}
void update(int rt, int l, int r, int L, int R) {
if(L <= l && r <= R) {
lz[rt]--; tr[rt]--;
return;
}
pushdown(rt);
int mid = (l + r) / 2;
if(L <= mid) update(ls(rt), l, mid, L, R);
if(R > mid) update(rs(rt), mid + 1, r, L, R);
pushup(rt);
}
void clear() {
for(int i = 1; i <= n; i++)
vis[i] = lx[i] = rx[i] = 0;
for(int i = 1; i <= (n << 2); i++)
lz[i] = 0, tr[i] = inf;
}
void solve() {
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d", &num[i]), vis[num[i]] = 1;
pre[0] = suf[n + 1] = 0;
for(int i = 1; i <= n; i++)
pre[i] = pre[i - 1] + !num[i];
for(int i = n; i >= 1; i--)
suf[i] = suf[i + 1] + !num[i];
int cntl = pre[n] / 2, cntr = pre[n] - cntl;
build(1, 0, cntr);
for(int i = 1; i <= n; i++) {
if(pre[i] > cntl) break;
lx[num[i]] = i;
}
for(int i = n; i >= 1; i--) {
rx[num[i]] = i;
if(suf[i] >= cntr) break;
}
int col = 0;
for(int i = 1; i <= n; i++)
if(vis[i]) col++;
int ans = min(pre[n] / 2, col);
for(int i = 1; i <= n; i++)
if(vis[i] && !lx[i]) {
update(1, 0, cntr, suf[rx[i]], cntr);
ans = min(ans, col + tr[1]);
}
for(int i = 1; i <= n; i++) {
if(pre[i] > cntl) break;
int u = num[i];
if(u && lx[u] == i) {
if(!rx[u]) update(1, 0, cntr, 0, cntr);
else update(1, 0, cntr, suf[rx[u]], cntr);
ans = min(ans, col + tr[1] + pre[i]);
}
}
printf("%d\n", ans);
clear();
return;
}
int main(){
memset(tr, 0x3f, sizeof(tr));
int T; scanf("%d", &T);
while(T--) solve();
return 0;
}
/*
8
1
1
2
0 0
3
0 1 0
6
0 0 1 2 0 0
6
0 1 0 0 1 0
6
0 1 3 2 0 0
6
0 0 0 0 5 0
12
0 1 0 2 2 2 0 0 3 3 4 0
*/