回滚莫队分块

回滚莫队分块

在莫队算法中，需要支持快速修改已知区间中单个元素、更新答案，以实现向答案区间转移。

然而，在某些问题中，修改后的更新会变得比较困难：比如删除之后，你更新答案为次大，过一会又需要删除，你又要把答案更新为次次大... 又或者修改之后要 (O(n)) 重新统计答案...等等。

假如你很勇的话，就可以开满空间来把所有 (k) 大存下来，或者直接暴力重新统计答案。不过这样看起来很鸡儿蠢（你都暴力了那还要莫队干什么），并且评测机也会毫不留情的甩给你一个 MLE 或者 TLE 。

这个时候，你需要让你的莫队“滚”起来。

Part 1 回滚莫队原理

回滚莫队是通过调整求解问题顺序从而避免低效的添加、删除操作的一种改进版莫队算法。它适用于普通莫队中添加或者删除操作之一难以有效进行的情况。具体来讲，回滚莫队分为两种：一种是“不删除莫队”，一种是“不添加莫队”。顾名思义，这两种回滚莫队分别避免了普通莫队中的一种操作。

不删除莫队

• 考虑用静态莫队求解一个区间问题。其中“添加”操作后更新答案方便，而“删除”操作则难以快速更新答案。

解决办法：

1. 类似普通莫队，先对原序列分块，然后把询问按照左端点所在块升序为第一关键字，右端点升序为第二关键字进行排序。记询问 (Q_i([l,r])) 属于元素 (A_l) 所在块。

2. 如果一个询问左右端点都在块 (T) 内的话，直接暴力求解。

3. 考虑对属于某一块 (T) 内的询问（左右端点属于不同块）集中求解。根据排序方式，这些询问的右端点 (r_i) 单调递增，左端点乱序。把已知区间 (l,r) 指针分别移动到块 (T+1) 的开头和块 (T) 的末尾，此时已知区间 ([l,r]) 为空区间。

4. 向右移动 (r) （添加元素）到询问的 (r_i) 位置，同时更新计数数组和答案（右端点升序，不用担心 (r) 可能向左挪的问题）。

5. 新建一个指针 (l_1) ，初始和 (l) 指针位置相同，记录此时的答案为 (tmp) 。向左移动 (l_1) （添加元素）到询问的 (l_i) 位置，同时更新计数数组和答案。这时得到这次询问的答案，记录下来。向右移动 (l_1) 指针（删除元素），让它回到 (l) 的位置，只更新计数数组，不更新答案。(l_1) 指针回到 (l) 的位置后，把答案赋值为 (tmp) 。

6. 当求解完一个区间的所有询问之后，清空计数数组，重复步骤 2、3 ，直到求解完成。

其中第 5 步就是所谓的“回滚”。其实质是移动 (l) 后再把它还原到移动之前的版本，这样既得到了答案，又可以保证不会出现“删除”操作。因为块 (T) 内的询问左端点必然在块 (T) 的结尾（ (l) 指针的位置）之前，每次从块 (T) 的末尾向左添加元素，必定可以达到询问左端点 (l_i) ，从而得到答案。

求解完一个区间的所有询问之后，要挪动 (l,r) 指针到下一个块继续求解。因为 ([l,r]) 一开始是空区间，计数数组里不可能有东西，所以要清空掉。

如果您还没有理解，请看图：

如图，绿色表示询问区间，其右端点单调递增。初始 (l,r) 指针在第 (T) 块（这里假定 (T=1) ）末尾的位置。

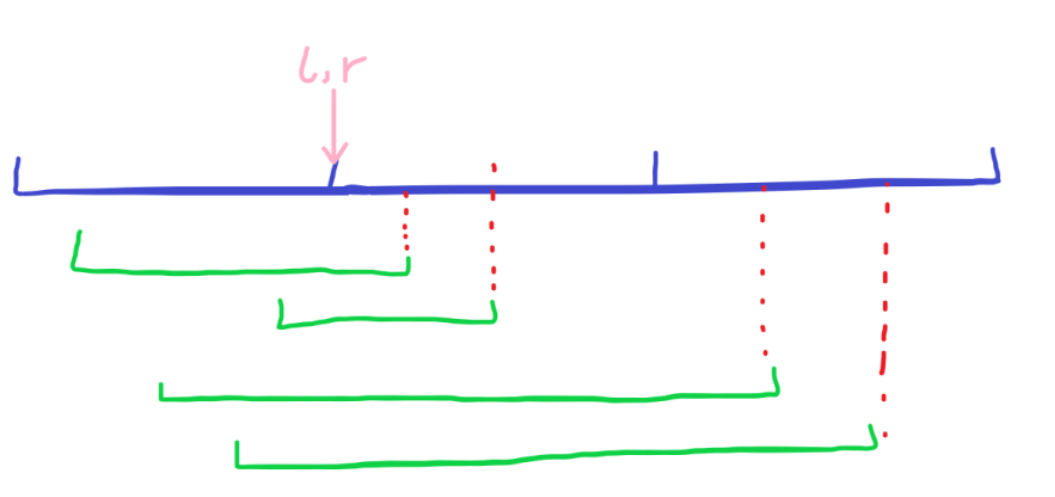
先移动 (r) 指针到第一个询问的右端点 (r_1) 的位置，更新计数数组和答案，此时橙色划出的区间答案已知，记为 (ans) 。

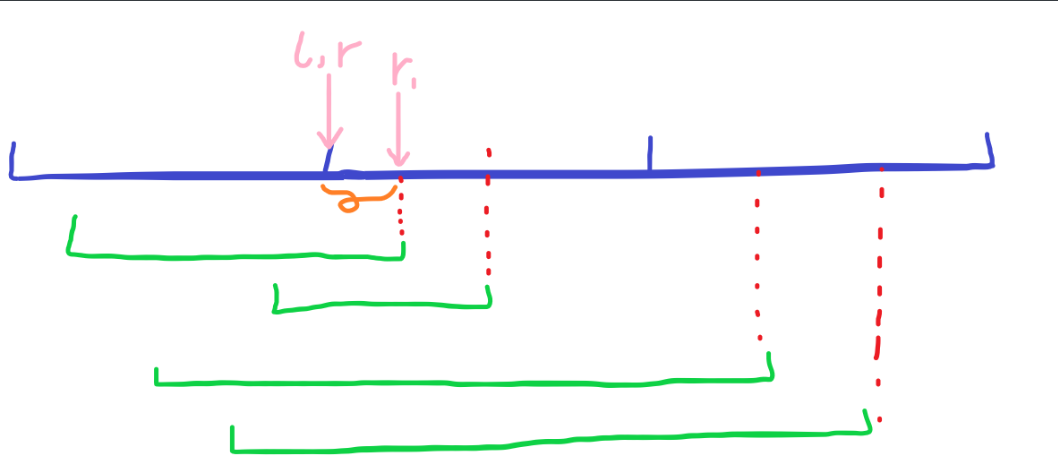
记录 (tmp=ans) ，复制左指针，准备向左移动并回滚。

把复制的指针移动到第一个询问的左端点 (l_1) 的位置，更新计数数组和答案。此时橙色画出的区间答案已知，即第一个询问的答案。

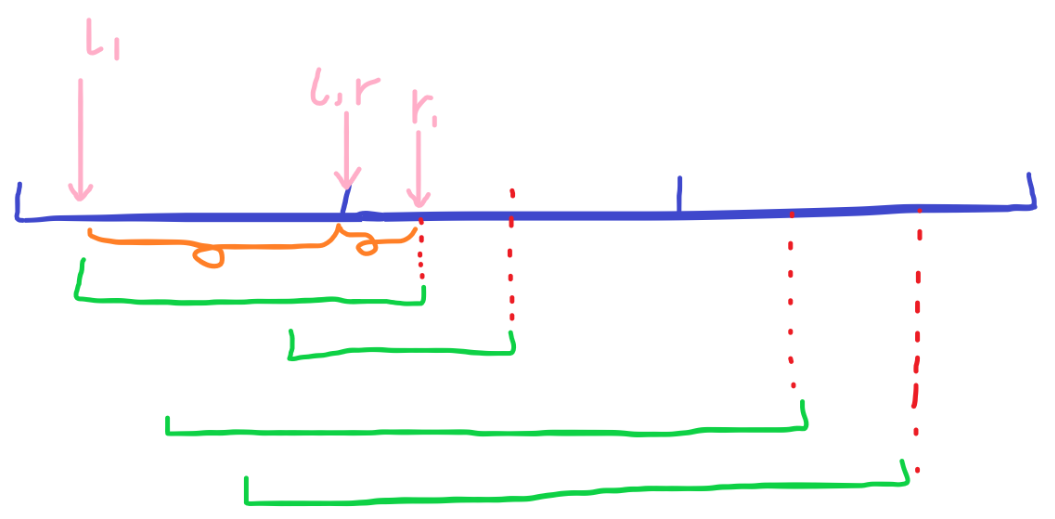
把复制的左指针挪回到 (l) 的位置，更新计数数组，但不更新答案。回到 (l) 之后把答案赋值为 (tmp) 。

这样相当于抛弃了一部分答案，把左指针回滚到块尾的位置重新统计（还原到移动左指针之前的版本）。

处理下一个询问，移动右指针到第二个询问的右端点 (r_2) ，更新计数数组和答案。橙色画出的区间答案已知。

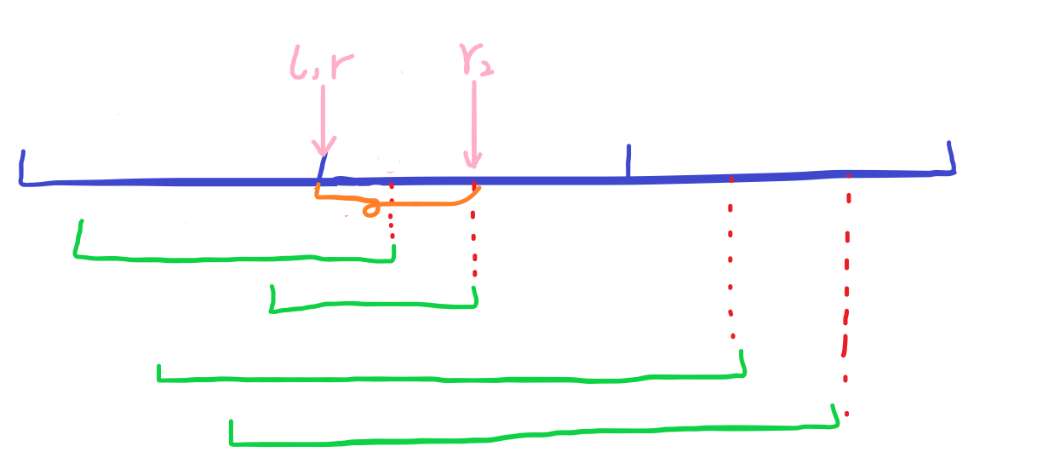
相似地，复制这个版本，移动左指针找到询问的答案，然后回滚还原到这个版本。

...... 之后的操作同上，不再赘述。

时间复杂度

• 对于左右端点在同一个块内地情况，暴力。复杂度不超过块长（(sqrt n)）；
• 同一块内，右端点单调递增，(r) 指针最多移动 (n) 次。一共 (sqrt n) 个块，总复杂度 (nsqrt n) ；
• 同一块内，左端点乱序，但相差不超过块长（(sqrt n)）。有 (m) 次询问，总复杂度 (msqrt n) ；

视 (m,n) 同数量级，不删除莫队总复杂度 (O(nsqrt n)) 。

不添加莫队

如果您已经完全理解了“不删除莫队”，那么“不添加莫队”就很简单了。

• 考虑用静态莫队求解一个区间问题。其中“删除”操作后更新答案方便，而“添加”操作则难以快速更新答案。

解决办法

使用“不添加莫队”之前，要确保整个序列可以正确的全部加入莫队中（把整个序列当作已知区间）。

1. 类似普通莫队，先对原序列分块，然后把询问按照左端点所在块升序为第一关键字，右端点降序为第二关键字进行排序。记询问 (Q_i([l,r])) 属于元素 (A_l) 所在块。

2. 如果一个询问左右端点都在块 (T) 内的话，直接暴力求解。

3. 考虑对属于某一块 (T) 内的询问（左右端点属于不同块）集中求解。根据排序方式，这些询问的右端点 (r_i) 单调递减，左端点乱序。把已知区间 (l,r) 指针分别移动到块 (T) 的开头和序列的末尾。

4. 向左移动 (r) （删除元素）到询问的 (r_i) 位置，同时更新计数数组和答案（右端点降序，不用担心 (r) 可能向左挪的问题）。

5. 新建一个指针 (l_1) ，初始和 (l) 指针位置相同，记录此时的答案为 (tmp) 。向右移动 (l_1) （删除元素）到询问的 (l_i) 位置，同时更新计数数组和答案。这时得到这次询问的答案，记录下来。向左移动 (l_1) 指针（添加元素），让它回到 (l) 的位置，只更新计数数组，不更新答案。(l_1) 指针回到 (l) 的位置后，把答案赋值为 (tmp) 。

6. 当求解完一个区间的所有询问之后，把计数数组更新到下一个状态。重复步骤 2、3 ，直到求解完成。

这里“把计数数组更新到下一个状态”的意思是求解完一个区间 (T) 之后，左指针从 (l_T) 变成了 (l_{T+1}) 。此时应该把已知区间由 ([l_T,n]) 调整为 ([l_{T+1},n]) ，这一步也可以通过“删除”操作实现。

因为块 (T) 内的询问左端点必然在块 (T) 的开头（ (l) 指针的位置）之后，每次从块 (T) 的开头向右删除元素，必定可以达到询问左端点 (l_i) ，从而得到答案。

如果您还没有理解，请看图：

如图，绿色表示询问区间，其右端点单调递减，橙色表示已知答案的区间。初始 (l) 指针在第 (T) 块（假定 (T=2) ）开头的位置，(r) 在序列末尾。

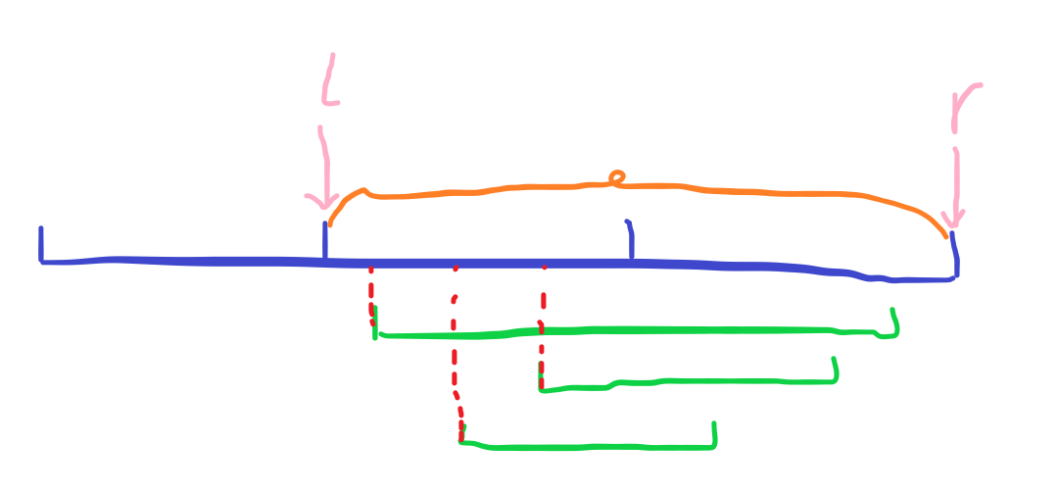
先移动 (r) 指针到第一个询问的右端点 (r_1) 的位置，更新计数数组和答案，记橙色划出的已知区间答案为 (ans) 。

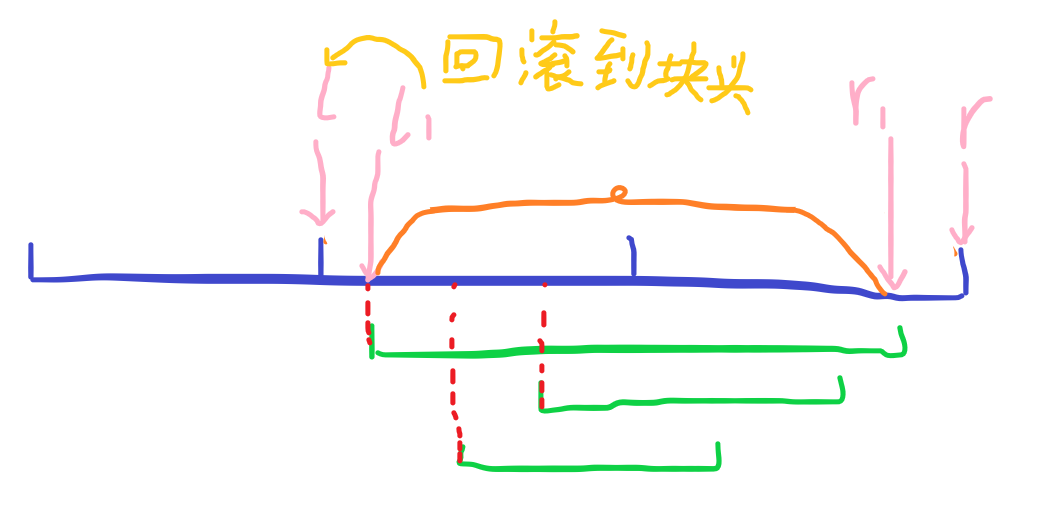
复制这个版本，移动左指针找到询问的答案（橙色部分），然后回滚还原到这个版本。

时间复杂度

证明方法同上，为 (O(nsqrt n)) 。

Part 2 回滚莫队例题

T1 【模板】回滚莫队&不删除莫队

这一道是不删除莫队的模板题。

题目链接：Link

题目描述：

给定一个长度为 (N) 的序列 (A) ，有 (m) 次询问，每次询问一个区间 ([l,r]) 内一对相同的数的最远间隔距离。

Solution：

这题删除操作不太好实现，如果恰好删掉了构成答案的一对数中的一个，无从得知下一个答案是多少。而添加操作可以用桶记录这个数出现的位置（一个最左边位置，一个最右边位置），边添加边更新答案（减一减）。考虑使用不删除莫队。

Code：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>

//using namespace std;

// #define int long long
const int maxn=200005;
#define ll long long

template <typename T>
inline T const& read(T &x){
  x=0;int fh=1;
  char ch=getchar();
  while(!isdigit(ch)){
	if(ch=='-')
	  fh=-1;
	  ch=getchar();
  }
  while(isdigit(ch)){
    x=(x<<3)+(x<<1)+ch-'0';
    ch=getchar();
  }
  x*=fh;
  return x;
}

int n,m,len,tot;
int A[maxn],B[maxn];
int bel[maxn],L[maxn],R[maxn];

struct Node{
  int l,r,org;
};

struct Node query[maxn];
inline bool operator < (const Node a,const Node b){
  return bel[a.l]!=bel[b.l]?bel[a.l]<bel[b.l]:a.r<b.r;
}//按上面提到的顺序排序

std::pair<int,int>cnt[maxn];//第一维记录这个数出现的最小下标，第二维记录出现的最大下标。
std::pair<int,int>cnt1[maxn];
//这个题比较特殊，因为cnt数组是直接赋值的，不能通过加减实现回滚，所以需要这个辅助数组。
int ans;

inline void addright(const int i){
  cnt[A[i]].first?cnt[A[i]].second=i:cnt[A[i]].first=cnt[A[i]].second=i;
  ans=std::max(ans,abs(cnt[A[i]].first-cnt[A[i]].second));
}
//在右端添加元素，更新的答案只可能来自添加位置减去最左端出现的位置

inline void addleft(const int i){
  cnt1[A[i]].second?cnt1[A[i]].first=i:cnt1[A[i]].first=cnt1[A[i]].second=i;
  ans=std::max(ans,cnt[A[i]].second?abs(cnt1[A[i]].first-cnt[A[i]].second):abs(cnt1[A[i]].first-cnt1[A[i]].second));
}
//在左端添加元素，利用辅助数组，避免破坏原来的cnt数组，方便回滚。

inline void del(const int i){
  cnt[A[i]].first=cnt[A[i]].second=0;
}//删除cnt数组中的元素（求解完整块询问后用来清空cnt数组用的）

inline void del1(const int i){
  cnt1[A[i]].first=cnt1[A[i]].second=0;
}//回滚辅助数组

inline void Init(){
  read(n);
  len=(int)std::sqrt(n);
  tot=n/len;
  for(int i=1;i<=tot;++i){
    if(i*len>n) break;
    L[i]=(i-1)*len+1;
    R[i]=i*len;//预处理每块的左右端点
  }
  if(R[tot]<n)
    tot++,L[tot]=R[tot-1]+1,R[tot]=n;
  for(int i=1;i<=n;++i){
    bel[i]=(i-1)/len+1;
    B[i]=read(A[i]);
  }
  std::sort(B+1,B+n+1);
  int l=std::unique(B+1,B+n+1)-B-1;
  for(int i=1;i<=n;++i)
    A[i]=std::lower_bound(B+1,B+l+1,A[i])-B;
  //原题数据范围较大，需要离散化
  read(m);
  for(int i=1;i<=m;++i)
    read(query[i].l),read(query[i].r),query[i].org=i;
}

int ans1[maxn];

signed main(){
  // freopen("P5906_1.in","r",stdin);
  // freopen("my.out","w",stdout);
  Init();
  std::sort(query+1,query+1+m);
  int l=R[bel[query[1].l]]+1,r=R[bel[query[1].l]],last=bel[query[1].l];//last表示当前在处理哪一块内的询问
  for(int i=1;i<=m;++i){
    if(bel[query[i].l]==bel[query[i].r]){//左右端点在同一块内，暴力求解
      for(int j=query[i].l;j<=query[i].r;++j)
        cnt1[A[j]].first?cnt1[A[j]].second=j:cnt1[A[j]].first=cnt1[A[j]].second=j;
      int tmp=0;
      for(int j=query[i].l;j<=query[i].r;++j)
        tmp=std::max(tmp,abs(cnt1[A[j]].first-cnt1[A[j]].second));
      for(int j=query[i].l;j<=query[i].r;++j)
        cnt1[A[j]].first=cnt1[A[j]].second=0;//别忘了暴力完也要还原
      ans1[query[i].org]=tmp;
      continue;
    }
    if(last^bel[query[i].l]){//要求解新一块内的询问了
      while(r>R[bel[query[i].l]])
        del(r--);
      while(l<R[bel[query[i].l]]+1)
        del(l++);//移动l，r指针到上面提到的位置，顺便清空cnt数组
      ans=0,last=bel[query[i].l];//清空答案重新统计
    }
    while(r<query[i].r)
      addright(++r);//右端点具有单调性，可以直接调整
    int tmp=ans,l1=l;
    while(l1>query[i].l)
      addleft(--l1);//调整左端点
    ans1[query[i].org]=ans;//记录答案
    while(l1<l)
      del1(l1++);//回滚，清空辅助数组
    ans=tmp;//还原之前的ans
  }
  for(int i=1;i<=m;++i)
    printf("%d
",ans1[i]);
  return 0;
}

T2 歴史の研究

日本题。

题目链接：Link

题目描述：

给定长度为 (N) 的序列 (A) ，有 (m) 次询问，每次询问区间 ([l,r]) 内最大的 (A_i imes T_{A_i}) 的值。

其中 (T_{A_i}) 表示 (A_i) 这个数在 ([l,r]) 内一共出现过的次数。

Solution：

显然，添加操作很好搞，直接维护一个桶和最大值，添加时取 max 就行了。删除操作不太好搞，如果删除了构成最大值的元素，无从得知下一个最大值源自哪里。考虑使用不删除莫队。

Code：

其他操作都差不多，代码不再详细注释。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>

//using namespace std;

// #define int long long
const int maxn=100005;
#define ll long long

template <typename T>
inline T const& read(T &x){
  x=0;int fh=1;
  char ch=getchar();
  while(!isdigit(ch)){
	if(ch=='-')
	  fh=-1;
	  ch=getchar();
  }
  while(isdigit(ch)){
    x=(x<<3)+(x<<1)+ch-'0';
	ch=getchar();
  }
  x*=fh;
  return x;
}

int n,m,len,tot;
int A[maxn],B[maxn];
int bel[maxn],L[maxn],R[maxn];

struct Node{
  int l,r,org;
};

struct Node query[maxn];
inline bool operator < (const Node a,const Node b){
  return bel[a.l]^bel[b.l]?bel[a.l]<bel[b.l]:a.r<b.r;
}

ll ans;
int cnt[maxn],cnt1[maxn];

inline void add(const int i){
  cnt[A[i]]++;
  ans=std::max(ans,1LL*cnt[A[i]]*B[A[i]]);
}

inline void del(const int i){
  cnt[A[i]]--;
}

inline void Init(){
  read(n),read(m);
  len=(int)std::sqrt(n);
  tot=n/len;
  for(int i=1;i<=tot;++i){
    if(i*len>n)
      break;
    L[i]=(i-1)*len+1;
    R[i]=i*len;
    //L[i],R[i] 表示第 i 块的左右端点
  }
  if(R[tot]<n)
    tot++,L[tot]=R[tot-1]+1,R[tot]=n;
  for(int i=1;i<=n;++i){
    bel[i]=(i-1)/len+1;
    B[i]=read(A[i]);
  }
    
  std::sort(B+1,B+n+1);
  int l=std::unique(B+1,B+n+1)-B-1;
  for(int i=1;i<=n;++i)
    A[i]=std::lower_bound(B+1,B+l+1,A[i])-B;
  // A[i]为离散化值
  // B[A[i]]为原值
  for(int i=1;i<=m;++i)
    read(query[i].l),read(query[i].r),query[i].org=i;
}

ll ans1[maxn];

signed main(){
  Init();
  std::sort(query+1,query+m+1);
  int l=R[bel[query[1].l]]+1,r=R[bel[query[1].l]],last=bel[query[1].l];
  for(int i=1;i<=m;++i){
    // 处理同一块中的询问
    if(bel[query[i].l]==bel[query[i].r]){
      for(int j=query[i].l;j<=query[i].r;++j)
        cnt1[A[j]]++;
      ll tmp=0;
      for(int j=query[i].l;j<=query[i].r;++j)
        tmp=std::max(tmp,1LL*cnt1[A[j]]*B[A[j]]);
      for(int j=query[i].l;j<=query[i].r;++j)
        cnt1[A[j]]--;
      ans1[query[i].org]=tmp;
      continue;
    }
    if(last^bel[query[i].l]){
      while(r>R[bel[query[i].l]])
        del(r--);
      while(l<R[bel[query[i].l]]+1)
        del(l++);
      ans=0,last=bel[query[i].l];
    }
    //直接移动右端点
    while(r<query[i].r)
      add(++r);
    //移动左端点回答问题
    int l1=l;
    ll tmp=ans;
    while(l1>query[i].l)
      add(--l1);
    ans1[query[i].org]=ans;
    //回滚还原
    while(l1<l)
      del(l1++);
    ans=tmp;
  }
  for(int i=1;i<=m;++i)
    printf("%lld
",ans1[i]);
  return 0;
}

T3 Rmq Problem / mex

题目链接：Link

题目描述：

给定一个长度为 (N) 的序列 (A) ，有 (m) 次询问，每次询问区间 ([l,r]) 内没有出现过的最小的自然数。

Solution：

用桶维护出现过的数字，那么答案就是第一个不在桶中出现的数字。

发现删除操作比较好实现，只要在删除的同时和答案比较看看是不是构成新的最小值即可。添加操作比较操蛋，如果把原来答案的位置塞进了一个数，我们不知道新的答案是多少。考虑使用不添加莫队。

Code：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>

//using namespace std;

// #define int long long
const int maxn=200005;
#define ll long long

template <typename T>
inline T const& read(T &x){
  x=0;int fh=1;
  char ch=getchar();
  while(!isdigit(ch)){
	if(ch=='-')
	  fh=-1;
	  ch=getchar();
  }
  while(isdigit(ch)){
    x=(x<<3)+(x<<1)+ch-'0';
	ch=getchar();
  }
  x*=fh;
  return x;
}

int n,m,len,tot;
int A[maxn];
int bel[maxn],L[maxn],R[maxn];

struct Node{
  int l,r,org;
};

struct Node query[maxn];
inline bool operator < (const Node a,const Node b){
  return bel[a.l]!=bel[b.l]?bel[a.l]<bel[b.l]:a.r>b.r;
}//按照上面提到的顺序排序

int cnt[maxn],cnt1[maxn],ans;

inline void add(const int i){
  cnt[A[i]]++;
}//添加时不用更新（回滚）

inline void del(const int i){
  cnt[A[i]]--;
  if(!cnt[A[i]])
    ans=std::min(ans,A[i]);
}//删除同时更新

int ans1[maxn];

void Init(){
  read(n),read(m);
  len=(int)std::sqrt(n);
  tot=n/len;
  for(int i=1;i<=tot;++i){
    if(i*len>n) break;
    L[i]=(i-1)*len+1;
    R[i]=i*len;
  }
  if(R[tot]<n)
    tot++,L[tot]=R[tot-1]+1,R[tot]=n;//同上预处理块的信息
  for(int i=1;i<=n;++i){
    bel[i]=(i-1)/len+1;
    read(A[i]);
  }
  
  for(int i=1;i<=n;++i)
    cnt[A[i]]++;
  while(cnt[ans])
    ans++;//先把整个序列当成已知序列，然后删除元素
  for(int i=1;i<=m;++i)
    read(query[i].l),read(query[i].r),query[i].org=i;
}

signed main(){
  Init();
  std::sort(query+1,query+1+m);
  int l=1,r=n,last=0;
  for(int i=1;i<=m;++i){
    if(bel[query[i].l]==bel[query[i].r]){//左右端点同段，直接暴力
      for(int j=query[i].l;j<=query[i].r;++j)
        cnt1[A[j]]++;
      int tmp=0;
      while(cnt1[tmp])
        tmp++;
      for(int j=query[i].l;j<=query[i].r;++j)
        cnt1[A[j]]--;
      ans1[query[i].org]=tmp;
      continue;
    }
    if(bel[query[i].l]!=last){//要处理新一块的询问
      while(r<n)
        add(++r);//回复r到序列末尾
      while(l<L[bel[query[i].l]])
        del(l++);
      int tmp=0;
      while(cnt[tmp])//统计[l_{T+1},n]的答案，以此为基础求解该块内的询问
        tmp++;
      ans=tmp;
      last=bel[query[i].l];
    }
    while(r>query[i].r)
      del(r--);//右端点单调，直接移动
    int tmp=ans,l1=l;
    while(l1<query[i].l)
      del(l1++);//移动左端点
    ans1[query[i].org]=ans;//得到询问的解
    while(l1>l)//回滚还原
      add(--l1);
    ans=tmp;
  }
  for(int i=1;i<=m;++i)
    printf("%d
",ans1[i]);
  return 0;
}