[USACO09JAN]安全出行Safe Travel（最短路径树）

传送门

求对于每个点删掉1到他的最短路上的最后一条边（就是这条路径上与他自己相连的那条边）后1到他的最短路的长度。

即：最短路径树：图中的源点到所有结点的最短路径构成的树。

最短路径树在dijkstra过程中就可以求出来，因为这个过程就相当于走一棵树。

然后就是选入杂边，对于一条杂边<u，v>，它加入后会形成一个环，这个环上所有的点除了lca都可以被这条杂边更新，即这些点删去它上面那条边后是可以走杂边的，但lca删去上面那条边后图就不连通了。

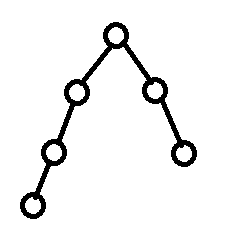
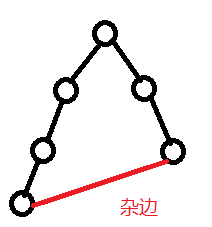
那么

disnew[x]=dis[u]+dis[v]+w[i]−dis[x]

对于一条杂边，前面那三个量是一定的。 每一个点，我们希望用最小的杂边更新他，更新过后就不再更新。 于是可以按w排序杂边，依次更新，更新过后的点就用并查集缩起来，以保证每个点只被更新一次。

//要题目中说了源点到每个点最短路径是唯一的 那往往都和最短路树有关系
#include<bits/stdc++.h>
#define N 100003
#define M 200003
#define INF 2100000000
using namespace std;
int read()
{
    int x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
int tot=1,n;
int head[N],dis[N],ans[N],dep[N],fa[N],pre[N],anc[N],ontree[M*2];
struct EDGE{
    int nextt,to,val;
}w[M*2];
struct Edge{
    int u,v,val;
}za[M*2];
struct qnode{
    int v,c;
    qnode(int _v=0,int _c=0):v(_v),c(_c){} 
    bool operator <(const qnode &r)const
    {
        return r.c<c;
    }
};
bool cmp(const Edge &a,const Edge &b)
{
    return a.val<b.val;
}
void add(int a,int b,int c)
{
    tot++;
    w[tot].nextt=head[a];
    w[tot].to=b;
    w[tot].val=c;
    head[a]=tot;
}
int get(int x)
{
    if(fa[x]==x)return x;
    return fa[x]=get(fa[x]);
}
void dij()
{
    priority_queue<qnode>q;
    for(int i=1;i<=n;++i)dis[i]=INF;
    dis[1]=0;
    q.push(qnode(1,0));
    while(!q.empty())
    {
        qnode e=q.top();q.pop();
        int u=e.v;
        for(int i=head[u];i;i=w[i].nextt)
        {
            int v=w[i].to;
            if(dis[v]>dis[u]+w[i].val)
            {
                dis[v]=dis[u]+w[i].val;
                pre[v]=i;anc[v]=u;dep[v]=dep[u]+1;
                q.push(qnode(v,dis[v]));
            }
        }
    }
}
int main()
{
      n=read();int m=read();
      for(int i=1;i<=m;++i)
      {
          int a=read(),b=read(),c=read();
          add(a,b,c);add(b,a,c);
    }
    dij();
    
    for(int i=2;i<=n;++i)ontree[pre[i]]=1;
    for(int i=1;i<=n;++i)fa[i]=i,ans[i]=INF;
    int cnt=0;
    for(int i=2;i<=tot;++i)
      if(!ontree[i]&&!ontree[i^1])
      {
          za[++cnt].u=w[i].to;
          za[cnt].v=w[i^1].to;
          za[cnt].val=dis[w[i].to]+dis[w[i^1].to]+w[i].val;
      }
    sort(za+1,za+1+cnt,cmp);
    for(int i=1;i<=cnt;++i)
    {
        int u=za[i].u,v=za[i].v;
        u=get(u);v=get(v);
        while(u!=v)
        {
            if(dep[u]<dep[v])swap(u,v);//从下往上并上去 
            ans[u]=min(ans[u],za[i].val-dis[u]);
            u=fa[u]=get(anc[u]);
        }
    }
    for(int i=2;i<=n;++i)
    {
        if(ans[i]<INF)printf("%d
",ans[i]);
        else printf("-1
");
    }
}