题目描述
平面上有(n)条线段,你要擦掉所有线段但保留原有的(2n)个端点,然后连接这些端点形成(n)条不相交的线段,每个端点只能在一条线段中。
假设你画的线段总长为(Y),原有线段的总长为(X),你要满足(Ygeq frac{2}{pi}X)
(nleq 5000)
题解
我们先随便画一个向量,把所有向量投影到这个向量上面。
若一个确定的向量(overrightarrow a)的倾角为(x),另一个随机的单位向量(overrightarrow b)的倾角为( heta),那么(overrightarrow a)在(overrightarrow b)上的投影的长度为(|a||cos (x- heta)|)。这个东西的期望为(|a|frac{2}{pi})。
所以随机一个向量,所有向量在这个向量的投影上的长度之和(>frac{2}{pi}X)的概率为(frac{1}{2})。
你可以多随机几次,也可以用一个确定性的算法算出上面这个东西。
怎么算?
假设后面那部分没有绝对值符号。把(|a|cos(x- heta))展开成$|a|sin xsin heta+|a|cos xcos heta (,把这些东西加起来得到)csin heta + dcos heta(。现在我们要求这个东西的最大值。)(csin heta + dcos heta)'=ccos heta - d sin heta(,那么)frac{c}{d}= an heta$,然后就可以算出投影的长度。
但是现在有绝对值符号。
先把所有向量翻到(x)轴上方,按极角排序。
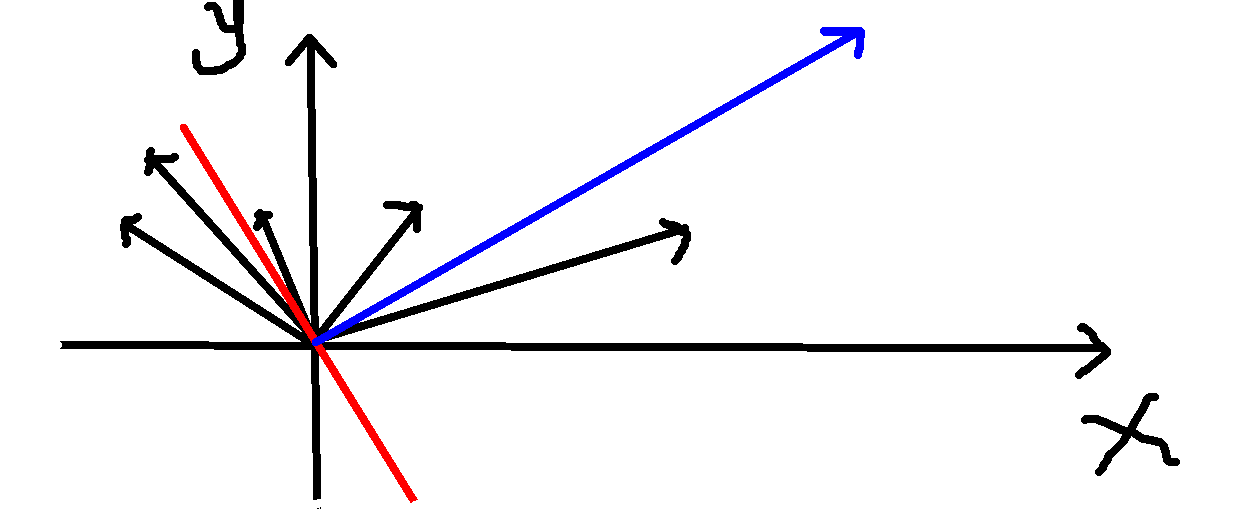
假设最优的是蓝色这个向量。
我们枚举和这个向量垂直的直线(红色),那么直线左边的向量(cos(x- heta))的符号就是负的,右边的就是正的。
所以我们可以在(O(nlog n))内把最优的向量算出来。
接下来把所有(2n)点投影在这个向量上,取左边一半的点作为我们要连的线段的左端点,右边一半的点作为右端点。这样连出来的长度肯定比原有的线段在这个向量上投影的长度大。
这样我们就得到了两个分离的点集,现在要在这两个点集间连线。
有两种方法:
第一种:取左下方的点集最左下的点,然后枚举右侧点集中的一个点,要求这两个点连成的直线下方的点中每个点集的点各占一半。把这两个点连起来,然后分治成小问题。
时间复杂度:期望(O(nlog^2n)),最坏(O(n^2log n))
第二种:求这两个点集合并后的凸包,删掉凸包上相邻两个属于不同的点集的点,把这两个点连起来,重复前面的过程。
时间复杂度:(O(n^2))
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<utility>
#include<vector>
using namespace std;
typedef pair<int,int> pii;
typedef pair<double,double> pdd;
typedef long long ll;
const double pi=acos(-1);
const double eps=1e-9;
struct point
{
double x,y;
point(){}
point(const double &a,const double &b):x(a),y(b){}
};
point operator +(point a,point b){return point(a.x+b.x,a.y+b.y);}
point operator -(point a,point b){return point(a.x-b.x,a.y-b.y);}
point operator *(point a,double b){return point(a.x*b,a.y*b);}
int operator <(point a,point b){if(a.x!=b.x)return a.x<b.x;return a.y<b.y;}
double dot(point a,point b){return a.x*b.x+a.y*b.y;}
double cross(point a,point b){return a.x*b.y-a.y*b.x;}
double len(point a){return sqrt(a.x*a.x+a.y*a.y);}
struct point2
{
int x,y;
point2(int a=0,int b=0)
{
x=a;
y=b;
}
};
point2 operator +(const point2 &a,const point2 &b){return point2(a.x+b.x,a.y+b.y);}
point2 operator -(const point2 &a,const point2 &b){return point2(a.x-b.x,a.y-b.y);}
point2 operator *(const point2 &a,const int &b){return point2(a.x*b,a.y*b);}
int operator <(const point2 &a,const point2 &b){if(a.x!=b.x)return a.x<b.x;return a.y<b.y;}
ll dot(const point2 &a,const point2 b){return (ll)a.x*b.x+(ll)a.y*b.y;}
ll cross(const point2 &a,const point2 &b){return (ll)a.x*b.y-(ll)a.y*b.x;}
double len(point2 a){return sqrt((double)a.x*a.x+(double)a.y*a.y);}
struct ppp
{
point2 x;
int y;
double v;
pdd a;
};
ppp c[10010];
point2 a[10010];
pii d[5010];
int cmp(ppp a,ppp b)
{
return a.v<b.v;
}
int n;
int link[10010];
int v1[10010],v2[10010];
int t1,t2;
int cmp2(int x,int y)
{
if(a[x].x!=a[y].x)
return a[x].x<a[y].x;;
return a[x].y<a[y].y;
}
int color[10010];
int b[10010];
int st[10010];
int top;
pdd operator +(pdd a,pdd b){return pdd(a.first+b.first,a.second+b.second);}
pdd operator -(pdd a,pdd b){return pdd(a.first-b.first,a.second-b.second);}
pdd f1[10010];
pdd f2[10010];
struct pppp
{
point x;
int y;
};
pppp e[10010];
int cmp3(pppp a,pppp b)
{
return a.x<b.x;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
#endif
scanf("%d",&n);
for(int i=1;i<=2*n;i++)
scanf("%d%d",&a[i].x,&a[i].y);
int x,y;
double s=0,ans;
for(int i=1;i<=n;i++)
{
scanf("%d%d",&d[i].first,&d[i].second);
s+=len(a[d[i].first]-a[d[i].second]);
c[i].x=a[d[i].second]-a[d[i].first];
if(c[i].x.y<0)
{
c[i].x.x=-c[i].x.x;
c[i].x.y=-c[i].x.y;
}
c[i].y=i;
c[i].v=atan2(c[i].x.y,c[i].x.x);
c[i].a.first=len(c[i].x)*sin(c[i].v);
c[i].a.second=len(c[i].x)*cos(c[i].v);
}
sort(c+1,c+n+1,cmp);
for(int i=1;i<=n;i++)
f1[i]=f1[i-1]+c[i].a;
double mx=0,angle;
for(int i=0;i<=n;i++)
{
double now_angle=atan2(f1[n].first-2*f1[i].first,f1[n].second-2*f1[i].second);
if(now_angle<0)
now_angle+=2*pi;
double now=(f1[n].first-2*f1[i].first)*sin(now_angle)+(f1[n].second-2*f1[i].second)*cos(now_angle);
if(now>mx)
{
mx=now;
angle=now_angle;
}
}
point r(cos(angle),sin(angle));
for(int i=1;i<=2*n;i++)
{
e[i].x=r*dot(point(a[i].x,a[i].y),r);
e[i].y=i;
}
sort(e+1,e+2*n+1,cmp3);
for(int i=1;i<=n;i++)
color[e[i].y]=1;
for(int i=n+1;i<=2*n;i++)
color[e[i].y]=2;
t1=t2=0;
for(int i=1;i<=2*n;i++)
v1[++t1]=i;
sort(v1+1,v1+t1+1,cmp2);
for(int i=1;i<=n;i++)
{
top=0;
t2=t1;
for(int i=1;i<=t1;i++)
v2[i]=v1[i];
for(int j=1;j<=t1;j++)
{
x=v1[j];
while(top>=2&&cross(a[x]-a[st[top-1]],a[st[top]]-a[st[top-1]])>0)
top--;
st[++top]=x;
}
int flag=1;
for(int i=1;i<top;i++)
if(color[st[i]]!=color[st[i+1]])
{
link[st[i]]=st[i+1];
link[st[i+1]]=st[i];
b[st[i]]=b[st[i+1]]=1;
flag=0;
i++;
}
if(flag)
{
top=0;
for(int j=t1;j>=1;j--)
{
x=v1[j];
while(top>=2&&cross(a[x]-a[st[top-1]],a[st[top]]-a[st[top-1]])>0)
top--;
st[++top]=x;
}
for(int i=1;i<top;i++)
if(color[st[i]]!=color[st[i+1]])
{
link[st[i]]=st[i+1];
link[st[i+1]]=st[i];
b[st[i]]=b[st[i+1]]=1;
i++;
}
}
t1=0;
for(int i=1;i<=t2;i++)
if(!b[v2[i]])
v1[++t1]=v2[i];
}
for(int i=1;i<2*n;i++)
if(link[i]>i)
printf("%d %d
",i,link[i]);
return 0;
}