题目描述
有一个((n+1) imes (m+1))的网格,每条边都有一个边权。有一些格子是城市。你要用一个环圈住所有城市,要求环上所有边的边权和最小。重合的边边权算多次。保证左上角((1,1))一定有一个城市。
(n,mleq 400)
题解
观察到左上角一定有一个城市。
首先求出每个城市左上角到((0,0))的最短路,那么这个圈肯定不会经过最短路。如果经过,那么把其中一部分换成最短路上的边不会更劣。
这样每个城市左上角到((0,0))的边都不能被穿过。另外,每个城市周围四条边都不能经过。
然后把每个点拆成四个点,每条边拆成四条边。如果有一条边不能穿过,那么就把这条边对应的边删掉。
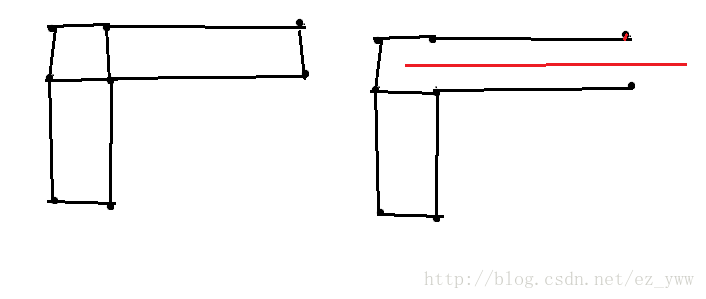
最后跑一个从((0,0))右上到((0,0))左下的最短路。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<ctime>
#include<utility>
#include<cmath>
#include<functional>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
void sort(int &a,int &b)
{
if(a>b)
swap(a,b);
}
void open(const char *s)
{
#ifndef ONLINE_JUDGE
char str[100];
sprintf(str,"%s.in",s);
freopen(str,"r",stdin);
sprintf(str,"%s.out",s);
freopen(str,"w",stdout);
#endif
}
int rd()
{
int s=0,c;
while((c=getchar())<'0'||c>'9');
do
{
s=s*10+c-'0';
}
while((c=getchar())>='0'&&c<='9');
return s;
}
void put(int x)
{
if(!x)
{
putchar('0');
return;
}
static int c[20];
int t=0;
while(x)
{
c[++t]=x%10;
x/=10;
}
while(t)
putchar(c[t--]+'0');
}
int upmin(int &a,int b)
{
if(b<a)
{
a=b;
return 1;
}
return 0;
}
int upmax(int &a,int b)
{
if(b>a)
{
a=b;
return 1;
}
return 0;
}
struct graph
{
int v[10000010];
int w[10000010];
int t[10000010];
int h[1000010];
int n;
void init()
{
n=0;
memset(h,0,sizeof h);
}
void add(int x,int y,int z)
{
n++;
v[n]=y;
w[n]=z;
t[n]=h[x];
h[x]=n;
}
};
graph g;
void add(int x,int y,int z)
{
g.add(x,y,z);
}
ll d[1000010];
int c[1000010];
int b[1000010];
queue<int> q;
void spfa(int S)
{
memset(d,0x7f,sizeof d);
c[S]=0;
d[S]=0;
q.push(S);
while(!q.empty())
{
int x=q.front();
q.pop();
b[x]=0;
for(int i=g.h[x];i;i=g.t[i])
if(d[g.v[i]]>d[x]+g.w[i])
{
d[g.v[i]]=d[x]+g.w[i];
c[g.v[i]]=x;
if(!b[g.v[i]])
{
q.push(g.v[i]);
b[g.v[i]]=1;
}
}
}
}
int a1[410][410];
int a2[410][410];
int a[410][410];
int n,m;
int id(int x,int y)
{
return x*(m+1)+y+1;
}
pii e[1000010];
int ban[410][410];
int ban2[410][410][5];
void gao2(int x1,int y1,int x2,int y2)
{
if(x1>x2)
{
swap(x1,x2);
swap(y1,y2);
}
if(y1>y2)
{
swap(x1,x2);
swap(y1,y2);
}
// fprintf(stderr,"%d %d %d %d
",x1,y1,x2,y2);
if(x2==x1+1)
ban2[x1][y1][3]=ban2[x2][y2][1]=1;
else
ban2[x1][y1][4]=ban2[x2][y2][2]=1;
}
void gao(int x,int y,int xx,int yy)
{
gao2(x,y,xx,yy);
if(ban[x][y])
return;
ban[x][y]=1;
if(x==0&&y==0)
return;
gao(e[c[id(x,y)]].first,e[c[id(x,y)]].second,x,y);
}
int main()
{
open("b");
scanf("%d%d",&n,&m);
int i,j;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
scanf("%d",&a[i][j]);
for(i=1;i<=n;i++)
for(j=0;j<=m;j++)
scanf("%d",&a1[i][j]);
for(i=0;i<=n;i++)
for(j=1;j<=m;j++)
scanf("%d",&a2[i][j]);
for(i=0;i<=n;i++)
for(j=0;j<=m;j++)
{
if(i<n)
add(id(i,j),id(i+1,j),a1[i+1][j]);
if(i)
add(id(i,j),id(i-1,j),a1[i][j]);
if(j<m)
add(id(i,j),id(i,j+1),a2[i][j+1]);
if(j)
add(id(i,j),id(i,j-1),a2[i][j]);
}
for(i=0;i<=n;i++)
for(j=0;j<=m;j++)
e[id(i,j)]=pii(i,j);
spfa(1);
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
if(a[i][j])
{
if(i!=1||j!=1)
gao(e[c[id(i-1,j-1)]].first,e[c[id(i-1,j-1)]].second,i-1,j-1);
gao2(i-1,j-1,i-1,j);
gao2(i-1,j,i,j);
gao2(i-1,j-1,i,j-1);
gao2(i,j-1,i,j);
}
ban2[0][0][1]=ban2[0][0][2]=1;
g.init();
for(i=0;i<=n;i++)
for(j=0;j<=m;j++)
{
if(i<n)
{
add(id(i,j)*4,id(i+1,j)*4-3,a1[i+1][j]);
add(id(i,j)*4-1,id(i+1,j)*4-2,a1[i+1][j]);
}
if(i)
{
add(id(i,j)*4-3,id(i-1,j)*4,a1[i][j]);
add(id(i,j)*4-2,id(i-1,j)*4-1,a1[i][j]);
}
if(j<m)
{
add(id(i,j)*4-2,id(i,j+1)*4-3,a2[i][j+1]);
add(id(i,j)*4-1,id(i,j+1)*4,a2[i][j+1]);
}
if(j)
{
add(id(i,j)*4-3,id(i,j-1)*4-2,a2[i][j]);
add(id(i,j)*4,id(i,j-1)*4-1,a2[i][j]);
}
if(!ban2[i][j][1])
{
add(id(i,j)*4-3,id(i,j)*4-2,0);
add(id(i,j)*4-2,id(i,j)*4-3,0);
}
if(!ban2[i][j][2])
{
add(id(i,j)*4-3,id(i,j)*4,0);
add(id(i,j)*4,id(i,j)*4-3,0);
}
if(!ban2[i][j][3])
{
add(id(i,j)*4,id(i,j)*4-1,0);
add(id(i,j)*4-1,id(i,j)*4,0);
}
if(!ban2[i][j][4])
{
add(id(i,j)*4-2,id(i,j)*4-1,0);
add(id(i,j)*4-1,id(i,j)*4-2,0);
}
}
spfa(2);
printf("%lld
",d[4]);
return 0;
}