1.本周学习总结(
1.思维导图
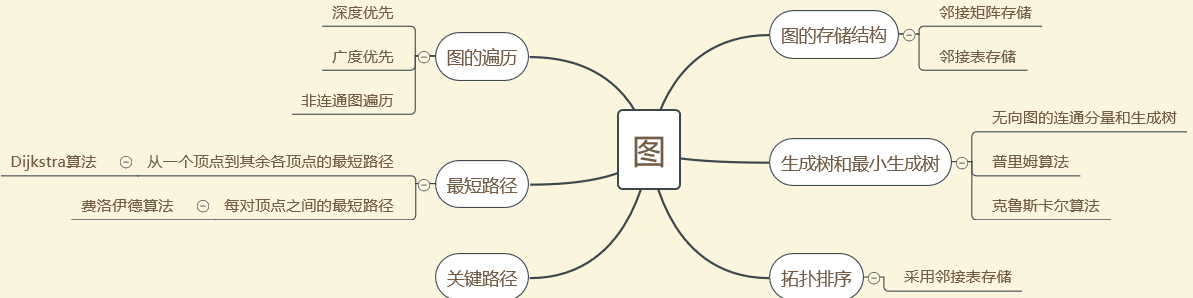
2.谈谈你对图结构的认识及学习体会。
深度遍历算法:
1.从图的某个初始顶点v出发,首先访问初始顶点v,然后选择一个与定点v相邻且没有被访问过的顶点w为下一个初始顶点,再从w出发进行深度优先遍历,知道图中与当前顶点v邻接的所有顶点都被访问过为止。
2.采用递归的方法一般采用邻接表存储结构
3.时间复杂度为O(n+e)用邻接矩阵时时间复杂度为O(n*n)
广度遍历算法:
1.先访问初始顶点v,接着访问顶点v的所有未被访问过的邻接点,依次类推,直到图中所有和初始顶点v有路径相通的顶点都被访问过为止。
2.采用循环嵌套方式以邻接表为存储结构,通过一个队列的出入队来标记是否访问过。
拓扑排序算法
1. 与深度遍历结合可以检测是否产生环路
2. 在一个有向图中找到一个拓扑序列的过程(有向无环图)
2.PTA实验作业
2.1.题目1:图着色问题
2.1.1设计思路(伪代码)
int main(){
定义变量
输入所需要处理的颜色分配scanf("%d%d%d",&v,&e,&k);
for(int i = 0;i<e;i++){
输入
对应入栈}
scanf("%d",&num);
while(num--){
bool flag = true;
清零初始化
for(int i = 1;i <= v;i++){
scanf("%d",&color[i]);
读入着色}
if(不符合图着色对应要求)
flag = false;
for(int i = 1;i <= v;i++){
for(int j = 0;j < mp[i].size();j++){
双重循环判断邻接矩阵存储模式下的图颜色}}
if(!flag)
break;}
根据flag值 输出是否符合条件}
return 0;}
2.1.2代码截图
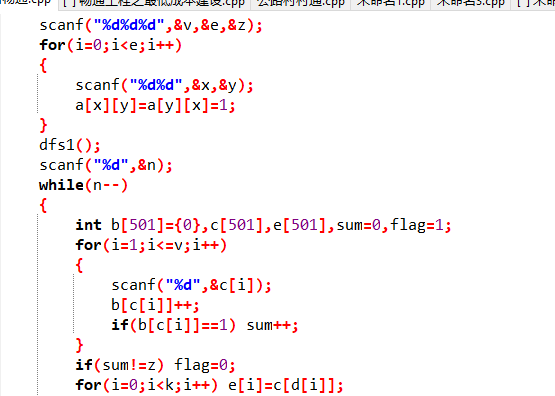
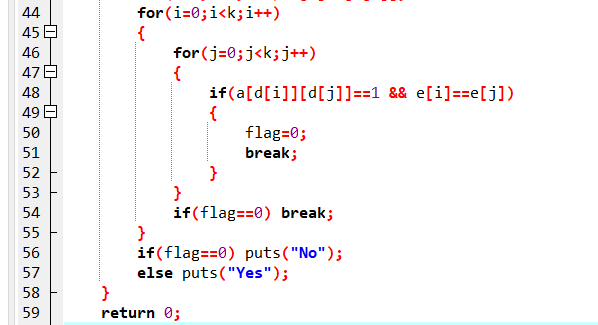
2.1.3本题PTA提交列表说明

2.2.题目2:拓扑排序
2.2.1设计思路(伪代码)
int 定义num数组 ,count表示邻结点数 st为栈数组
int 定义栈顶指针top为-1
for(i从1到n)
将领接表的结点的邻结点都置为0
for(i从1到n)
p指向第一条边
while(p不空)
计算各结点的邻结点数
for(i从1到n)
if(某一结点的邻结点为0)
将此时的i入栈
while(栈非空)
i=栈顶元素
top--
将i的值赋给num【count】 ,并且count++
p指向邻接表的第一条边
while(p不空)
j=p指向终点的编号
j的邻边数-1
if(当j的邻边数等于0时)
入栈j
p=p->nextarc p指向下一条边
if(count==G->n) 即最后结点为0的数等于原来的总结点数
证明拓扑排序完成
for(i从0到count-1)
输出num数组
else
代表拓扑排序还未完成
2.2.2代码截图
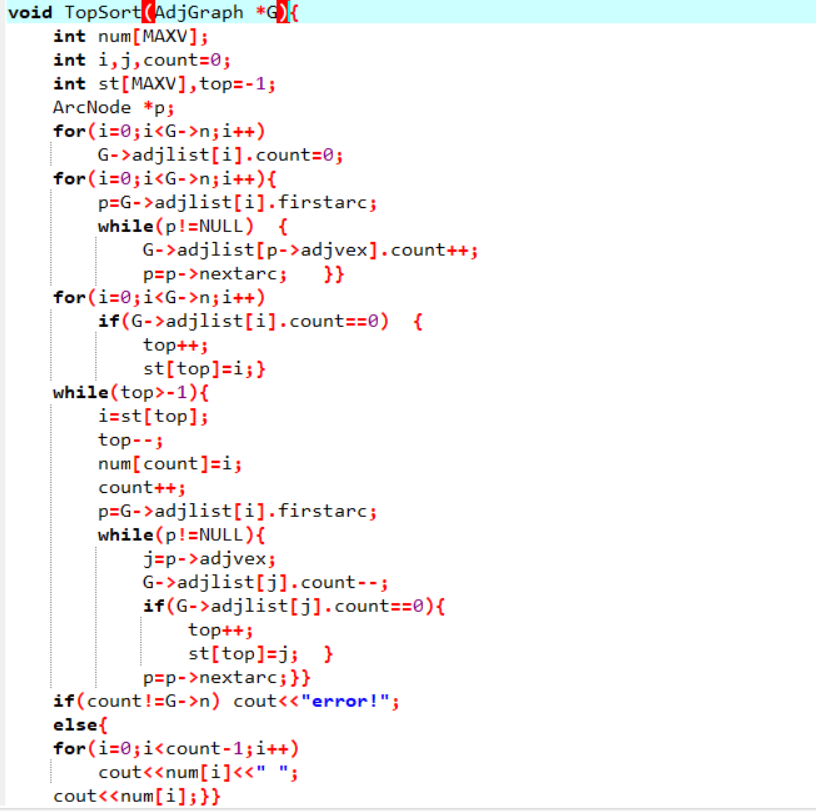
2.2.3本题PTA提交列表说明。
2.3.题目3:六度空间
2.3.1设计思路(伪代码)
int i, vis[10001] = { 0 };
int last = z 记录每层的最后一个元素:该层压入之后弹出之前更新:last=temp;
int tail 用于记录每层压入时的结点
queue<int>q 用到队列的类
q.push(z) z入队
vis[z] 表示z遍历过
while(队列q不空)
z=q.front 重复把队头赋给z
q.pop() 队头元素出队
for(i从一到v)
if(g【z】【i】==1并且 vis【i】==0) 两结点有链连接并且i未遍历过
count++
vis【i】==1 将vis【i】置为1,即遍历过
q.push(i) 将i推入队列
if (last == z) 一层全部弹出,准备开始弹下一层:弹出的(x)=当前层最后一个元素(last) {
level++;
last = tail; 一层全都压入完后,更新last
if (level == 6) break; 如果level达到6了退出循环
return count
main函数里面就是输出格式以及将结点之间通过邻接矩阵连接起来
2.3.2代码截图

2.3.3本题PTA提交列表说明。

3、上机考试错题及处理办法(-2--2分)
3.1.截图错题代码
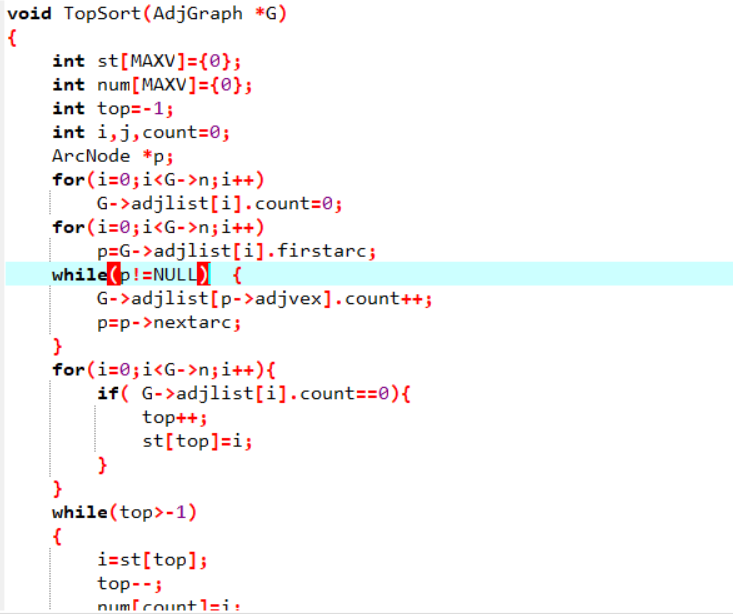
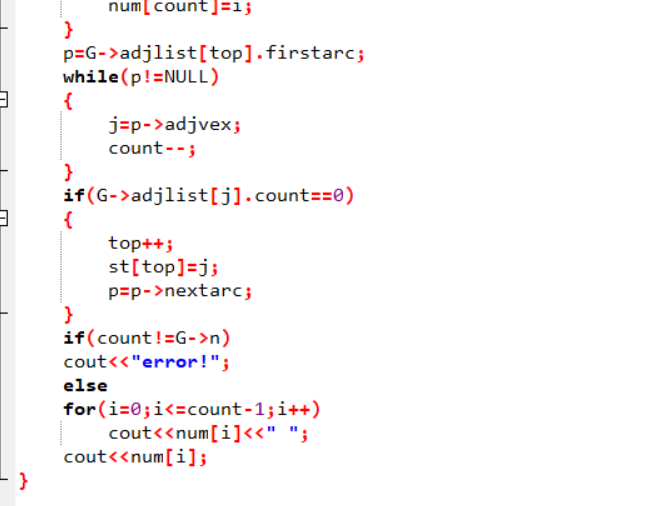
3.2 错的原因及处理方法
错的原因
在while (top>-1)循环里面 count应该递增,并且将p指向第一条边
并且下一个if 不应该包括p=p->nextarc 因为不论是否满足if都应该指向下一个结点
解决方法
在while循环里加上count++ ;p=G->adjlist[i].firstarc
将下一个if中的p=p->nextarc 移到括号外