应用统计学
数据的概括性度量
集中趋势
Mode众数是唯一描述无序类别数据,由图可知众数便是图形中的峰。


对于类别变量,众数就是某一种类别。
中位数和平均数都可能不是样本中的值。
中位数不受极值影响,对于类别数据来说,中位数是某一类别(同mode),各变量值与中位数的离差绝对值之和最小,与均数不同。
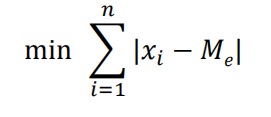
平均数的求法,令函数等于各变量值与平均数的离差平方之和,该函数表达如下式。
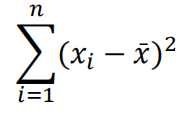
对该函数求一阶导,如下式,
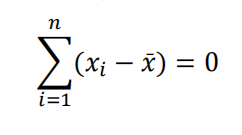
当一阶导为零时该函数取到最小值,此时样本均值表达式为:
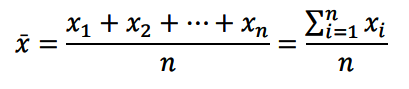
各变量值与平均数的离差平方之和最小,各变量值与中位数的离差绝对值之和最小。两性质验证如下表:
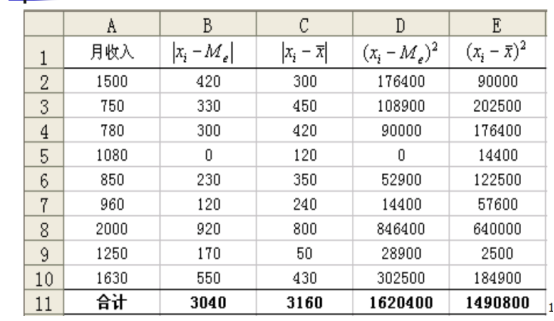
平均值可代数计算且无偏有效,所以数学属性比中位数好。
四分位数中上下四分位数有不同算法,算法的准确度也不同,但是n变大则各算法之间差距变小,同时变的更精确。
几何平均数推导:由以下公式转换,其中x值为比率。
100(1+G)=100(1+x1)(1+x2)(1+x3),等式变换之后得到G的表达式,该G值即为

应用:一种测量多次的平均数比一次测量更准确,样本均值的方差比随机变量的方差小,更准确。所以用样本均值的分布比总体分布的方差小。样本均值方差是总体分布方差/n.
离散趋势
因为平均值不能代表大多数情况,所以引入描述离散程度的特征值。
异众比率即与众数不一样观测值的比率,如下式。
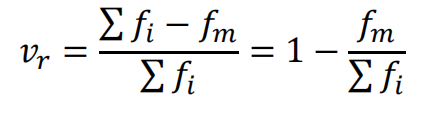
如果异众比率大,则其代表性不是很好。
四分位差:inter quartile range,即3/4处值-1/4处值。
极差:未考虑数据分布
平均差:离均差总和除以总数
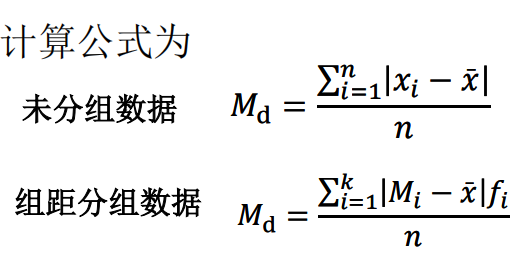
方差&标准差
为什么样本方差的分母为n-1?
若使用n作为分母,则用样本方差估计总体方差有偏。若使用样本方差则无偏。

2.自由度degree of freedom:指数据个数与附加给独立的观测值的约束或限制的个
数之差,即n-(约束个数)。所以就此例可知,要求样本方差,但其中除已知特征值外,还有一个样本均值的约束,所以样本方差的自由度为n-1。
除此之外还有变异系数,消除了数据水平高低和计量单位的影响。
偏态和峰态
偏态系数即表现数据分布的较正态分布的偏斜程度:

峰态系数即表现与标准正态分布比峰值的高低:
