卷积神经网络

一.图像（Image）

1.图像是人类在视觉方面对外界信息的表示，图：光的分布；像：图在人脑中的描述或认识。图像可以简单理解为人眼中画面，可以表示二维或三维信息

2.图像分为模拟图像（像素点无限稠密，连续函数）和数字图像（像素点有限且为离散数值），明显，现在计算机能够处理的只能是数字图像，

3.数字图像：以像素为基本元素，一个图像由有限个像素点组成（矩形点阵），二维图像的大小（height,weight）是指在高（宽）方向有多少个像素点，一个（28,28)的图像在宽、高方向分别有28列像素点，则该图像一共有28*28=784个像素

4.像素pixel：每个像素点在计算机中表示是在离散空间中的一个值，一般为整数，一个像素一般是二维图像中的一个小方格，包含位置信息和光亮度信息

5.数字图像分类

（1）二值图像：一个像素1bit存储，只有黑白两种颜色，用1表示白色，0表示黑色

（2）灰度图像：一个像素8bit（1字节）存储，用黑色来显示物体，以黑色为基准色，亮度从深到浅，0表示黑色，255表示白色，0-255表示不同亮度

（3）RGB图像：一个像素3字节存储，由3个灰度图分别结合洋红（Magenta）、黄（Yellow ）与青（Cyan ）三个通道组成，原因是这三种颜色任意比例混合可以得到任何一种颜色，也就是说：三通道的图像只是表示亮度的强弱，而加上rgb三原色可以显现为彩色图像，此时亮度相当于颜色比例

二.卷积（Convolution）

1.数学上的卷积：是一种两个函数间的数学运算

（1）卷表现为相同的重复，积表现为（范围内的）积分，若是离散的，也就是加权叠加。

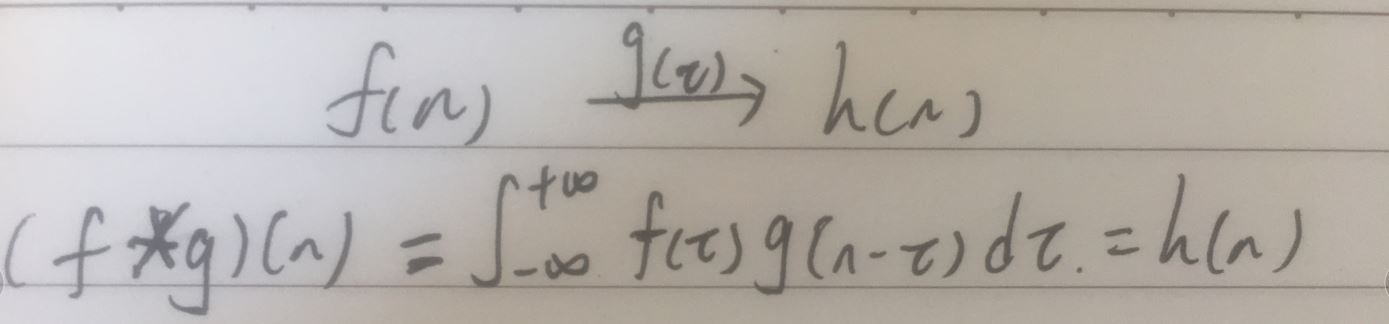
【1】解释：对于一个稳定的系统f，给予一些冲击g，这些冲击会对这个系统造成改变，这个系统在某个时刻n的状态由稳定的状态f(n)变为受到之前一旦时间所有的状态f以及对应每次冲击g的双重影响h(n)，把这段时间可以看做一个个独立的近似无穷小的时刻(负无穷~正无穷)，这和积分的概念一样，相当于当前时刻n的状态是由之前每个时刻的状态和对应冲击共同影响的(f*g)(n)。若是离散时间段，则就是相乘叠加，这大概就是‘积’的概念---每步的输出受到之前每步输入和对应冲击的共同影响

【2】又由于每个时刻设定的受到的影响范围都是一样的，即每个时刻受到之前相同时间段内状态和冲击的影响，即表示每个时刻其实是一样的，平行的，类似于平面上的平行线（斜率一样）（类似卷布），这大概就是‘卷’的概念----每一步都是重复进行的，每一次运算的规则都一样

【3】关于数学上要做g的翻转，可能是因为g的作用是对于第n时刻来说的，也就是只需要受到第n时刻之前的冲击影响，不需要考虑对第n时刻以后的影响，所以做了约束g(n-t)

2.卷积网络中的卷积：用于处理图像，提取特征

（1）二维图像的卷积运算：原图像上和卷积核一样大小的局部像素点阵与卷积核进行卷积运算（矩阵点乘、内积、数量积、元素相乘求和），得到一个像素点的值。因此可以把一个卷积核看做一个窗口，在原图像上滑动进行卷积运算，可以生成一张新的图像

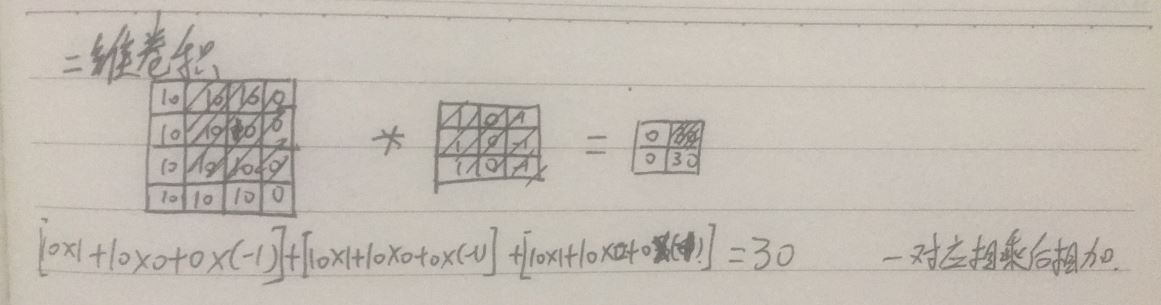
（2）多通道图像的卷积：对原图像使用多个卷积核进行卷积，每个卷积核的参数不一样，每个卷积核不一样，每个卷积核的通道数和原图像的通道数一样，每个卷积核和图像作卷积运算得到一个通道上的二维图像，卷积核数目就是输出图像的通道数数目

 

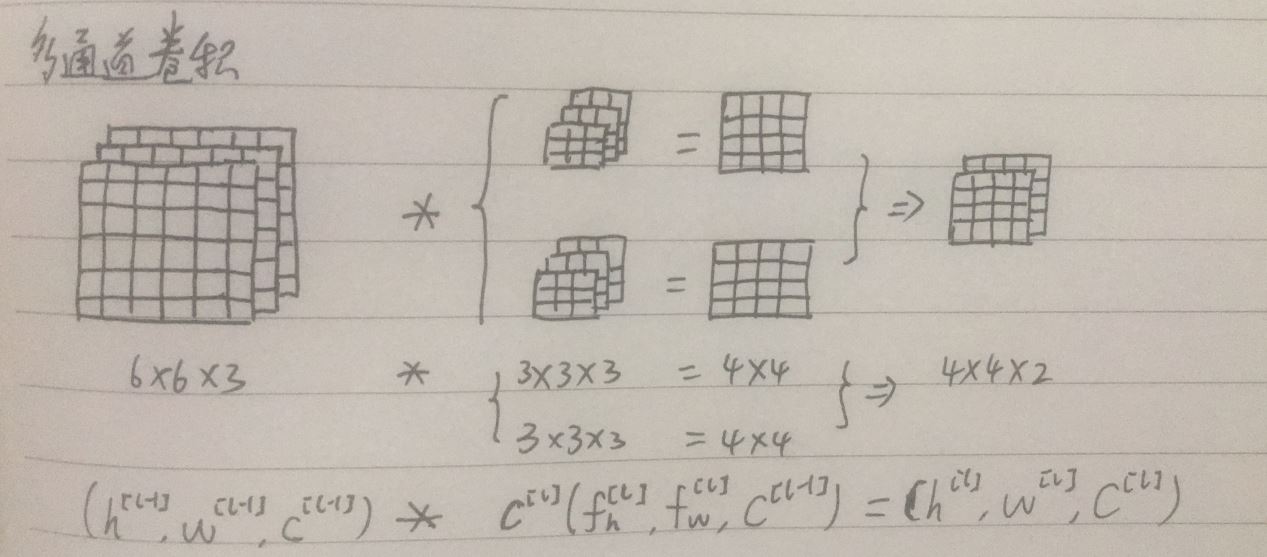
 （3）一次卷积操作：一次卷积包括卷积操作以及激活函数的操作，非线性激活函数是必须的，单次卷积注重于对局部特征的提取

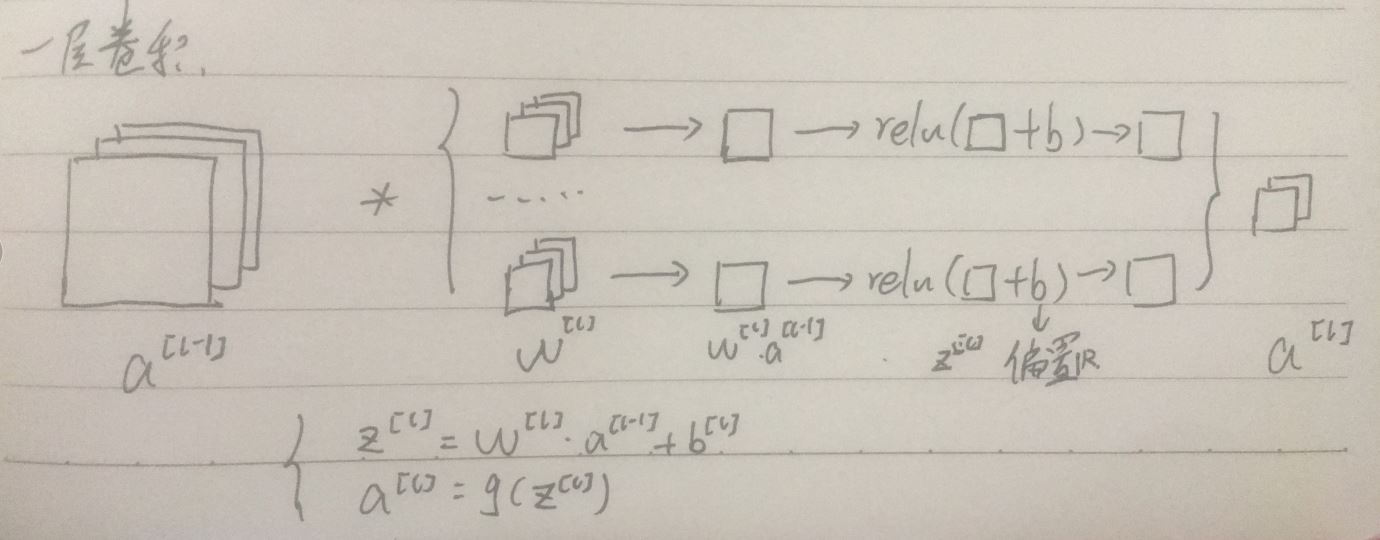
（3）卷积神经网络中的一层：卷积网络中的一层卷积指卷积层和池化层（因为卷积层通常统计具有权重和参数的层），卷积层负责提取局部特征，增加通道数，池化层负责缩小图像尺寸

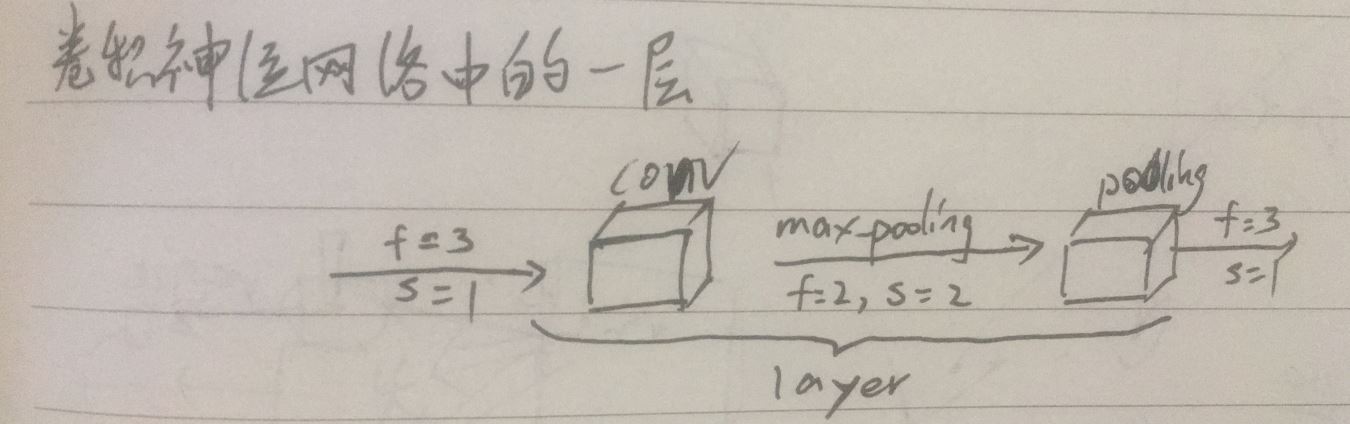
（4）卷积神经网络：

【1】图像的表面包含了众多可见的信息（比如：线条，颜色等），以及需要人进行分析提取才能得到的隐含信息（比如：人的动作，表情等），卷积神经网络是模拟人脑的，人脑对信息的处理也分层（6层？），最外面的大脑皮层接受外界输入--最直观的图像，通过一层层神经元的处理，到最后得到深层次的信息--人的行为心理，这就是人类的认知，而且，有关研究证明：相比于其他动物，人类的神经元层数明显多于其他动物，而且更复杂，灵长类动物的神经元层数也比其他动物丰富，这说明人类与动物的差别在于认知，人类能挖掘出更深层次的信息，那问题来了，又有证明表示人类对大脑的开发不足，若人类要进化，则必须要先开发大脑，提高认知能力.....

【2】卷积神经网络模拟人脑，一般而言，层数在5-7层的效果更好（效果的好坏是人根据自身定义的，上限为人类的认知上限，所以，过多层数显现出来的‘差’的效果，说不定，是人脑不能理解，但是是更深层次的抽象信息，若我们通过不断归纳总结来理解这些信息，是不是相当于对人脑进行有效的开发？而且，不同人有不同的认知只是由于每个人的经历不同，也就是说每个人获得的输入不同，导致最后训练的人脑参数不同，若能获取这些参数和网络模型，输入进机器中,人类也就......），输入一个图像，通过不同卷积核过滤出不同特征，一层层对低级特征进行抽象，得到最终的高级特征，卷积网络的训练是对卷积核的训练，为了得到我们想要的特征，而不是什么特征都能够拿来使用，因为我们有标签，有目标。

三.通道（channel）

1.每个通道有一张灰度图，其中像素大小表示亮度的强弱，0表示暗，255表示亮，三通道可以用rgb三种颜色进行渲染，使得呈现给我们的图像是彩色的，而多通道无法具体呈现

2.卷积网络中，通过卷积操作到最后，每个通道的值或图像是由卷积核进行卷积操作，一层层过滤特征得来的，也就是说到最后，每个通道的图像代表一种局部特征，因为卷积核过滤掉了其他特征

3.一般而言，每层卷积后，卷积核的数量为输出图像的通道数，通道数翻倍，图像大小缩小四倍

（1）解释：每个通道代表一个特征，每个高级特征是前一层低级特征的组合，假设前一层特征有n种，则该层的特征组合最多有2**n中，因为每种低级特征有可以取或不取两种选择，也就是说通道数可以达到2**n个，通道数越多，网络的效果更好，但是，现在的算力不够，所以通道数不能取那么多

（2）其二，一般而言，每层卷积后图像的尺寸在H方向变为原来的二分之一，在W方向变为原来的二分之一，也就是一层卷积后，每个通道图像的大小缩小了成原来的四分之一，我们做卷积网络的目的是使得每次卷积后，整个图像的大小要变小，最终得到一个值或几个值 ，所以一般限制通道数的增长不能超过四倍，一般设置通道数为原来的两倍，当然也可以设置其他值，比如变为原来通道数加一个固定值等等

四.过滤器filter（卷积核函数kernel）（特征feature）：一个包含长、宽、深三个属性的的三维张量（长方体），用于和输入的多通道图像作卷积运算

1.名称解释：

（1）过滤器：卷积核对输入进行卷积运算，得到我们想要的特征，也就是说卷积核能够过滤掉我们不需要的特征

（2）核函数：核函数是指用一个函数代替两个函数的内积，和卷积的定义相似

（3）特征：卷积核用来特征提取，本质上也是一种特征（万物皆可特征）

2.注意

（1）一层卷积，有多少个卷积核，输出图像就有多少个通道，而且这些卷积核都不一样，需要反向传播计算梯度更新卷积核参数，卷积核中每个元素对应一个权重参数，即模型通过训练数据自动找到好的过滤器，学习想要的特征

（2）每个卷积核的深度和输入图像的深度一致，卷积计算是所有对应元素相乘求和得到一个像素，通过滑动窗口的方式得到一个输出图像

（3）卷积核的长宽一般相等，卷积核大小越大越好，当和输入同大小时，就变成全连接了，但是带来参数巨多、训练难的问题，当为1时，不考虑周围元素，卷积后图像大小不变，通常用于改变通道数，是对特征的重新线性组合，就是对原图中的一个像素点的所有通道的线性变换。卷积核大小一般为奇数，比如3x3、5x5...常用3x3（已证明比5x5好：一次5x5的卷积，相当于两次3x3，同时参数个数由5x5xn变为2x3x3xn,减少了百分之28，而且，两次3x3比一次5x5更注重局部特征的提取，所以一般用3x3）,卷积核大小为奇数是因为

【1】只有一个中心像素点会更方便，便于指出过滤器的位置;

【2】为了便于对称填充padding

（4）同一通道上所有像素点所用的卷积核一样，卷积参数一样，卷积窗口不一样

（5）坐标相同，不同通道的像素点卷积窗口一样，但卷积核不一样，卷积参数不一样

（6）卷积核越大，效果越好，特征越抽象，但带来计算的相关问题

五.步长stride：每次操作，过滤器窗口滑动的距离，整数，最小为1

1.步长一般不大于卷积核大小，若步长太大，则会有一些特征未能被有效提取，若步长太小，提取特征会很全面，但是计算量也大，

2.步长也分上下和左右两个步长，用元组表示，一般在长和宽两个方向的值，行进顺序是从左往右，从上往下，过滤器不超出图像

3.s=1的过滤器更注重局部特征的学习，一般用于卷积操作，而s=2的卷积表示跳格平移，用于减小图像尺寸，一般用于池化层

六.填充padding：一般在卷积的开始前进行边缘扩充

1.为什么要padding?

（1）卷积是在图像里进行的，一般而言，卷积核大小大于1，这就导致边缘的点和中间点的卷积的不公平，这就会导致丢失图像边缘的一些信息，所以在卷积前在图像边缘添加一层层像素点就有了意义，使得边缘的点能像中间的点一样，参与多次卷积运算

（2）若不填充，由于卷积元素设定不超过图像，则当卷积核大于1时，图像尺寸经过卷积后必然减小，也就是丢失了部分信息，这与我们期望不符

2.padding常用模式

（1）'valid'：不填充

（2）‘same’：填充padding，使得填充后，使得原来按步长卷积后需要丢弃的像素，可以在补padding后参与计算，即：当步长为1时，输入和输出图像大小一致；当步长为2时，输出图像的大小为输入图像的一半...

3.注意

（1）我们添加padding像素点，是表示一层层的添加，而且最好是对称添加，若是奇数，多出1，则约定：左边比右边少1，上边比下边少1

（2）卷积的图像是padding之后的图像，而不是padding之前的图像

（3）padding的大小可以表示单边添加的层数，也可以表示双边添加的层数，这需要指明

七.激活函数

1.激活：现实中是指人脑神经元的激活，在神经网络中是指映射变换。卷积神经网络中一般使用relu非线性函数

2.和神经网络加入激活函数原因一样，添加非线性变换使得神经网络拟合能力更强，拟合多折线（曲线），（举例：若是全连接，则样本点之间用直线

（1）补充：非线性变换对神经网络的影响：二维空间中，神经网络的实质是用线来拟合样本点，若是一个输入，一个神经元，一个输出的网络，则它的数学表达式为y=ax+b，这表示用一条直线拟合每两个样本点，若加了relu函数，则表示用一个斜率任意的二折线来拟合每两个样本点，当该层神经元数增加1时，表示进行了两次二折线操作，即把这两条二折线叠加，用有一条三折线来拟合每两个样本点，同样，n个神经元就表示用一条n+1折线拟合两个样本点，最多有n个折点。而若是sigmoid函数，则表示用曲型拟合每两个样本点，极端情况sigmoid变成弓型拟合（梯度消失时），这反而造成了拟合的难度

（2）样本数和神经元数相同时，网络拟合的是每两个样本点之间的连线，单次全连接参数的个数，是此次折点数目的上限，当在多维空间时，使用超平面进行拟合，神经网络实质就是通过大量样本统计归纳规律，训练的实质就是拟合已知样本点，目的是对于未知样本点，找到其相邻样本，从而进行预测等操作

（3）补充：模型崩溃：参数发生一点更改，模型的结果变化巨大。原因：多维时，参数的微调可能导致相邻点的剧烈变化，从而导致模型结果通过训练发生巨大改变

3.常用激活函数

（1）sigmoid：反向更新梯度时，梯度最大为原来的四分之一（0时），这就导致更新几步，用链式法则求梯度后，梯度会趋向于0，到达饱和区，导致梯度消失，而且，在训练时，还应对输入作归一化处理，所以，一般不用其作为卷积后的激活函数，常用于做最后输出时求解一个概率值

（2）relu：常用于卷积层激活函数，计算简单、无梯度消失的问题，但是，当为负值时，激活值0，负梯度为0，可能会导致一些节点‘死亡’，网络变稀疏，所以应把lr设置的小一下，使得其变化地不那么剧烈；其二，当参数变大时，由于链式法则反向更新梯度，也有可能会导致梯度爆炸，

八.池化pooling：考虑到相邻特征可能具有某些关系（比如相邻像素点相似--衣服单一颜色），同时某些特征是我们不需要学习的（特征冗余），则我们可以用一个点特征来代替一块区域的特征，也就是池化操作

1.常用池化

（1）最大值池化（max pooling）:计算图像区域的最大值作为该区域池化后的值。排除一些不需要的特征，保留纹理信息，最常用

（2）均值池化（Average pooling）:计算图像区域的平均值作为该区域池化后的值。保留图像的背景信息，容易造成特征稀释（一大一小取均值时）

2.优缺点

（1）优点：

【1】简单，无可训练模型参数，只是单纯的计算，一般有两个超参数：过滤器大小f和步幅s，所以减少了网络的训练参数，减少了计算量

【2】池化层一般在卷积层之后，保留主要特征，去除冗余特征，减少了卷积层输出的特征数，变相地增加了下层卷积核的感受野，也就减弱了特征过多带来的过拟合问题

（2）缺点：实际上pooling层丢失了一部分信息，可能会导致一些问题

（3）本质：采用pooling通常是为了减少一半的图片尺寸，计算时尽量不重叠，通道数不变，本质上是进行了特征选择(保留主要特征，去除冗余特征)，

（4）关于梯度：反向计算梯度时，有值的地方才有梯度，均值池化的梯度要除以卷积核元素数量，也就是梯度之和不变

九.其他

1.卷积实质：积分运算的离散实现，用以挖掘图像中的特征

【1】单次卷积是全连接操作的一种特殊情况，是线性的，是对图像局部特征（一些像素）的处理，将其转换为一个稍大一点的‘局部’特征（一个像素），局部的大小由卷积核大小决定

【2】每一个卷积核对一个图像作的卷积是对整个图像进行特征过滤，为了提取自己想要的关于图像的一个特征（一个通道）

【3】每一层卷积就是对图像中的各个特征的提取，多个通道代表多个特征，输出的多个特征间相互独立，因为参数不一样

【4】卷积神经网络：通过一层层卷积，得到最终想要的特征，

【5】卷积网络的训练：通过输入相似图片，进行卷积后，得到抽象的特征，将低级特征抽象为高级特征，是一种总结归纳，统计规律，比如：很多有实际人脸的图像，通过卷积后，得到‘人脸’这一个概念--有眼睛、嘴巴等，要抽象出什么特征取决于我们的目的，也就是标签，再通过不断优化参数得到最终能够提取我们想要特征的过滤器

2.经验：一般5-7层卷积最佳，单层最佳组合：卷积层（f=3,s=1,'same'）+池化层（f=2/3,s=2），卷积层注重局部细节特征的学习，池化层注重全局特征的选择，两者的组合相当于使用一个更大的卷积核进行卷积操作

3.参数共享：卷积核提取的是特征，它本身也是一种特征，也就是说，无论对于图像哪里，它提取特征这个特性是不会改变的

4.相关计算

十.卷积网络结构

1.经典卷积网络结构：自己设置参数

（1）输入：对于一张3通道的图片，关于图像尺寸，没有要求，但有时可能需先resize到我们需要的长宽一致的尺寸，比较好处理，比如224x224，再输入到网络中，而且输入尺寸最好为2**n的倍数（比如：若卷积5层，最好输入32的倍数）

（2）第一次卷积：需先将3通道的图像卷积为偶数通道的图像，比如64,32,16...

（3）中间卷积层：每层卷积都是一层卷积操作用以提取局部特征（f=3,s=1,'same'），全连接操作参数多，容易过拟合，卷积不容易过拟合，池化操作用以缩小图像尺寸，关注全局特征(s=2,f=2/3,max_pooling)，这样，每次卷积后图像通道数增一倍，图像尺寸变为原来四分之一，通常4-5层卷积层

（4）输出：将最后的一层的卷积输出先拍扁成向量(flatten)，再进行一些全连接（FC）到我们需要的logits输出向量，根据需求对logits进行处理

【1】若是求一个值，则logits是一个值，若是一个概率值，需再用sigmoid函数将其转为概率，损失计算是将其直接与标签比较

【2】若目标是求得一个多维向量，则logits是一个向量，若是算几个概率，则需用softmax函数将这个logits向量变为概率向量，此时，若标签是一个值，则需先转为onehot向量，损失计算为概率向量与onehot向量在每个维度上的差距求和

【3】拍扁+全连接=全局卷积，全连接层在cnn中起到‘分类器’的作用，因为卷积层是注重从局部到整体的特征提取和组合，得到的每个特征是关于整个图像的一个全局特征，注重图像的全局信息，这些全局特征都是相互独立的，而且未能体现各个全局特征在图像中的空间位置信息，因此要将它们组合起来，通过全连接得到一个较为完整的、既包含全局特征、又包含位置信息的特征，再将其全连接映射为类别特征，进行softmax分类，比如卷积层得到一些特征：眼、耳、口...而输出的人脸类别具有位置信息，在全连接层将他们进行重新组合，形成真正的人脸特征

【4】另外：全连接：指下一层的每个节点都与上一层每个节点有关，在CNN中则是图像与和图像大小一样的卷积核作卷积，CNN中的全连接层是把图像拍扁再作全连接，实质是特征组合；全卷积网络就是把CNN后面的全连接层变为卷积层，但不要求图像尺寸，是局部特征的组合

（5）局部连接：每个输出值只与部分输入有关；共享参数：一个卷积核用于一整张图像，提取各个局部特征

2.残差网络（ResNets）(Residual Networks)：残差捷径

（1）相关概念：

【1】误差：观测值与真实值的差距；偏差：个别观测值与观测均值之间的差距；残差：观测值与预测值之间的差距；损失：预测值与真实值之间的差距

【2】一般而言，真实值是不知道的，观测的目的是为了得到真实值，我们用多次观测的结果统计规律得出的值代替真实值，也就是说有时把观测值代替真实值

（2）结构和改变

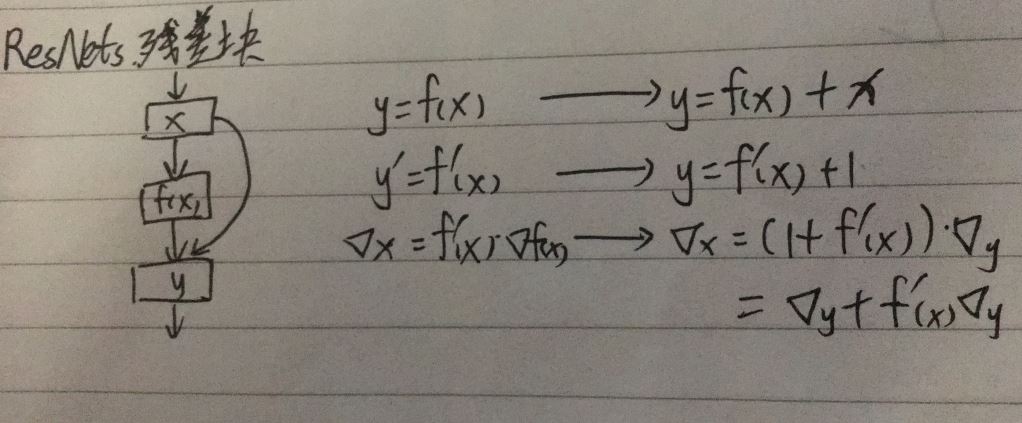
（3）特点：

【1】从梯度角度，本被可能导致的梯度消失的问题不容易发生，从而解决梯度消失问题，而且根据梯度反向传播的原理，一个残差块其实就是一层的传播，也就解决了网络过深带来的训练效果差的问题，它所真实的层数其实很小，一个残差块只是一层

【2】从模型角度，就是在本身网络层与层之间加入了一些残差学习层，为了学习原来网络没有学到的信息，所以一般而言，增加了残差学习的网络效果比原来更好，而且，若跳转学习的错误率为e1，残差学习的错误率为e2，则整个模型训练的错误率变为两者都出错的概率e1*e2，模型犯错的概率降低，类似于集成方法思想（GBDT）

https://blog.csdn.net/u013181595/article/details/80990930

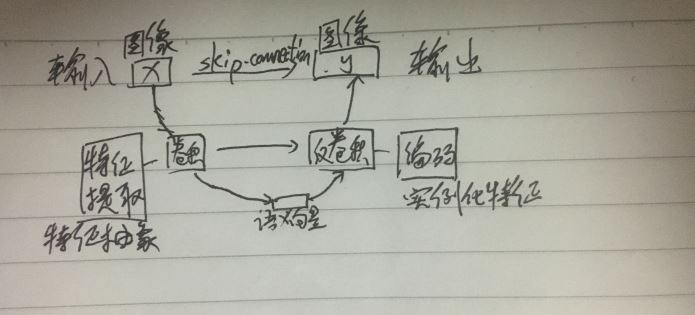
3.Unet：图像到图像

（1）特点

【1】输入一张图片，输出一张图片，整个网络看上去是对称的，和生成模型类似，先将输入图像进行特征提取，也就是编码过程，再利用反卷积进行解码操作得到输出图像，为了防止信息的丢失，还加入了skip-connection

（2）skip-connection：在用特征抽象后得到的语义向量（高级特征，全局特征）还原到和原图相关的图像（低级特征，局部特征）时（先确定整体，再确定局部），实例化特征时可能带来信息丢失的问题，也就是和原图像关联程度低，所以加入了skip-connection，也就是说，把encode时得到的特征图和decode时的特征图对应，在编码阶段保存特征图（堆栈），在解码阶段，将堆栈中的特征图加入其中，得到对应的解码时的特征图

（3）反卷积（转置卷积）：是一种特殊的卷积，通过一定的补0，扩大图像尺寸，但是不能还原数值

（4）常用于语义分割、实例分割，图像增强、性别变换等，不加全连接fc

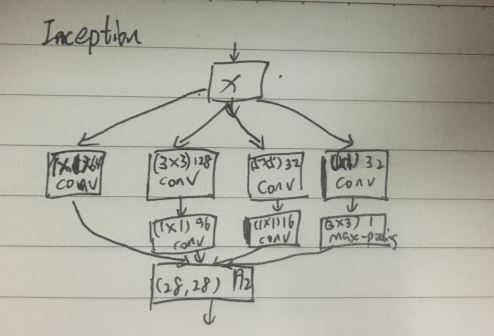
4.Inception：图像到图像

（1）特点：让网络代替人工来确定使用什么卷积核和池化层相关组合

【1】引入1x1卷积改变通道数，对特征重新组合

【2】通过增加网络的宽度丰富每层的信息，来提高网络性能

【3】让原图经过各种操作后，根据通道feature将他们的结果concat组合起来，

【4】适用于大特征和小特征同时存在的图像，常用于人脸检测，要跟fc

十一.应用方向

1.应用：卷积神经网络将低维特征抽象为高维特征，使用的映射思路是不断提取局部特征从而得到全局特征，多用于图像，可以应用于语音、文本等

2.图像分类（image classification）：识别图像内容

（1）流程

【1】输入：一些图片，可能带有类别标签，这个标签的表示可能是一个值，可能是一个语义，也可能是一张特征图。一般一张图片对应一个类别标签，也可能一张图片对应多个标签，这一个数据集可能有多个类别，将其放入cnn中训练

【2】输出：输出的类别标签，和给定真实标签作损失计算，反向梯度更新参数，注意：输出可能是一个值，也可能是多个值，有时要用softmax

【4】预测：给定一张图片，可以通过训练所得的网络后，输出它的类别

【5】目标：预测一张图片的类别

（2）应用：图像识别、人脸验证

（3）人脸识别：

【1】问题：有一个人脸数据库，输入一张人脸，若数据库中只有一张或没有该人脸，该怎么判断？重新训练模型在现实中是不可能的。解决：生成每个人脸的语义向量，将这张人脸的语义和数据库中每个人脸语义进行比对，低于某个阈值，表示这两张图片是一样的

2.图像分割：理解图像各个像素的意义（类别），画语义或实例的轮廓，轮廓不会交叉或重叠

（1）语义分割(semantic segmentation)：语义就是类别，对图像中每个像素点进行分类，得到每个类别物体的轮廓

【1】是N+1的对于每个像素的分类问题，N表示图像中的所有类别总数，1表示背景，对于每个像素进行预测分类，从而分割出不同类的区域，可以把同一类物体的轮廓标注出来----若有两个物体是同一类而且连接在一起，则会判别为同一类物体，轮廓也是这两个物体的外轮廓

【2】常用方法：类似于UNet，先用卷积从原图中提取抽象特征，再用反卷积映射为一样大小的类别图像，并标注对应物体类别，从而知道原图上有什么，在哪里，像素之间完全映射，

（2）实例分割：实例就是单个物体，对图像中每个像素点进行分类，得到每个实例物体的轮廓

【1】是N+2的每个像素分类问题，N表示前景中类别总数，2表示背景和边界两类，根据像素分类结果，根据边界，将不同个体分割出来，再用另一个网络进行类别判断

（3）特点：样本难以标注（画轮廓），模型简单，效果好

3.目标检测：图像中物体定位+分类