poj 2828 Buy Tickets 【买票插队找位置 输出最后的位置序列+线段树】

题目地址：http://poj.org/problem?id=2828

Sample Input

4
0 77
1 51
1 33
2 69
4
0 20523
1 19243
1 3890
0 31492

Sample Output

77 33 69 51
31492 20523 3890 19243

Hint

The figure below shows how the Little Cat found out the final order of people in the queue described in the first test case of the sample input.

      问题是这样的：现在有n个人要买票，但是天黑可以随便插队。依次给出将要买票的n个人的数据信息。包含两项：pos,当前第i号人来了之后他肯定要
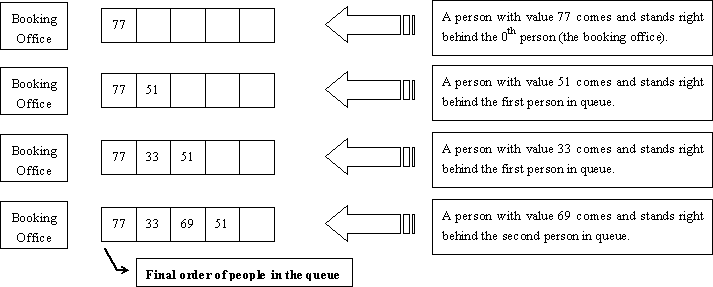
插入到pos这个位置，如果当前pos无人，那最好了，直接把他插入即可。但如果pos这个位置有人了，从现实意义上讲，第i号人插入之后，相当于他

后面的人在原来的基础上都往后挪了一个位置！（ps:这就是为什么人们都讨厌插队的人的原因啊！！！） 每一个人都携带一个val值，当n个人全部确定下

来之后输出val序列。

　　分析：很简单的就可以想到，前面的人虽然先到了，但他的位置并不能确定，因为后来的人完全可以插队到你的位置，而你则后移了一个位置。也即是说，

我们在确定最后的序列时，并不能按照先来后到的顺序处理。我们应该从后往前处理！这样最后到达的人的位置一定是确定的，他的位置绝对是一次就确定的。

同理往前递推处理。

　　算法结构：采用线段树，每一个节点存储的是当前区间的剩余空位置。

     

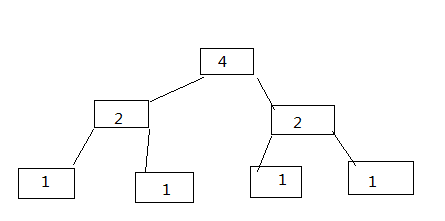
注意一个地方：线段树的下标是从1开始的，而买票的这些人的插队位置是从0开始的，所以理应在查找更新时pos要加1，如果不加1则在判断往哪个子节点

移动的时候是>pos

code:

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
#include <math.h>
#include <iostream>
#include <algorithm>

using namespace std;


struct seq
{
    int pos, val;
}a[200000+10];

int num[800000+100];
int ans[200000+100];

void Build(int rt, int ll, int rr)
{
    num[rt]=rr-ll+1;
    if(ll==rr)
        return;//已经到达根节点
    Build(rt*2, ll, (ll+rr)/2 );
    Build(rt*2+1, (ll+rr)/2+1, rr );
}

int update(int pos, int rt, int ll, int rr)
{
    num[rt]--;//空位置数量-1
    if(ll==rr)
        return ll;//到达根节点
    if(num[rt*2]>pos)//pos是从0开始的 而线段树是从1开始存储的 但0和1在此题中是对应存储的
        return update(pos, rt*2, ll, (ll+rr)/2);
    else
        return update(pos-num[rt*2], rt*2+1, (ll+rr)/2+1, rr);
}

int main()
{
    int n, i;
    while(scanf("%d", &n)!=EOF)
    {
        for(i=0; i<n; i++){
            scanf("%d %d", &a[i].pos, &a[i].val);
        }//打表保存
        Build(1, 1, n);//从1号节点开始建树 区间[1,n]

  /*      for(i=1; i<=7; i++)
            printf("%d---", num[i]); */

        for(i=n-1; i>=0; i--){
            ans[update(a[i].pos, 1, 1, n)]=a[i].val;
            //
        }
        for(i=1; i<=n; i++){
            printf("%d%c", ans[i], i==n?'
':' ');
        }
    }
    return 0;
}