题目:
Given n, how many structurally unique BST's (binary search trees) that store values 1...n?
For example,
Given n = 3, there are a total of 5 unique BST's.
1 3 3 2 1
/ / /
3 2 1 1 3 2
/ /
2 1 2 3
链接: http://leetcode.com/problems/unique-binary-search-trees/
题解:
用DP求catalan number。 Cn+1 = ∑(Cn - i * Ci ), i 的范围是( 0 ~ n)。公式不太好写,改天要用Latex编辑一下。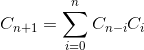 。有机会的话也要好好学习一下解析组合数学 - Analytic Combinatorics。Sedgewick有本书专门讲这个。
。有机会的话也要好好学习一下解析组合数学 - Analytic Combinatorics。Sedgewick有本书专门讲这个。
Time Complexity - O(n), Space Complexity - O(n)。
public class Solution { public int numTrees(int n) { //catalan number if(n <= 0) return n; int[] dp = new int[n + 1]; dp[0] = 1; for(int i = 1; i < dp.length; i++) { for(int j = 0; j < i; j++) { dp[i] += dp[(i - 1) - j] *dp[j]; } } return dp[n]; } }
或者用catalan数的另外一种推导,也是dp。
public class Solution { public int numTrees(int n) { //Catalan number Cn+1 = 2(2n + 1)/ (n+2) * Cn if(n < 0) return 0; int[] count = new int[n + 1]; count[0] = 1; for(int i = 1; i < n + 1;i++) count[i] = (int) (count[i - 1] * 2.0 *(2.0 *(i - 1) + 1.0) /(i - 1.0 + 2)); return count[n]; } }
二刷:
求catalan number, 公式是Cn+1 = ∑(Cn - i * Ci ), 求和的范围是[0, n] 前后闭
Java:
public class Solution { public int numTrees(int n) { if (n <= 0) { return n; } int[] dp = new int[n + 1]; dp[0] = 1;for (int i = 1; i <= n; i++) { for (int j = 0; j < i; j++) { dp[i] += dp[(i - 1) - j] * dp[j]; } } return dp[n]; } }
三刷:
这里要仔细注意一下dp数组的创建以及计算公式时的边界条件。 我们求第n个数的结果的话,其实是wiki公式里的第n + 1个数。所以我们建立一个长度为n + 1的一维数组dp,最后返回dp[n]就可以了。 其中Catalan number公式仍然用的是公式是Cn+1 = ∑(Cn - i * Ci ), 求和的范围是[0, n] 前后闭。所以假如我们要求dp[i], 那么内循环就是计算从0到 i-1 这 i 个数的乘积和。
Java:
Time Complexity - O(n), Space Complexity - O(n)。
public class Solution { public int numTrees(int n) { if (n <= 0) return 1; int[] dp = new int[n + 1]; dp[0] = 1; for (int i = 1; i <= n; i++) { for (int j = 0; j < i; j++) { dp[i] += dp[j] * dp[(i - 1) - j]; } } return dp[n]; } }
题外话:
有空的话还是要学一学离散数学的各种知识。
Reference:
http://www.codecogs.com/latex/eqneditor.php
http://en.wikipedia.org/wiki/Catalan_number