参考资料
1.向量旋转公式
2.旋转矩阵和旋转向量
2.1旋转矩阵微分和旋转向量的推导
2.2罗德里格旋转公式
3.四元数和旋转向量
3.1 由欧拉参数推导四元数
3.2旋转向量表示四元数
4.旋转矩阵和四元数
5.欧拉角和旋转向量角
1.向量旋转公式
2.旋转矩阵和旋转向量
2.1旋转矩阵微分和旋转向量的推导
2.2罗德里格旋转公式
3.四元数和旋转向量
3.1 由欧拉参数推导四元数
3.2旋转向量表示四元数
4.旋转矩阵和四元数
5.欧拉角和旋转向量角
参考资料
- Quaternion kinematics for the error-state KF
- barfoot《state estimation forrobotics》
- 袁信、郑锷《捷联式惯性导航原理》
- 以上书籍的下载链接链接:http://pan.baidu.com/s/1c1G0k5U 密码:jdsz
刚体在空间中的一次旋转可以用旋转矩阵,四元数和旋转向量三种方式表示,以下总结三者的数学转化关系。
1.向量旋转公式
- 旋转向量的定义:方向是旋转轴,大小是旋转角的向量,表示刚体在空间中的一次旋转。
- 定义向量x绕单位旋转轴u旋转角度,将向量绕u轴和垂直u轴分解,并利用向量的点乘的几何意义得到:

- 平行于u轴的分量在旋转中保持不变,垂直分量则旋转角度,公式(48)到(49)的推导利用了正交基的几何关系和上式证明的模长相等。

2.旋转矩阵和旋转向量
2.1旋转矩阵微分和旋转向量的推导
- 相对于笔记1,利用哥氏定理推导旋转矩阵的微分方程,这里给出了另外一种微分方程的推导,并从旋转角时间积分的角度给出一种旋转向量的定义。

2.2罗德里格旋转公式
- 利用李群SO(3)推导出以旋转向量表示的罗德里格旋转公式(Rodrigues rotation formula);其中计算时旋转轴u用哪个坐标系表示都是等价的,后面将证明。
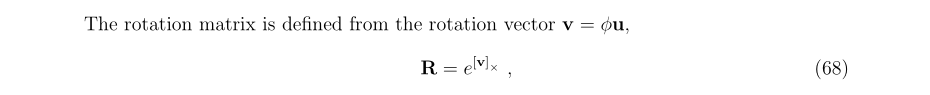

- 利用罗德里格旋转公式推导向量旋转公式
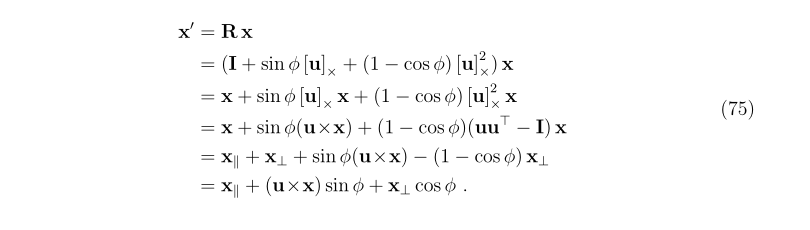
3.四元数和旋转向量
3.1 由欧拉参数推导四元数
由旋转矩阵的欧拉参数(Euler Parameters)推导单位四元数的表示,这里参考barfoot书上的内容,这部分也证明了罗德里格旋转公式的旋转轴u用哪个坐标系表示都可以。1中也有说明,旋转轴在旋转过程中没有几何位置变化。


由此得到以欧拉参数推导出的单位四元数
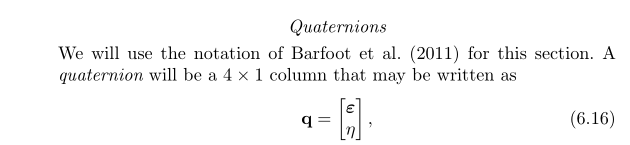
3.2旋转向量表示四元数
- 根据3.1,由旋转向量表示四元数可以写成:

- 用四元数表示向量的旋转,这里和四元数相乘运算的三维向量都改写成四元数的形式(只有虚部,实部为0),并进行了证明(结果等于向量旋转公式结果):

4.旋转矩阵和四元数
- 由2.2和3.3,以向量旋转公式为纽带,得到旋转矩阵和四元数表示旋转的等价关系,进而得到单位四元数的元素表示的旋转矩阵,该结果和3.1由欧拉参数表示罗德里格公式的结论一致。3.1中的欧拉参数其实就是这里的单位四元数的实部和虚部。
- 其中表示这里的x是以四元数的形式表示的。

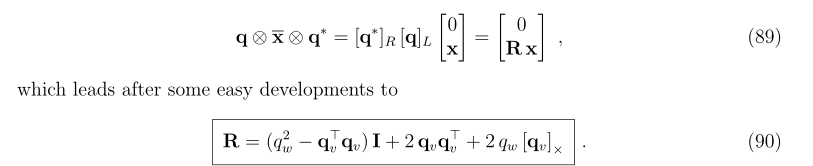
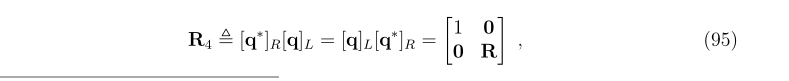
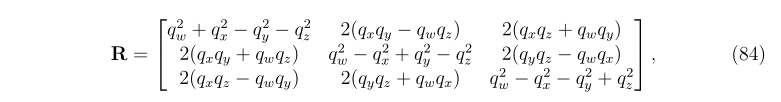
5.欧拉角和旋转向量角
- 我们提到欧拉角,一般指的是绝对姿态的欧拉角,即导航系下的机体俯仰滚转和偏航角,而旋转向量角指的是一次旋转过程的角度,一般是微小量。
- 两者的关系:机体在运动过程中欧拉角的更新可以看做是初始旋转矩阵(欧拉角表示)与每次旋转矩阵(旋转向量角表示)的积分。