本文摘自: http://developer.51cto.com/art/201403/430986.htm
书籍:《啊哈,算法》
高快省的排序算法
快速排序是一种既不浪费空间,效率又很高的排序算法。
现在对“6, 1, 2, 7, 9, 3, 4, 5, 10, 8”这十个数进行排序。首先在这个序列中随机定一个基准数(参照数),可以将第一个数作为基准数;然后,将这个序列中所有比基准数大的数放在基准数的右边,比基准数小的数放在基准数的左边:
3, 1, 2, 5, 4, 6, 9, 7, 10, 8
在初始状态下,数字6在序列的第1位。我们的目标是将6移动到序列中间的某个位置,假设这个位置是k,并且以k为分界线,左边的数都小于6,右边的数都大于6。
排序算法步骤
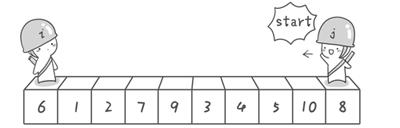
初始位置:分别从待排序队列的两端开始“探测”。先从右到左找到一个小于6的数,再从左到右找到大于6的数,然后交换他们。可以用变量i和j分别表示序列的最左边和最右边,分别起名“哨兵i”和“哨兵j”。刚开始的时候让哨兵i站在序列最左边(i=1处,指向数字6),让哨兵j站在序列最右边(j=10,指向数字8)。
行动方案:首先哨兵j开始出动(此处设置的基准数是最左边的数,所以需要让哨兵j先出动,因为... ...)。哨兵j一步一步向左走(j--),直到找到第一个小于6的数停下来;接下来哨兵i一步一步向右走(i++),直到找到了第一个大于6的数停下来。最后哨兵j停在了数字5上,而哨兵i停在了数字7上。

现在交换哨兵i和哨兵j脚下元素的值。

交换之后的序列如下:
6, 1, 2, 5, 9, 3, 4, 7, 10, 8
至此,第一次交换结束。接下来开始哨兵j继续向左移动,发现了4(比基准数6小)之后停下来;哨兵i也继续向右移动,发现了9(比基准数大)之后停下来。

此时再次进行交换

交换之后的序列如下:
6, 1, 2, 5, 4, 3, 9, 7, 10, 8
至此,第二次交换结束。“探测”继续,哨兵j继续向左移动,发现了3(比基准数小)之后停下来。哨兵i继续向右移动,此时哨兵i和哨兵j相遇了,都站在3面前。说明这一轮探测结束。

将基准数6和3进行交换。


交换之后的序列如下:
3, 1, 2, 5, 4, 6, 9, 7, 10, 8
至此第一轮“探测”真正结束。此时以基准数6为分界点,左边的数都小于等于6,右边的数都大于等于6。回顾刚才的过程,其实哨兵j的使命就是找到小于基准数的数,而哨兵i的使命就是找到大于基准数的数,直到i和j相遇为止。
现在基准数6已经归位,我们以6为分界点拆分两个序列,左边的序列是“3, 1, 2, 5, 4”,右边的序列是“9, 7, 10, 8”。然后分别处理这两个序列。处理步骤与刚才第一轮“探测”相同。
左边的序列以3为基准数进行调整,使得3左边的数都小于等于3,右边的数都大于等于3,调整完后的顺序应该是:
2, 1, 3, 5, 4
现在3已经归位。接下来处理3左边的序列“2, 1”和右边的序列“5, 4”。对左边的序列以2为基准数进行调整,处理完毕之后是“1, 2”,此时2已经归位。序列“1”只有一个数不需要进行处理,同理可对右边的序列进行调整,最后得到的序列如下:
1, 2, 3, 4, 5, 6, 9, 7, 10, 8
对于序列“9, 7, 10, 8”同样模拟以上过程,直到不可拆分出新的子序列为止。最终得到的序列是:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
到此,排序结束。其实快速排序的每一轮处理就是将这一轮的基准数归位,直到所有的基准数都归位为止,排序就结束了。
下面是详细图解:

快速排序为什么效率高?
相对于冒泡排序,快速排序每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放在左边,将大于等于基准点的数全部放在右边。这样的交换不会像冒泡排序那样每次只能在相邻的数之间进行交换,快速排序交换的距离大,总的比较次数少,速度就自然提高了。当然最坏的情况仍可能是相邻的两个数进行交换。因此快速排序最差的时间复杂度和冒泡排序是一样的,为O(n2),平均时间复杂度为O(nlogn)。快速排序其实是基于“二分”思想。
1 #include <stdio.h> 2 3 int array[100], n; 4 5 void quicksort(int left, int right) 6 { 7 if (left > right) { 8 return; 9 } 10 int temp = array[left]; // 保存基准数 11 int i = left; // 哨兵i 12 int j = right; // 哨兵j 13 14 while (i != j) 15 { 16 // 哨兵j向左移动 17 while (array[j] >= temp && i < j) 18 j--; 19 // 哨兵i向右移动 20 while (array[i] <= temp && i < j) 21 i++; 22 // 交换两个哨兵脚下的数 23 if (i < j) 24 swap(array[i], array[j]); 25 } 26 27 // 将基准数归位 28 array[left] = array[i]; 29 array[i] = temp; 30 31 // 分别处理左右子序列 32 quicksort(left, i - 1); 33 quicksort(i + 1, right); 34 } 35 36 int main() 37 { 38 int n; 39 // 输入 40 scanf("%d", &n); 41 if (n > 100 || n <1) 42 return 0; 43 for (int i = 0; i < n; i++) 44 scanf("%d", &array[i]); 45 46 quicksort(0, n - 1); 47 // 输出 48 for (int i = 0; i< n; i++) 49 printf("%d", array[i]); 50 51 return 0; 52 }
相关知识
快速排序由 C. A. R. Hoare(Charles Antony Richard Hoare)在1960年提出,之后又有许多人做了进一步的优化。如果你对快速排序感兴趣可以去看看东尼霍尔1962年在Computer Journal发表的论文“Quicksort”以及《算法导论》的第七章。快速排序算法仅仅是东尼霍尔在计算机领域才能的第一次显露,后来他受到了老板的赏识和重用,公司希望他为新机器设计一个新的高级语言。要知道当时还没有PASCAL或者C语言这些高级的东东。后来东尼霍尔参加了由Edsger Wybe Dijkstra(1972年图灵奖得主)举办的“ALGOL 60”培训班,他觉得自己与其没有把握去设计一个新的语言,还不如对现有的“ALGOL 60”进行改进,使之能在公司的新机器上使用。于是他便设计了“ALGOL 60”的一个子集版本。这个版本在执行效率和可靠性上都在当时“ALGOL 60”的各种版本中首屈一指,因此东尼霍尔受到了国际学术界的重视。后来他在“ALGOL X”的设计中还发明了大家熟知的“case”语句,后来也被各种高级语言广泛采用,比如PASCAL、C、Java语言等等。当然,东尼霍尔在计算机领域的贡献还有很多很多,他在1980年获得了图灵奖。