Difficulty:medium
More:【目录】LeetCode Java实现
Description
Given an array nums containing n + 1 integers where each integer is between 1 and n(inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
Example 1:
Input: [1,3,4,2,2]
Output: 2
Example 2:
Input: [3,1,3,4,2] Output: 3
Note:
- You must not modify the array (assume the array is read only).
- You must use only constant, O(1) extra space.
- Your runtime complexity should be less than O(n2).
- There is only one duplicate number in the array, but it could be repeated more than once.
Intuition
we can regard the array as a linked list: treat the index as a node, treat the value as a next pointer. For example: (array =>linked List)

↓↓
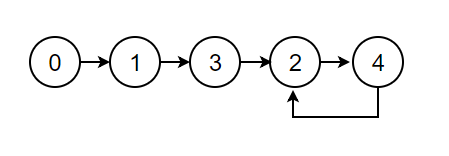
So we can transform this problem into a Linked List Cycle problem, refer to Linked List Cycle II for more details.
Solution
public int findDuplicate(int[] nums) {
if(nums==null)
return -1; //invalid
int fast=0;
int slow=0;
do{
fast=nums[nums[fast]];
slow=nums[slow];
}while(fast!=slow);
int entry=0;
while(entry!=slow){
entry=nums[entry];
slow=nums[slow];
}
return entry;
}
Complexity
Time complexity : O(n)
Space complexity : O(1)
What I've learned
there is a cycle in the list, becasue:
1. Two different indexes have the same value, which means two different nodes point to the same node.
2. node0 (index=0) will absolutely point to another node.
More:【目录】LeetCode Java实现