普通最小二乘法
理论:

损失函数:

权重计算:
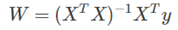
1、对于普通最小二乘的系数估计问题,其依赖于模型各项的相互独立性。
2、当各项是相关的,且设计矩阵 X的各列近似线性相关,那么,设计矩阵会趋向于奇异矩阵,这会导致最小二乘估计对于随机误差非常敏感,产生很大的方差。
例如,在没有实验设计的情况下收集到的数据,这种多重共线性(multicollinearity)的情况可能真的会出现。
使用:
from sklearn import datasets, linear_model
regr = linear_model.LinearRegression()
reg.fit(X_train, y_train)
岭回归
理论:
损失函数:
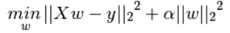
其中阿尔法大于0,它的值越大,收缩量越大,这样系数对公线性的鲁棒性也更强
当X矩阵不存在广义逆(即奇异性),最小二乘法将不再适用。可以使用岭回归
X矩阵不存在广义逆(即奇异性)的情况:
1)X本身存在线性相关关系(即多重共线性),即非满秩矩阵。
当采样值误差造成本身线性相关的样本矩阵仍然可以求出逆阵时,此时的逆阵非常不稳定,所求的解也没有什么意义。
2)当变量比样本多,即p>n时.
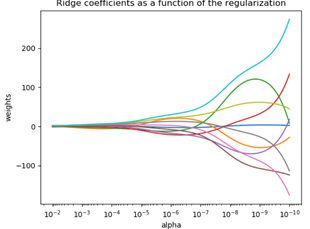
岭迹图:
岭迹图作用:
1)观察λ较佳取值;
2)观察变量是否有多重共线性;
在λ很小时,W很大,且不稳定,当λ增大到一定程度时,W系数迅速缩小,趋于稳定。
λ的选择:一般通过观察,选取喇叭口附近的值
岭参数的一般选择原则
选择λ值,使到
1)各回归系数的岭估计基本稳定;
2)用最小二乘估计时符号不合理的回归系数,其岭估计的符号变得合理;
3)回归系数没有不合乎实际意义的值;
4)残差平方和增大不太多。 一般λ越大,系数β会出现稳定的假象,但是残差平方和也会更大
岭回归选择变量的原则(仅供参考)
1)在岭回归中设计矩阵X已经中心化和标准化了,这样可以直接比较标准化岭回归系数的大小。可以剔除掉标准化岭回归系数比较稳定且值很小的自变量。
2)随着λ的增加,回归系数不稳定,震动趋于零的自变量也可以剔除。
3)如果依照上述去掉变量的原则,有若干个回归系数不稳定,究竟去掉几个,去掉哪几个,这无一般原则可循,这需根据去掉某个变量后重新进行岭回归分析的效果来确定。
使用:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
# #############################################################################
# Compute paths
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
coefs = []
for a in alphas:
ridge = linear_model.Ridge(alpha=a, fit_intercept=False)
ridge.fit(X, y)
coefs.append(ridge.coef_)
# #############################################################################
# Display results
ax = plt.gca()
ax.plot(alphas, coefs)
Lasso回归
理论:
维数灾难:
何谓高维数据?高维数据指数据的维度很高,甚至远大于样本量的个数。高维数据的明显的表现是:在空间中数据是非常稀疏的,与空间的维数相比样本量总是显得非常少。
在分析高维数据过程中碰到最大的问题就是维数的膨胀,也就是通常所说的“维数灾难”问题。研究表明,随着维数的增长,分析所需的空间样本数会呈指数增长。
如下所示,当数据空间维度由1增加为3,最明显的变化是其所需样本增加;换言之,当样本量确定时,样本密度将会降低,从而样本呈稀疏状态。假设样本量n=12,单个维度宽度为3,那在一维空间下,样本密度为12/3=4,在二维空间下,样本分布空间大小为3*3,则样本密度为12/9=1.33,在三维空间下样本密度为12/27=0.44。
设想一下,当数据空间为更高维时,X=[x1x1,x2x2,….,xnxn]会怎么样?
1、需要更多的样本,样本随着数据维度的增加呈指数型增长;
2、数据变得更稀疏,导致数据灾难;
3、在高维数据空间,预测将变得不再容易;
4、导致模型过拟合。
数据降维:
对于高维数据,维数灾难所带来的过拟合问题,其解决思路是:1)增加样本量;2)减少样本特征,而对于现实情况,会存在所能获取到的样本数据量有限的情况,甚至远小于数据维度,即:d>>n。如证券市场交易数据、多媒体图形图像视频数据、航天航空采集数据、生物特征数据等。
主成分分析作为一种数据降维方法,其出发点是通过整合原本的单一变量来得到一组新的综合变量,综合变量所代表的意义丰富且变量间互不相关,综合变量包含了原变量大部分的信息,这些综合变量称为主成分。主成分分析是在保留所有原变量的基础上,通过原变量的线性组合得到主成分,选取少数主成分就可保留原变量的绝大部分信息,这样就可用这几个主成分来代替原变量,从而达到降维的目的。
但是,主成分分析法只适用于数据空间维度小于样本量的情况,当数据空间维度很高时,将不再适用。
Lasso是另一种数据降维方法,该方法不仅适用于线性情况,也适用于非线性情况。Lasso是基于惩罚方法对样本数据进行变量选择,通过对原本的系数进行压缩,将原本很小的系数直接压缩至0,从而将这部分系数所对应的变量视为非显著性变量,将不显著的变量直接舍弃。
目标函数:
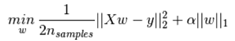
1、Lasso 是估计稀疏系数的线性模型。
2、它在一些情况下是有用的,因为它倾向于使用具有较少参数值的情况,有效地减少给定解决方案所依赖变量的数量。 因此,Lasso 及其变体是压缩感知领域的基础。 在一定条件下,它可以恢复一组非零权重的精确集
弹性网络
1、弹性网络 是一种使用 L1, L2 范数作为先验正则项训练的线性回归模型。
2、这种组合允许学习到一个只有少量参数是非零稀疏的模型,就像 Lasso 一样,但是它仍然保持 一些像 Ridge 的正则性质。我们可利用 l1_ratio 参数控制 L1 和 L2 的凸组合。
3、弹性网络在很多特征互相联系的情况下是非常有用的。Lasso 很可能只随机考虑这些特征中的一个,而弹性网络更倾向于选择两个。
4、在实践中,Lasso 和 Ridge 之间权衡的一个优势是它允许在循环过程(Under rotate)中继承 Ridge 的稳定性。
损失函数:

使用:
from sklearn.linear_model import ElasticNet
enet = ElasticNet(alpha=0.2, l1_ratio=0.7) #alpha=α l1_ratio=ρ