[论文简析]How Do Vision Transformers Work?[2202.06709]
-
论文题目:How Do Vision Transformers Work?
-
ICLR2022 - Reviewer Kvf7:
- 这个文章整理的太难懂了
- 很多trick很有用,但是作者并没有完全说明
-
行文线索 Emporocal Observations:
- MSAs(多头自注意力机制 / 一般取代CNN)能够提高CNN的预测性能,VIT里面能够很好的去预测 well-calibrated uncertainty P(模型输出的预测概率值)
- 鲁棒性,对于data corruptions、image occlusions、adversarial attacks、特别是对high-frequency noisy 高频噪声
- 靠近最后几层的MSAs能够显著的提高我们的性能
Q1:Inductive Biases 归纳偏置
-
归纳偏置可以理解为,从现实生活中观察到的现象中归纳出一定的规则(heuristics),然后对模型做一定的约束,从而可以起到“模型选择”的作用,即从假设空间中选择出更符合现实规则的模型。其实,贝叶斯学习中的“先验(Prior)”这个叫法,可能比“归纳偏置”更直观一些。
- CNN的inductive bias应该是locality和spatial invariance,即空间相近的grid elements有联系而远的没有,和空间不变性(kernel权重共享)
- RNN的inductive bias是sequentiality和time invariance,即序列顺序上的timesteps有联系,和时间变换的不变性(rnn权重共享)
-
MSA本质上是一个
generalized spatial smoothing广义空间平滑,由几个value在进行求和,权重由Q和K来给定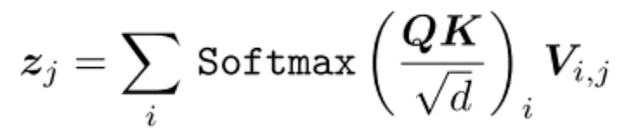
- 相对比于CNN和RNN而言,MSA的归纳偏置是
weak Inductive Biases,由于是全局soft-attention,因此会有长距离的关系long-range dependencies - 因此适当的约束
Appropriate constraints/ 强归纳偏置可能会对模型具有帮助:swin、twins(做局部attention)
Conclusion 1
- 因此
Conclusion 1:归纳偏置越强,预测/特征学出来的就越强。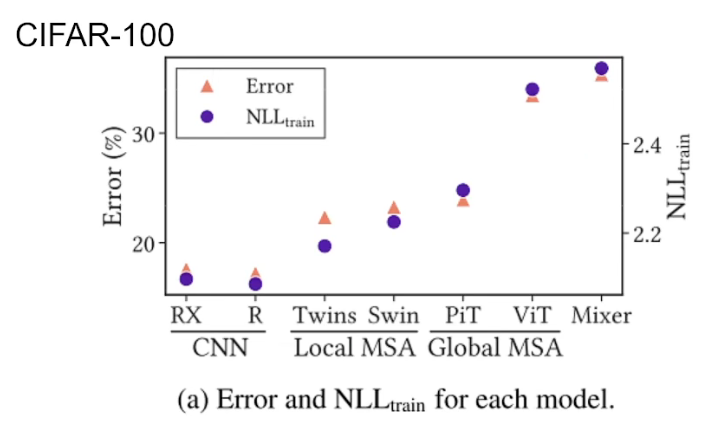
- RX:ResNeXt,R:ResNet,Mixes是最自由的
- 疑问1:会不会VIT这些模型在CIFAR-100小数据集上overfit过拟合才会导致性能差?- 实际上不是如此,可以看出随着训练集大小和训练时间长短变化,NLLtrain和Error仍然是相关,并没有出现过拟合现象。
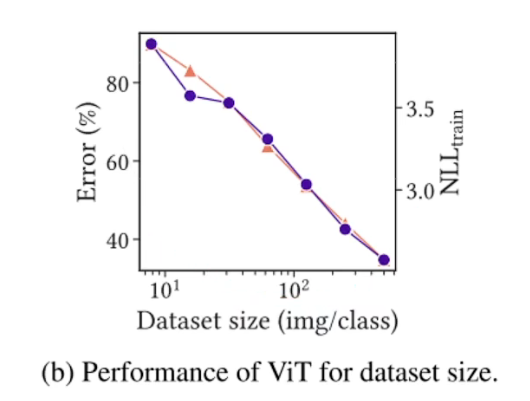
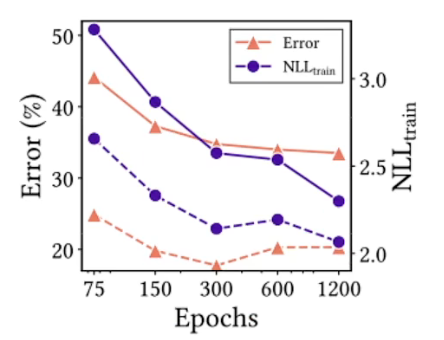
Conclusion 2
-
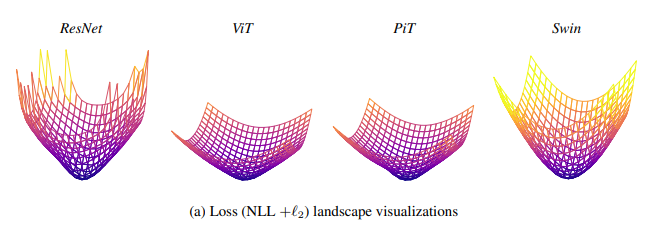
-
疑问2:能不能衡量convexity? - 统计很多个海塞矩阵的最大特征值,再用来做一个平谱来反映loss function的形状特性
Hessian Max Eigenvalue Spectrum(是这个作者的另一篇论文) -
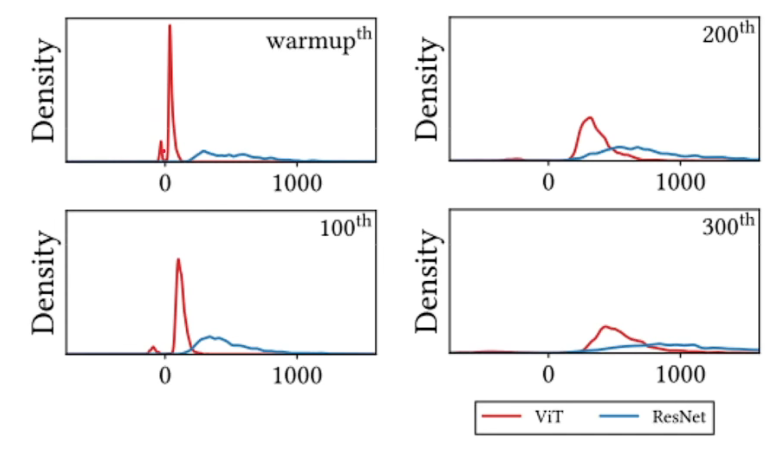
-
归纳偏置的作用:强的能够压制负的特征值
negative eigenvalues -
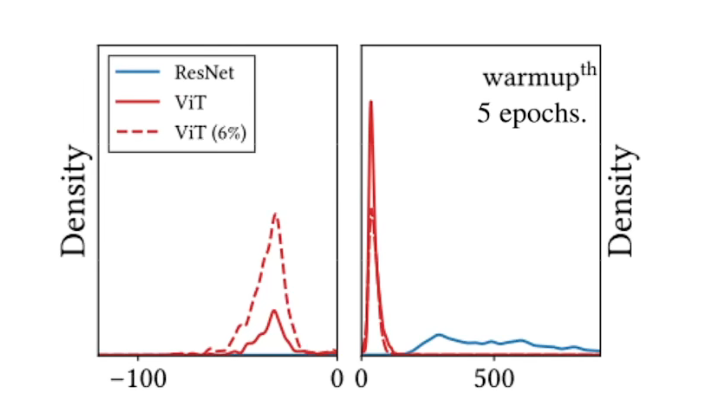
- VIT 6%表示少量数据集下,负特征值非常明显,随着样本数量增加,负特征值得到抑制
-
loss平滑是由MSA导致的,但是这并不一定是一个坏事:
regarding generalization & performance具有更好的表达能力,泛化可塑,随着样本数量的增加,可以去压制负特征值,让loss function变得没有那么平坦,让凸一些,与VIT适用于大数据量样本的观察是契合的。- ResNet更加陡峭,在大数据量样本下很容易陷入局部最优
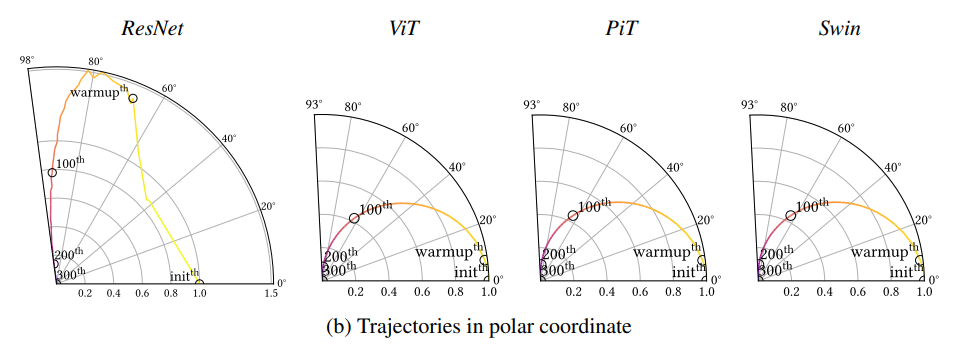
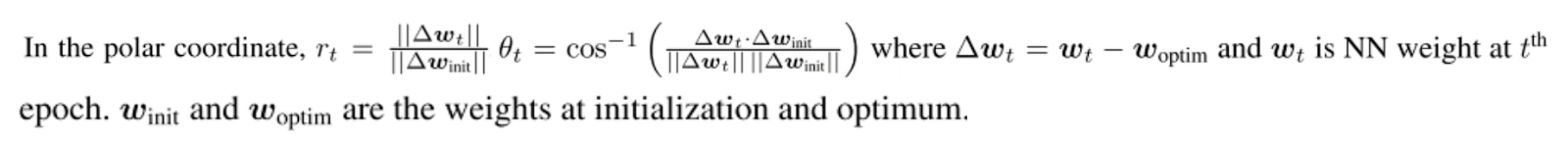
- 夹角越大说明离初始模型越来越不一样,
Transformer过度的十分平滑,越强的归纳偏置会导致优化的更加曲折,可以理解为执行力
-
以上就是说明,需要在归纳偏置和数据量之间寻找到一个平衡:
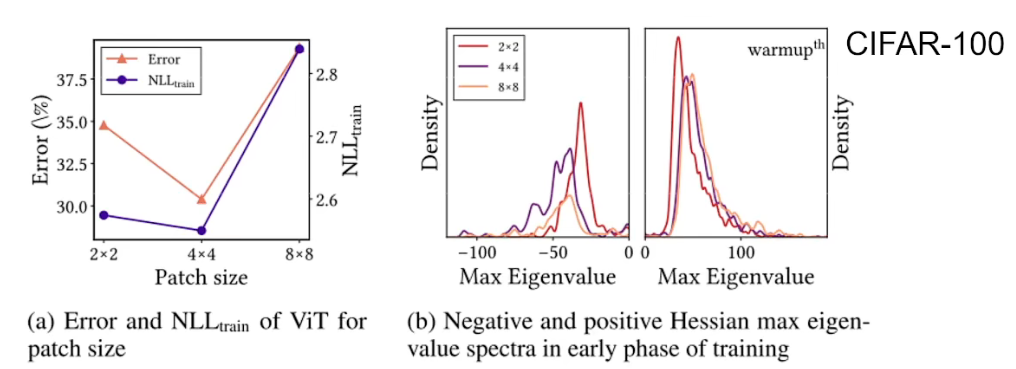
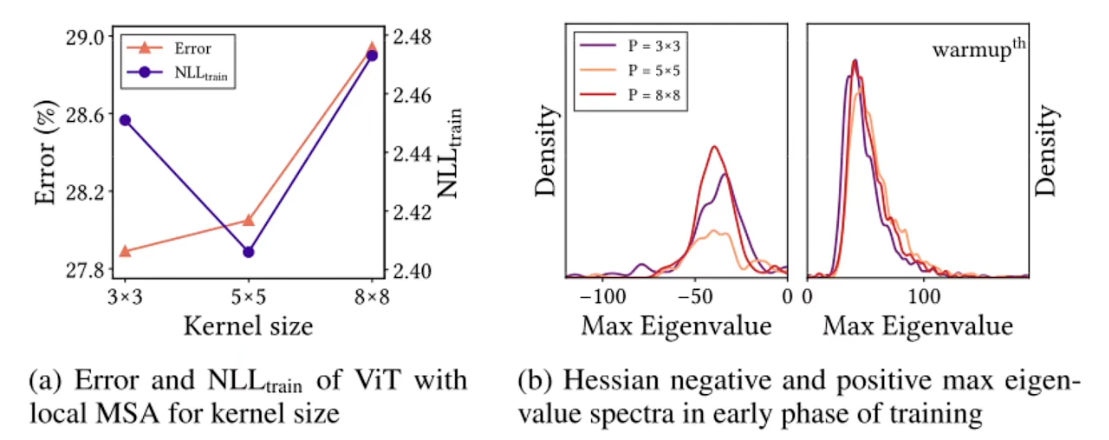
- patch_size ≈ CNN中的kernel大小,大小越大,偏执归纳越强,右图可以看出归纳偏置越强对负特征值的抑制越强(本质就是如何作用于loss function)
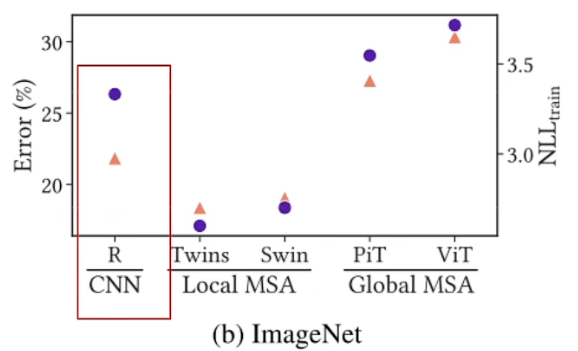
- 在ImageNet上,就是由于CNN其归纳偏置太强,导致没有MSA那么灵活,没有那么强的表达能力 / 泛化能力表达复杂的数据集。
-
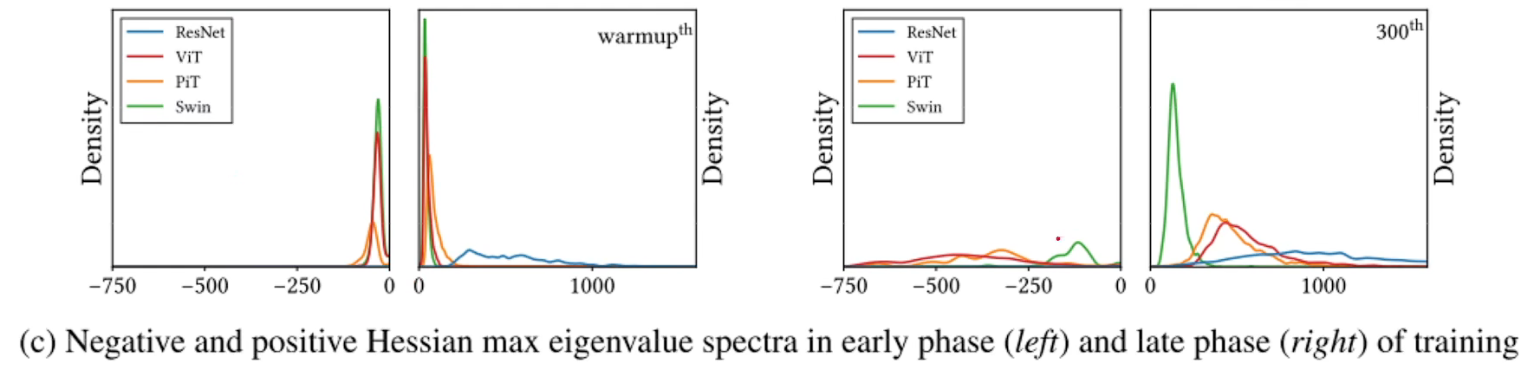
- local MSA / swin 滑窗机制产生了很多负特征值,但是它很大程度上减少了特征值的度量。有图看出swim相比其他的模型更加集中于靠近0的位置,说明swim的loss更加的平滑,甚至当训练过后也是。
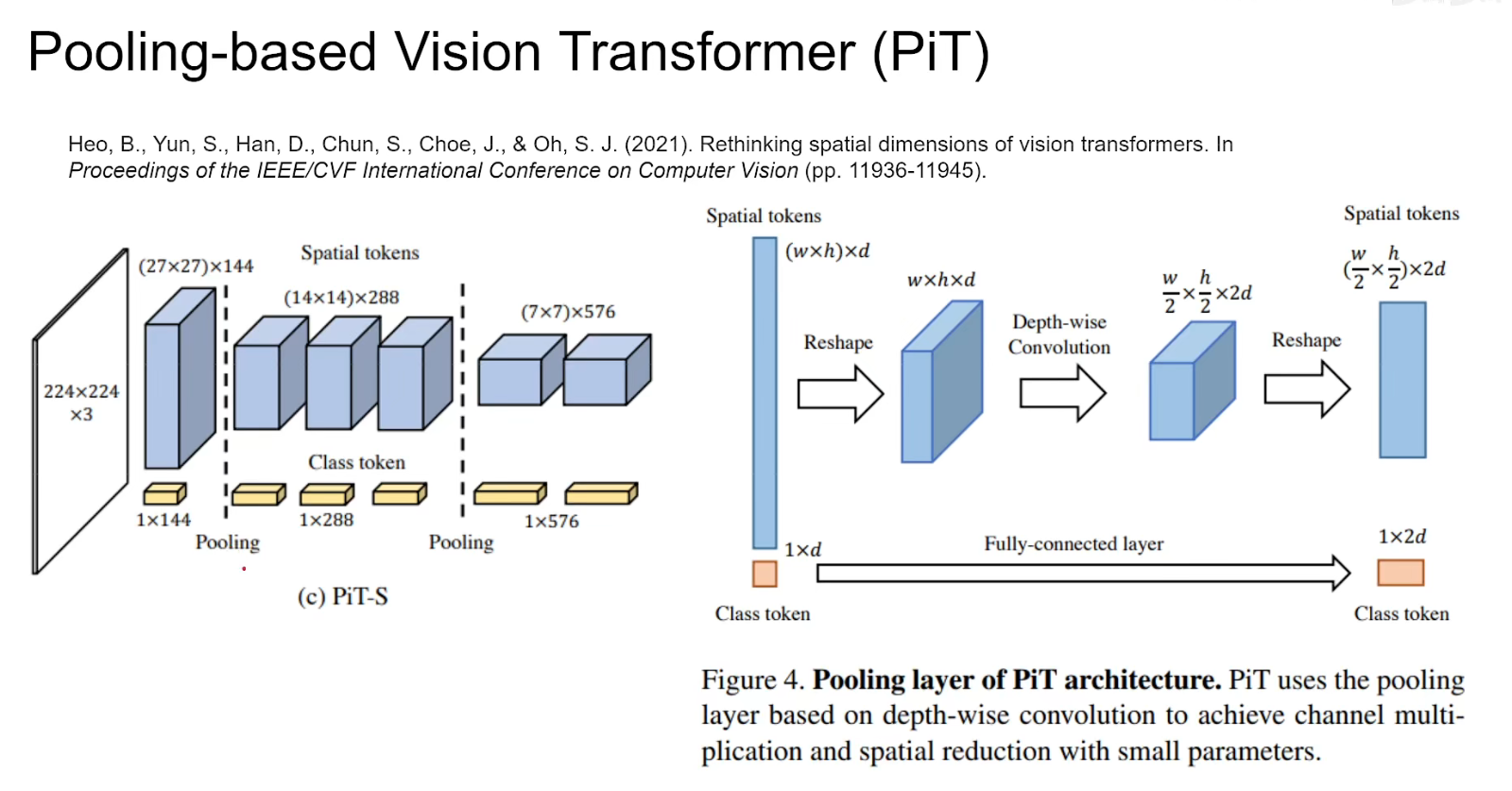
- PIT相对于VIT而言是一个
multi-stage多级的,不断的把模型shape缩小,深度增加,这种结构同样抑制了负的海塞矩阵特征值。 - 两种常用的设计如何影响特征值平谱。
-
除此之外:
- MSA中head的数量 = loss landspace convexity,head越多归纳偏置越强,因为每个head只跟自己交流。

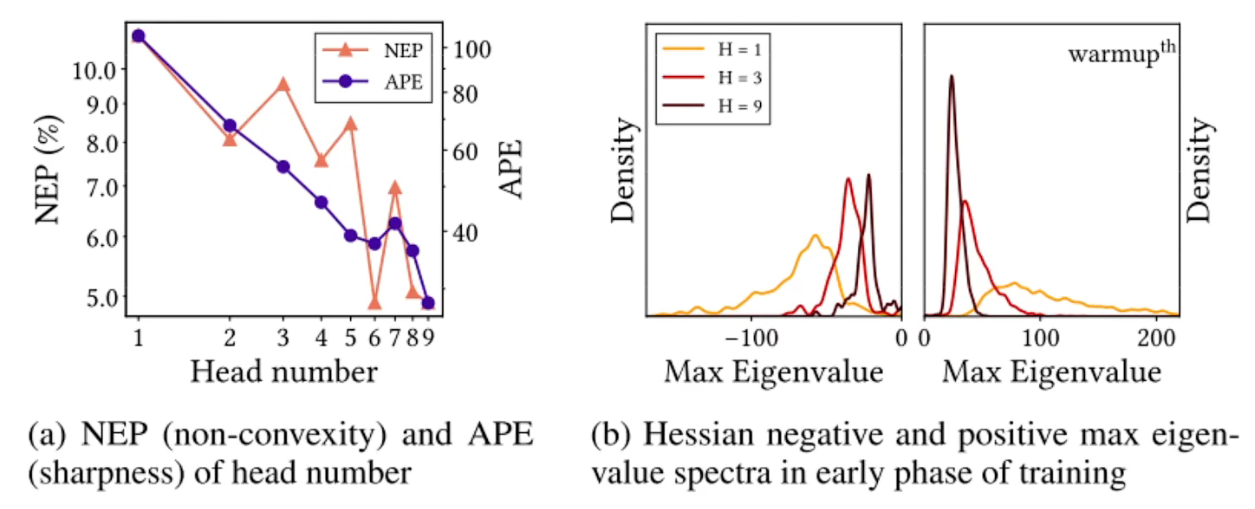
- NEP衡量负样本比例,APE衡量loss陡峭程度,随着head增加,都是下降的趋势,有图表示head越大,离0越近表示越来越平坦,面积越小表示越来越凸。
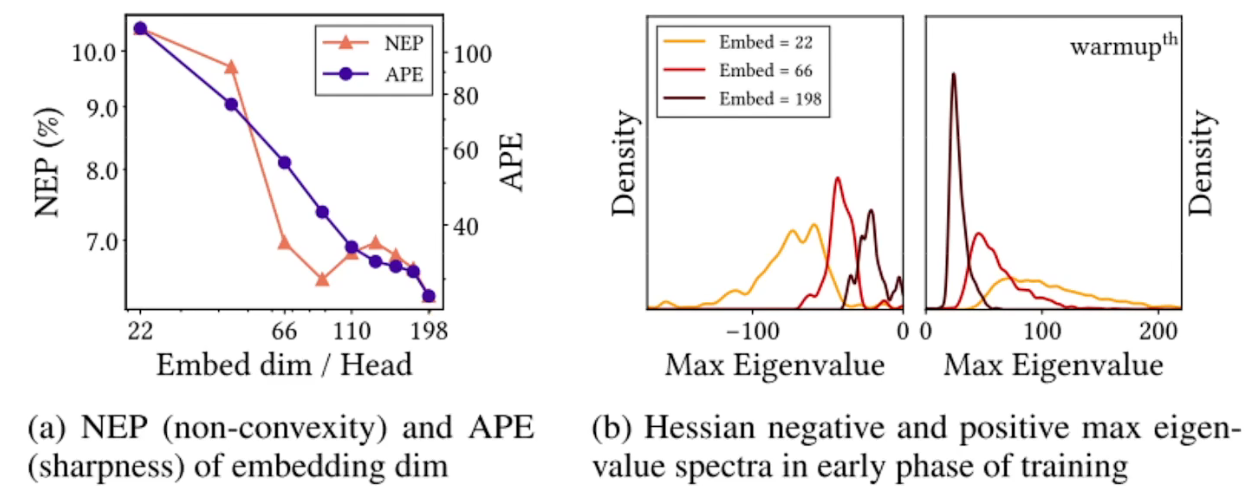
- 此图就是说明head的深度
Embed dim。
Conclusion 3
- loss landscape smoothing methods aisds 更平滑更凸
- 首先用GAP
Global Average Pooling而不用CLS 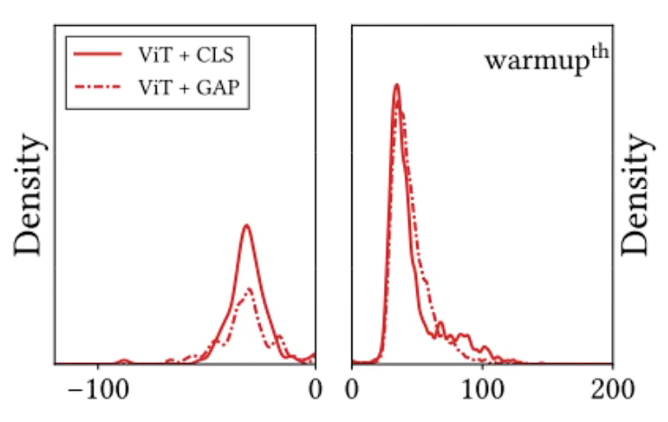
- SAM
Sharpness-Aware Minimization改善VIT的性能(另外两篇论文,一种梯度下降优化算法)
- 首先用GAP
总结
- 归纳偏置 <=> loss landscape convexity / smoothness & flatness <=> 海塞矩阵最大值norm
- MSA为什么让性能更好?
- 平坦 / loss不凸 / 数据量 / 平滑
另一个观察
- Data Specificity (not long-range dependency) 数据特异性(非全局关联)
- 实验:用NLP思想,将
global MSA替换2D conv MSA(1d局部,2d局部相邻head做attention) 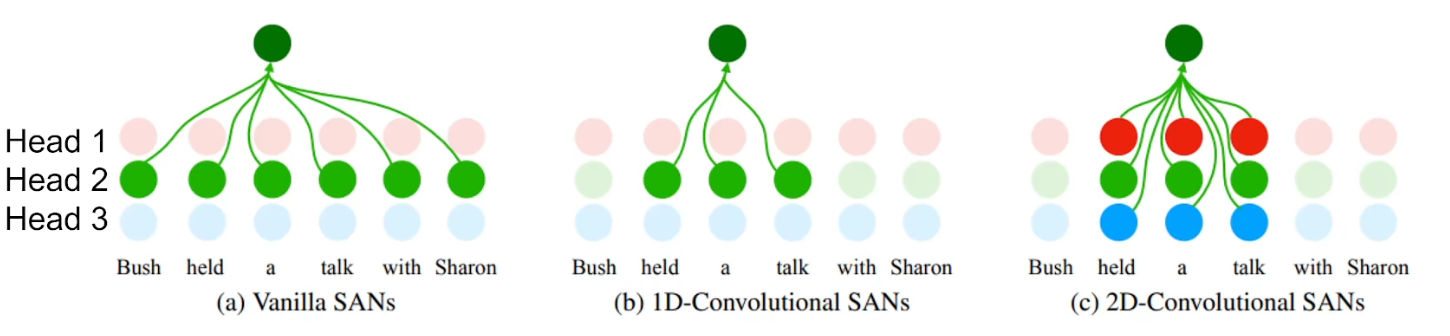
- 8X8kernel等效为全局attention,局部更加有利
- Data Specificity(attention)替代long-range dependency,用数据特异性来替代全局attention
- 实验:用NLP思想,将
Q2:MSAs和Convs差异
- Convs:data-agnostic and channel-specific 数据无关和通道特定,不管数据怎么样,权重都是固定好的,按照同样的权重去提取特征,特征放到特定的位置/channel
- MSA:data-specific and channel-agnostic 数据特定和通道无关,attention计算是和数据本身有关的,都是进来相乘做attention,进来顺序就不重要了。
- 可以看出这两者是相互的。
Conclusion 1
- MSA是低通滤波器(本质上就是把所有空间上的值求个平均),Conv是高通滤波器
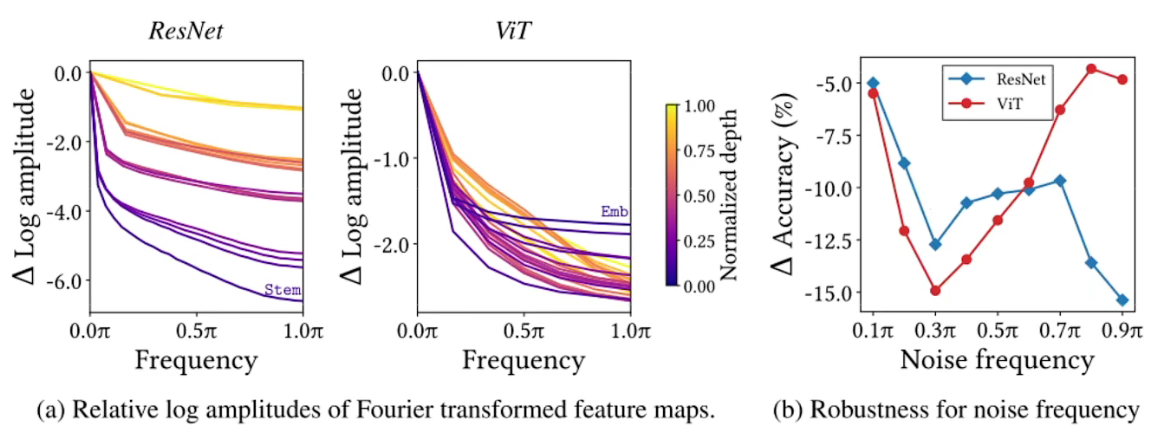
- 作者对两者输入不同频率得到输出后的可视化,可以看到,Convs对高频损失不大,低波段下降明显,而MSA相反。同样右图,对加入不同频率噪声的影响,Convs对高频噪声反应大,MAS对低频噪声反应大。
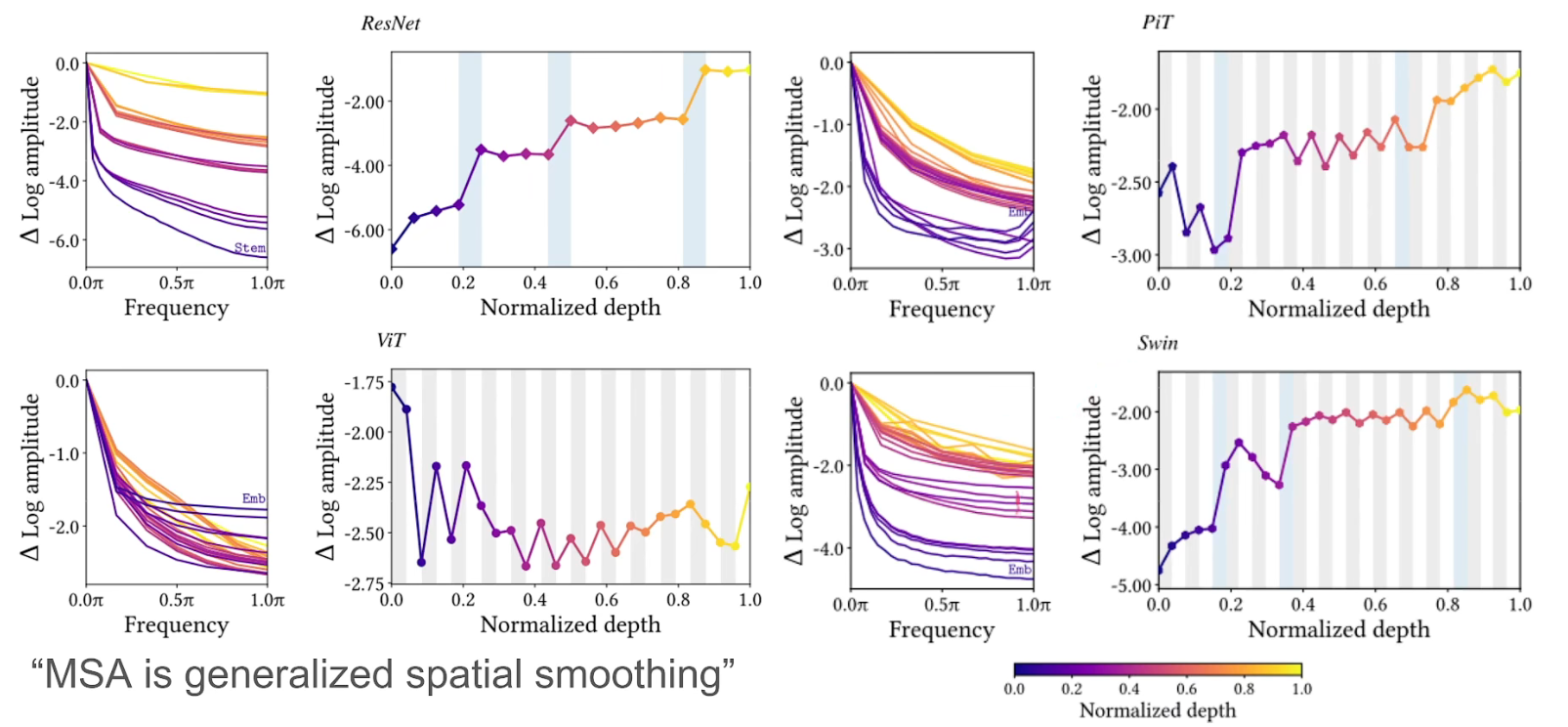
- 不过对于swim而言,它同样可以保持一定的高频信号。
- 看到可以看出,灰色部分的高层时可以减少高频信号的响应,而在白色部分都是增加高频信号的响应。低层的时候与高层相反。
Conclusion 2
- MSAs聚合特征,而Convs相反让特征更加多样。
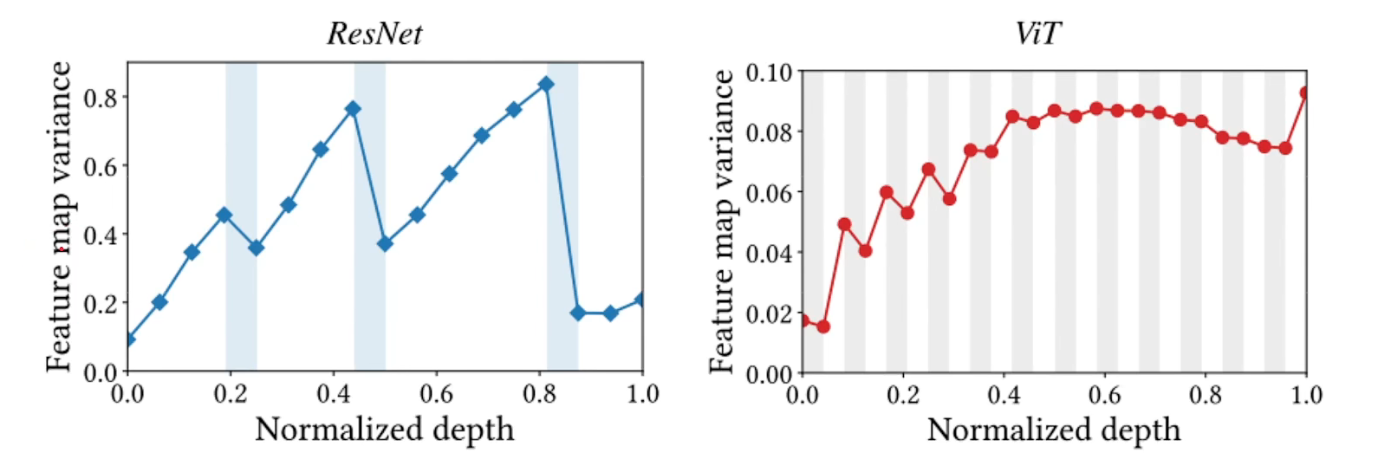
- 白色卷积/MLP多层感知机部分提高方差,蓝色部分下采样降低方差。
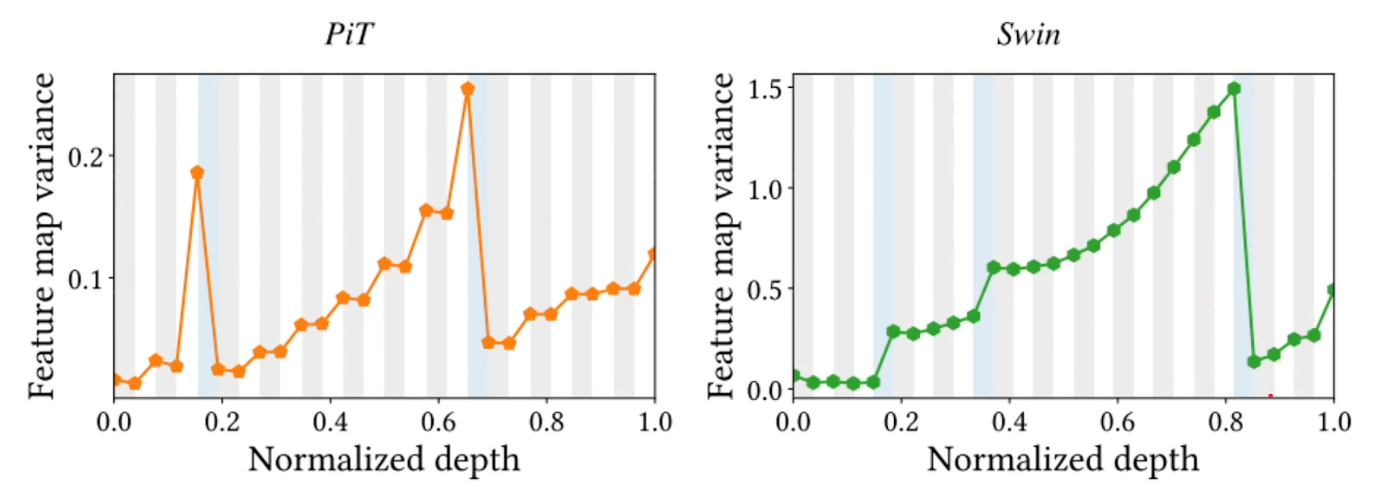
- 有意思的是在swim中,表现得更像是一个Convs的结构,方差逐渐的增加,甚至在做下采样的时候方差还在增加,直到最后的时候方差才降下来,不知道如何解释。
- 总的来说这意味着就是,我们或许可以将两者的性质结合起来设计一个更好的网络。
Q3:结合MSA+Conv
-
-
可以看出来,在Resnet/PIT/Swin中是多层结构,(小块)层之内相关性明显,层之间相关性很弱 / PIT也是一样。而在VIT里面,由于本身就没有Multi-stage的概念,所以一大块都是相关的。
-
这个图使用:Minibatch Centered Kernel Alignment(CKA)计算出来的。
-
-
从已经训练好的Res和Swin里面移除网络单元进行测试性能
-
对于ResNet而言,移除早期的模块比后期的模块更重要,同一层中移除前面的比移除后面的更致命。
-
对于Swin而言,在stage(以蓝色下采样为划分)中,开头移除MLP会大幅影响准确性,结尾移除MSA会大幅影响准确性。
-
基于以上观察,把Convs逐渐替换成Attention有三个准则:
- 1、从全局最后开始,每隔一层把Conv块替换成MSA块
- 2、如果替换的MSA并不能增加我们模型的性能,那么我们去找到上一个stage,在该stage的最后把Conv替换成MSA(同时不能增加性能的MSA还原成Conv)
- 3、在相对比较靠后的stage里,我们的MSA需要有更多的head以及更大的
hidden dimensions - 1、Alternately replace Conv blocks with MSA blocks from the end.
- 2、lf the added MSA block does not improve predictive performance, replace a Conv block located at the end of an earlier stage with an MSA block .
- 3、Use more heads and higher hidden dimensions for MSA blocks in late stages.
-
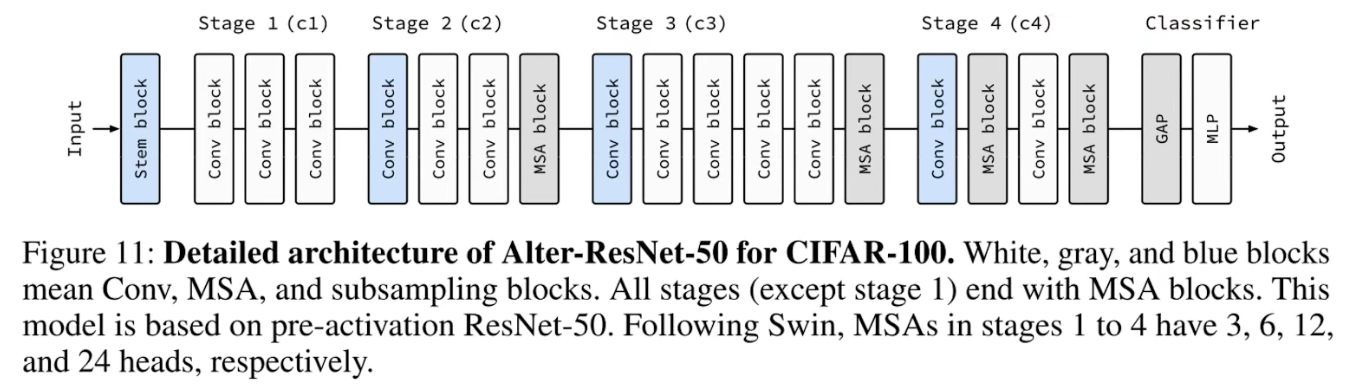
-
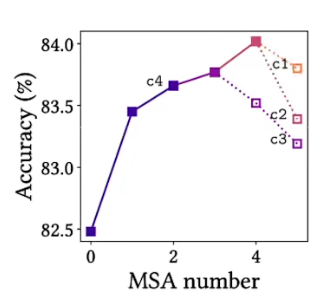
-
-
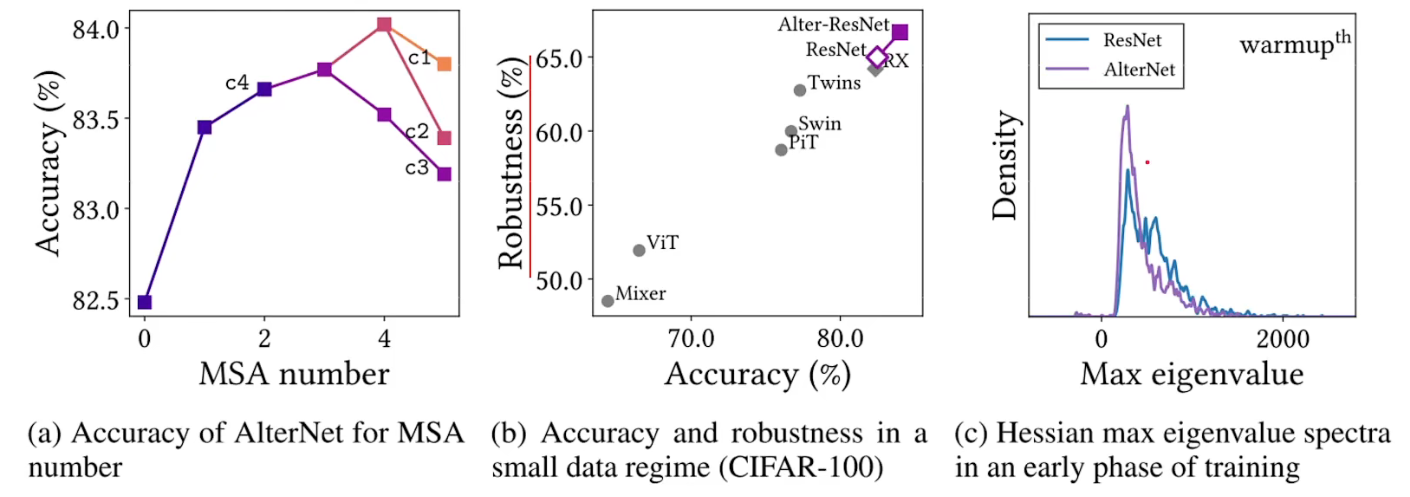
可以看到替换后的结果:精度有提升,鲁棒性有提升,eigenvalue频谱可以看出AlterNet更加平滑(特征值更加接近0)。鲁棒性计算另一篇论文。
-
-
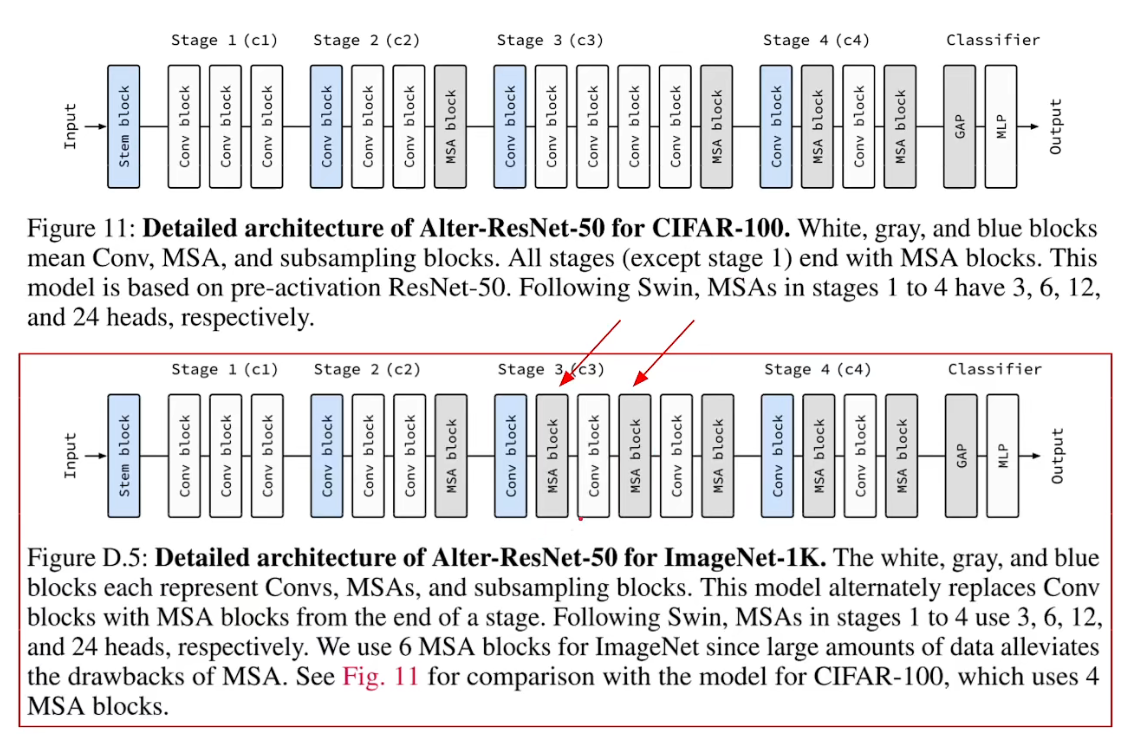
不同数据集针对的修改网络不一样,ImageNet相比于CIFAR上多了两个MSA层,这意味着我们有更弱的归纳偏置,更加强的表达性能,更多的数据才能支撑起更多的MSA。
-
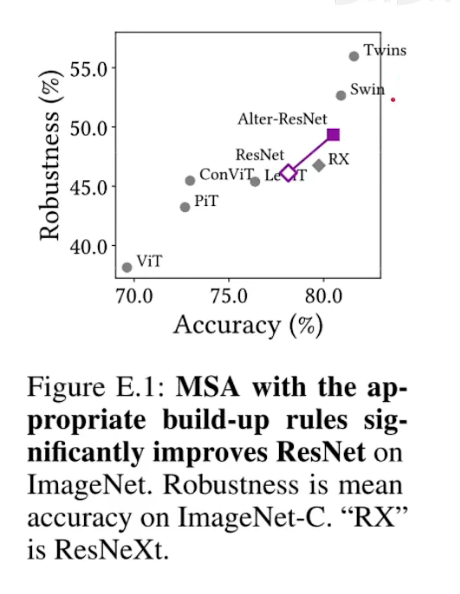
-
我们可以看到,相比于swin/ twins这种纯MSA的网络而言,在大数据集下性能肯定是不如的,因为他们的归纳偏置更加的弱。
一个发现
data augmention数据增强- 1、
Data augmentation can harm uncertainty calibration数据增强会损害不确定性校准 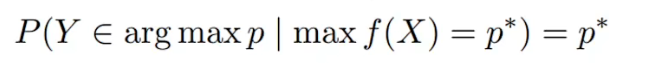
- 在没有进行数据增强前,模型对自己的预测比较自信,在进行数据增强后,模型对自己的预测反而不太自信了。
- 2、
Data augmentation reduces the magnitude of Hessian eigenvalues数据增强降低了 Hessian 特征值的大小 - 可以看出加了数据增强后的特征值更加趋向于0了,即表明loss变得更加平滑了,负的特征值变多了表示loss函数不凸了。
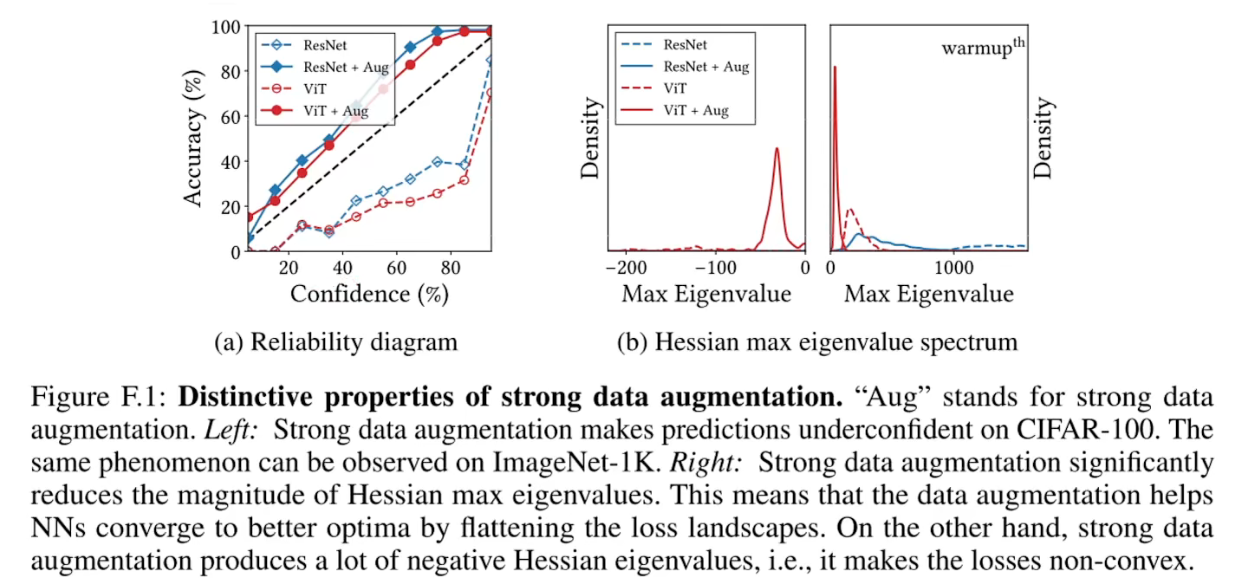
- 1、
总结
-

-
附录B:
- MSA is Spatial smoothing: Appendix B
Taking all these observations together, we provide an explanation of how MSAs work by addressing themselves as a general form of spatial smoothing or an implementation of data-complemented BNN. Spatial smoothing improves performance in the following ways:
1、Spatial smoothing helps in NN optimization by flattening the loss landscapes. Even a small 2×2 box blurfilter significantly improves performance.
2、Spatial smoothing is a low-pass filter. CNNs are vulnerable to high-frequency noises, but spatial smoothing improves the robustness against suchnoises by significantly reducing these noises.
3、Spatial smoothing is effective when applied atthe end of a stage because it aggregates all transformed feature maps. This paper shows that these mechanisms also apply to MSAs.
- MSA is Spatial smoothing: Appendix B