思路:
如果直接去连边然后跑最小生成树的话,不难发现边数是(O(nq))级别的。
于是我们可以观察一下这一张图:
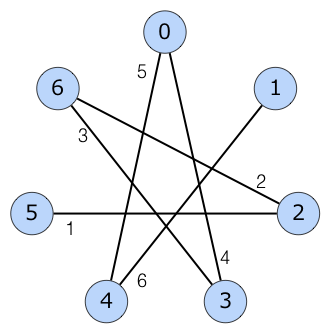
不难发现每次添加的边是相邻的两个点之间互相连边,并且很重要的是,边权一次一次地变大。
考虑Kruskal的过程,如果有两条边((u_1,v_1,w_1),(u_2,v_2,w_2)),并且(w_1<w_2),那么可以肯定的是,在考虑第二条边的时候,第一条边的两个点一定已经在一个连通块里面了。
再考虑一下Prim的过程,不难发现对于一个未加入当前连通块的点,我们关心的只是这个点离连通块的最小距离,这个时候它自己本身与哪个点相连已经不重要了。
于是整个算法的大致思路已经出来了,对于一组连续的边((a,b,w_1),(b,c,w_2),w_1<w_2),由于a,b之前一定在一个连通块内,所以第二条边可以改为((a,c,w_2))。
不难发现这样重新连边之后所有的边都是这样的形式((a,a+1,w)),于是我们开一个数组记录下来,之后再递推一遍便可以得到环上的那(O(n))条边了。之后再做一遍Kruskal即可。
#include<bits/stdc++.h>
#define REP(i,a,b) for(int i=a,i##_end_=b;i<=i##_end_;++i)
#define DREP(i,a,b) for(int i=a,i##_end_=b;i>=i##_end_;--i)
#define debug(x) cout<<#x<<"="<<x<<endl
#define fi first
#define se second
#define mk make_pair
#define pb push_back
typedef long long ll;
using namespace std;
void File(){
freopen("gkk.in","r",stdin);
freopen("gkk.out","w",stdout);
}
template<typename T>void read(T &_){
T __=0,mul=1; char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')mul=-1;
ch=getchar();
}
while(isdigit(ch))__=(__<<1)+(__<<3)+(ch^'0'),ch=getchar();
_=__*mul;
}
const int maxn=2e5+10;
const int maxm=1e6+10;
int n,q,m;
ll f[maxn];
struct edge{
int u,v;
ll w;
bool operator < (const edge & ano) const {
return w<ano.w;
}
}E[maxm];
namespace Kruskal{
ll ans;
int fa[maxn];
int find(int x){return fa[x]==x ? x : fa[x]=find(fa[x]);}
void work(){
REP(i,0,n-1)fa[i]=i;
sort(E+1,E+m+1);
REP(i,1,m){
int u=E[i].u,v=E[i].v;
if(find(u)==find(v))continue;
fa[find(u)]=find(v);
ans+=E[i].w;
}
printf("%lld
",ans);
}
}
int main(){
File();
read(n); read(q);
memset(f,63,sizeof(f));
int u,v; ll w;
REP(i,1,q){
read(u),read(v),read(w);
E[++m]=(edge){u,v,w};
f[u]=min(f[u],w+1);
f[v]=min(f[v],w+2);
}
REP(i,0,2*n-1){
int pre= !(i%n) ? n-1 : i%n-1;
f[i%n]=min(f[i%n],f[pre]+2);
}
REP(i,0,n-1){
int nex=(i+1)%n;
E[++m]=(edge){i,nex,f[i]};
}
Kruskal::work();
return 0;
}