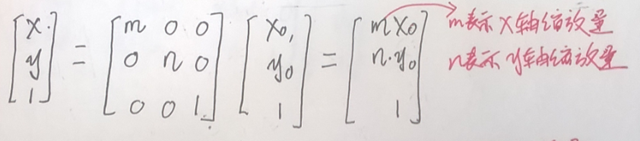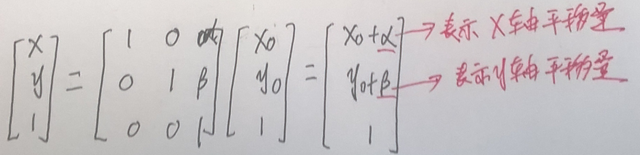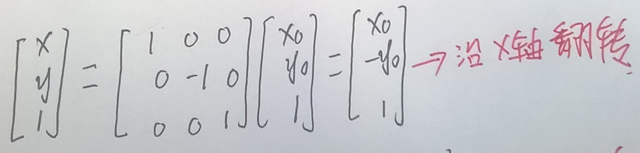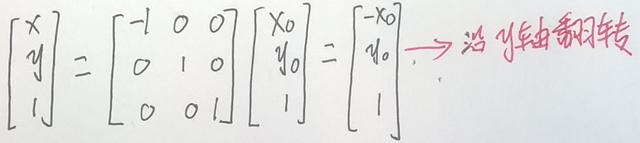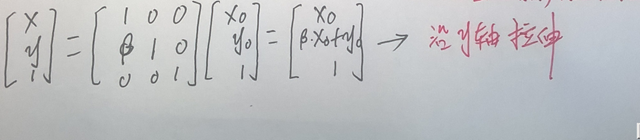什么是二维仿射呢变换呢?这么说的哈:在变换过程中,它保持了二维图形的“平直性”(即:直线经过变换之后依然是直线)和“平行性”(即:二维图形之间的相对位置关系保持不变,平行线依然是平行线,且直线上点的位置顺序不变)。如,旋转、平移、缩放、错切。我们来一个一个地看。
为了能实现平移操作,我们现在规定,我们都是在我们的二维坐标基础上再补充一个1,即由[x, y]T变为[x, y, 1]T.
缩放操作:
坐标由[x, y,1]T 变为[mx, ny, 1]T。用矩阵表示为:
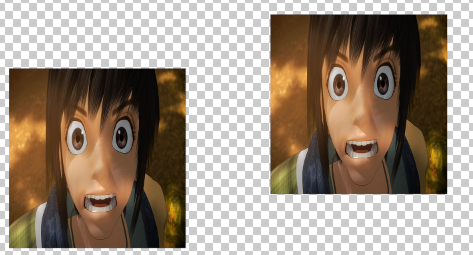
例子如下图所示:
平移操作:
用矩阵可以表示为:
例子如下图所示:
翻转操作:
可以分为沿x轴翻转和沿y 轴翻转,
当沿x轴翻转时,又称为垂直翻转,可以表示为:
例子如:
当沿y轴翻转时,又称为翻转,可以表示为:
例子如下:
错切操作:
同样,它可以分为沿x轴与沿y轴两种(当然你也可以把它们组合起来)
沿x 轴的错切操作,可以用矩阵表示为:
例子如下:
沿y 轴的错切操作,可以用矩阵表示为:
例子如下:
旋转操作:
我们先来推导一下以原点为中心的旋转操作。对于不以原点为旋转操作与以原点为中心的旋转操作的区别在于有一个平移操作啦,我们可以旋转完以后再平移,也可以平移完以后再旋转中啦。
它的例子如下:
好啦,基本的仿射变换就这么多啦,另外,别忘了我们可以通过把这些基本的变换组合起来实现更复杂的仿射变换。