线性回归模型的评估指标

在回归任务（对连续值的预测）中，常见的评估指标（Metric）有：平均绝对误差（Mean Absolute Error,MAE）、均方误差（Mean Square Error,MSE）、均方根误差（Root Mean Square Error,RMSE）和平均绝对百分比误差（Mean Absolute Percentage Error,MAPE），其中用得最为广泛的就是MAE和MSE。下面依次来进行一个大致的介绍，同时对于下面所有的计算公式：均表示样本数量、均表示第个样本的真实值、均表示第个样本的预测值。

一、评价回归模型的指标

1，均方误差

均方误差（MSE）的定义如下，即线性回归的损失函数，

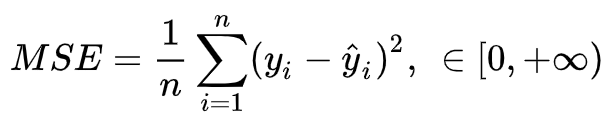
2，均方根误差

均方根误差（RMSE）是回归模型的典型指标，用于指示模型在预测中会产生多大的误差，对于较大的误差，权重较高。

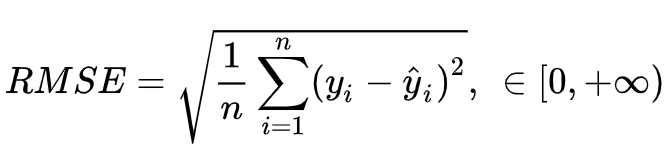
 y是实际值，而是预测值， RMSE越小越好。

3，平均绝对误差
平均绝对误差（MAE）用来衡量预测值与真实值之间的平均绝对误差，MAE越小表示模型越好，其定义如下：

4，R2分数

sklearn在实现线性回归时默认采用了[公式]指标，[公式]越大表示模型越好，其定义如下：

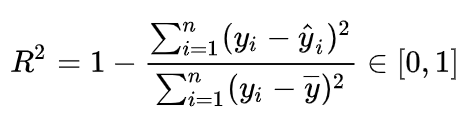
 其中表示真实值的平均值。可能的好处在于其结果进行了归一化，更容易看出模型间的差距。

二、偏差和方差

偏差：描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据。

方差：描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散。

三、sklearn的代码示例

import numpy as np
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression

def MAE(y, y_pre):
    return np.mean(np.abs(y - y_pre))
def MSE(y, y_pre):
    return np.mean((y - y_pre) ** 2)
def RMSE(y, y_pre):
    return np.sqrt(MSE(y, y_pre))
def MAPE(y, y_pre):
    return np.mean(np.abs((y - y_pre) / y))
def R2(y, y_pre):
    u = np.sum((y - y_pre) ** 2)
    v = np.sum((y - np.mean(y)) ** 2)
    return 1 - (u / v)

def load_data():
    data = load_boston()
    print(data)
    x = data.data
    y = data.target
    return x, y

def train(x, y):
    model = LinearRegression()
    model.fit(x, y)
    y_pre = model.predict(x)
    print("model score: ", model.score(x, y))
    print("MAE: ", MAE(y, y_pre))
    print("MSE: ", MSE(y, y_pre))
    print("MAPE: ", MAPE(y, y_pre))
    print("R^2: ", R2(y, y_pre))

if __name__ == '__main__':
    x, y = load_data()
    train(x, y)

参考：1.评估回归模型的指标：MSE、RMSE、MAE、R2、偏差和方差

　　　2.线性回归（模型的评估)