EM算法也称期望最大化（Expectation-Maximum,简称EM）算法，它是一个基础算法，是很多机器学习领域算法的基础，比如隐式马尔科夫算法（HMM）， LDA主题模型的变分推断，混合高斯模型GMM，基于概率统计的pLSA模型。
EM算法概述(原文)
我们经常会从样本观察数据中，找出样本的模型参数。 最常用的方法就是极大化模型分布的对数似然函数。
但是在一些情况下，我们得到的观察数据有未观察到的隐含数据，此时我们未知的有隐含数据和模型参数，因而无法直接用极大化对数似然函数得到模型分布的参数。这时可以使用EM算法。
EM算法解决这个的思路是使用启发式的迭代方法，既然我们无法直接求出模型分布参数，那么我们可以先猜想隐含数据（EM算法的E步），接着基于观察数据和猜测的隐含数据一起来极大化对数似然，求解我们的模型参数（EM算法的M步)。由于我们之前的隐藏数据是猜测的，所以此时得到的模型参数一般还不是我们想要的结果。不过没关系，我们基于当前得到的模型参数，继续猜测隐含数据（EM算法的E步），然后继续极大化对数似然，求解我们的模型参数（EM算法的M步)。以此类推，不断的迭代下去，直到模型分布参数基本无变化，算法收敛，找到合适的模型参数。
从上面的描述可以看出，EM算法是迭代求解最大值的算法，同时算法在每一次迭代时分为两步，E步和M步。一轮轮迭代更新隐含数据和模型分布参数，直到收敛，即得到我们需要的模型参数。
一个最直观了解EM算法思路的是K-Means算法。在K-Means聚类时，每个聚类簇的质心是隐含数据。我们会假设K个初始化质心，即EM算法的E步；然后计算得到每个样本最近的质心，并把样本聚类到最近的这个质心，即EM算法的M步。重复这个E步和M步，直到质心不再变化为止，这样就完成了K-Means聚类。
当然，K-Means算法是比较简单的，实际中的问题往往没有这么简单。上面对EM算法的描述还很粗糙，我们需要用数学的语言精准描述。
EM算法的推导
对于m个样本观察数据x=(x(1),x(2),...x(m))中，找出样本的模型p(x,z)参数θ, 对数似然函数如下：
模型中存在隐函数z=(z(1),z(2),...z(m))随机变量，不方便直接找到参数估计，所以这时候引入Q(Z(i)),注意不是随便引入一个函数的，这个函数是Z的一个分布，且Q(Z(i))≥0，这时为了让原来的对数似然函数不变，我们可以作出如下（2）变换公式：
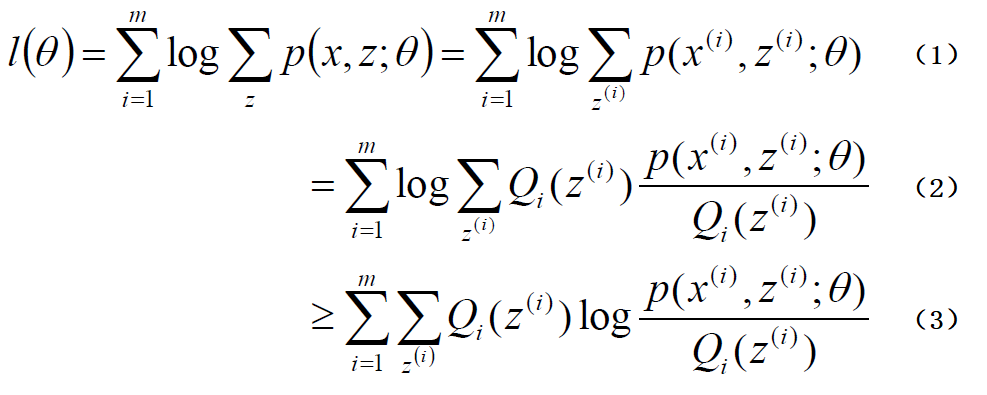
第（3）步利用了Jensen不等式。
Jensen不等式：若f是凸函数：
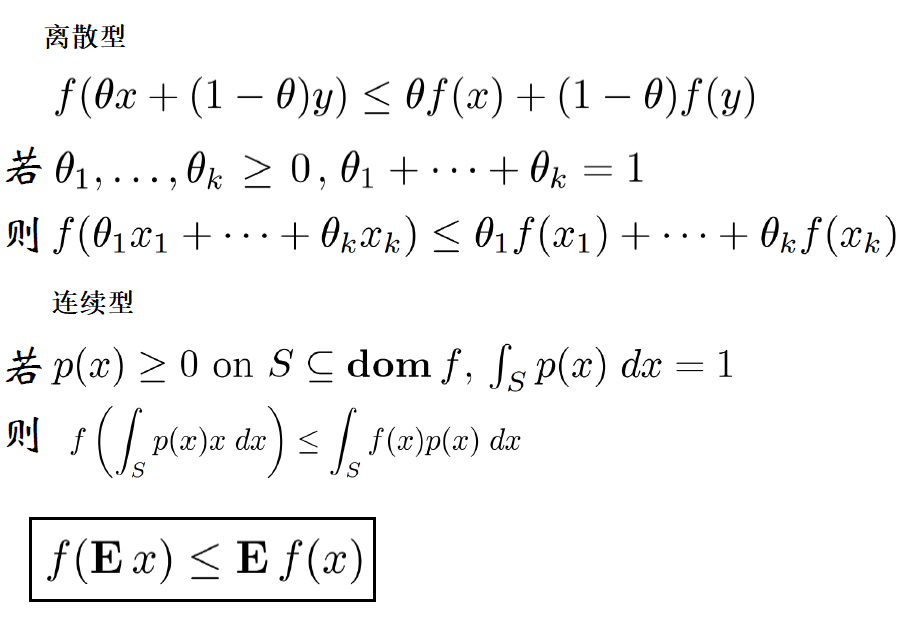
对于第（3）步中不等式中，若要满足相等的情况，需要满足条件：
c为常数，又因为：
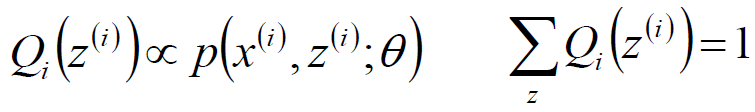
所以可以推出：
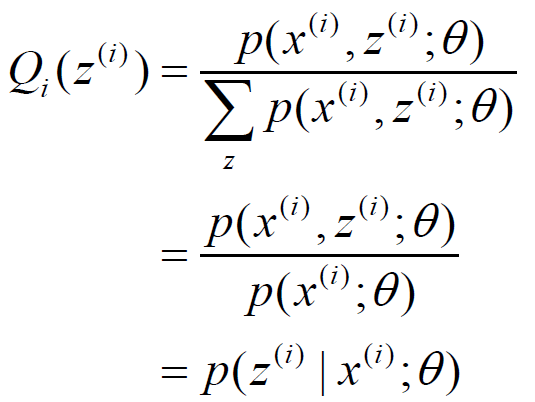
如果Qi(z(i))=P(z(i)|x(i);θ)), 则第(3)式是我们的包含隐藏数据的对数似然的一个下界。如果我们能极大化这个下界，则也在尝试极大化我们的对数似然。即我们需要最大化下式：
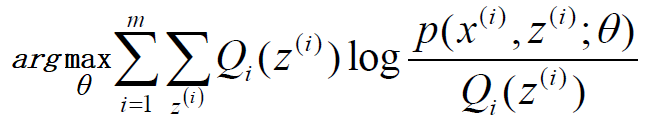
去掉上式中为常数的部分，则我们需要极大化的对数似然下界为：
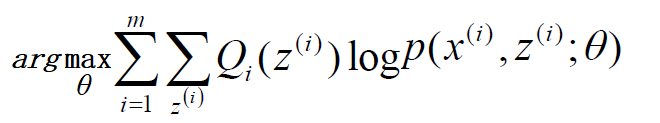
上式也就是我们的EM算法的M步，那E步呢？注意到上式中Qi(z(i))是一个分布，因此
可以理解为logP(x(i),z(i);θ)基于条件概率分布Qi(z(i))的期望。
EM算法的流程总结：
输入：观察数据x=(x(1),x(2),...x(m))，联合分布p(x,z;θ), 条件分布p(z|x;θ), 最大迭代次数J。
1) 随机初始化模型参数θ的初值θ0。
2） for j from 1 to J开始EM算法迭代：
a) E步：计算联合分布的条件概率期望：
Qi(z(i))=P(z(i)|x(i),θj)
b) M步：极大化L(θ,θj),得到θj+1:
c) 如果θj+1已收敛，则算法结束。否则继续回到步骤a)进行E步迭代。
输出：模型参数θ。
关于EM算法的收敛性可以参照此博文的EM算法的收敛性思考。
补充：
如果我们从算法思想的角度来思考EM算法，我们可以发现我们的算法里已知的是观察数据，未知的是隐含数据和模型参数，在E步，我们所做的事情是固定模型参数的值，优化隐含数据的分布，而在M步，我们所做的事情是固定隐含数据分布，优化模型参数的值。