java 递归及其经典应用--求阶乘、打印文件信息、计算斐波那契数列

什么是递归

我先看下百度百科的解释：
一种计算过程，如果其中每一步都要用到前一步或前几步的结果，称为递归的。用递归过程定义的函数，称为递归函数，例如连加、连乘及阶乘等。凡是递归的函数，都是可计算的，即能行的 。
古典递归函数，是一种定义在自然数集合上的函数，它的未知值往往要通过有限次运算回归到已知值来求出，故称为“递归”。它是古典递归函数论的研究对象 。

简单的说，递归一定要有递归体头和递归体。

递归头：什么时候不调用自己方法，即递归的结束条件
递归体：什么时候需要调用自己方法，即自己调用自己

如果一个方法没有递归头jvm在运行方法时，就会不断开辟栈幁(Stack Frame) 造成栈溢出，抛出 java.lang.StackOverflowError 异常。
我们看下面代码：

package com.xzlf.recursion;

public class Test {
	public static void main(String[] args) {
		a();
	}
	
	public static void a() {
		System.out.println("Test.a()");
		a();
	}

}

显然在a() 方法中没有终止调用a() 方法的条件，那么就会一直调用下去，直到吧栈内存用完。所以以上代码运行时，会一种执行打印语句，然后在栈溢出是抛出异常。
下面是代码运行结果：

如果我们加上一个终止条件就不会有无限调用情况了：

package com.xzlf.recursion;

public class Test {
	public static int num = 10;
	public static void main(String[] args) {
		a();
	}
	
	public static void a() {
		num--;
		System.out.println("Test.a() " + num);
		if(num > 0) {
			a();
		}
	}

}

修改后程序运行结果：

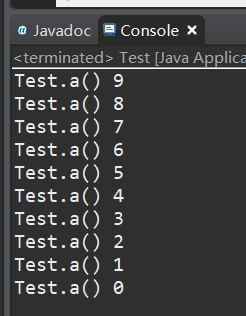
好了程序在不满足条件时，终止调用，我们的递归完成了。

递归应用

求阶乘

其实阶乘我们用普通for循环后while循环也能实现

/**
	 * 普通while循环球阶乘
	 * @param n
	 * @return
	 */
	public static long factorialForWhile(int n) {
		long result = 1;
		while(n > 1) {
			result *= n ; 
			n --;
		}
		return result;
	}

使用递归写法：

/**
	 * 递归算法球阶乘
	 * @param n
	 * @return
	 */
	
	public static long factorial(int n) {
		// 递归头
		if(n == 1) { 
			return 1;
		}
		// 递归体
		return n * factorial(n-1);// n! = n * (n - 1)
	}

测试以上代码：

public static void main(String[] args) {
		int n = 10;
		long r1 = factorial(n);
		long r2 = factorialForWhile(n);
		System.out.println("递归算法结果：" + r1);
		System.out.println("while循环结果：" + r2);
	}

以上运行结果为：

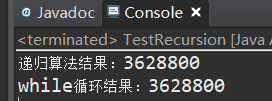
可以看到两种写法得到的结果一样。

打印文件信息

我们来打印tomcat/webapp下面一个mananger目录下文件信息，并使用 “-”来缩进表示层级：

/**
	 * 打印文件信息
	 * @param file 文件名称
	 * @param level 层次数(实际就是：第几次递归调用)
	 */
	public static void printFile(File file, int level) {
		// 输出层次
		for (int i = 0; i < level; i++) {
			System.out.print("-");
		}
		// 输出文件名
		System.out.println(file.getName());
		
		//如果file是目录，则获取子文件列表，并对每个子文件进行相同的操作
		if(file.isDirectory()) {
			File[] listFiles = file.listFiles();
			for (File f : listFiles) {
				//递归调用该方法：每调用一次层次+1
				printFile(f, level + 1);
			}
		}
	}

求斐波那契数列

斐波那契数列，有些地方说从0开始，有些地方说从1开始？？？
看百度百科怎么说：

斐波那契数列指的是这样一个数列：

自然中的斐波那契数列 自然中的斐波那契数列 这个数列从第3项开始，每一项都等于前两项之和。

我们按百度百科的方法用java代码实现：

/**
	 * 计算斐波那契数列
	 * @param n
	 * @return
	 */
	public static long fibRec(int n) {
		if(n == 1 || n == 2) {
			return 1;
		}
		return fibRec(n - 1) + fibRec(n - 2);
	}

打印文件和斐波那契数列完成代码及测试

package com.xzlf.recursion;

import java.io.File;

public class RecursionApp {
	
	public static void main(String[] args) {
		File file = new File("D:/Tomcat/apache-tomcat-7.0.69/webapps/manager");
		printFile(file, 0); // 使用递归打印文件信息
		System.out.println("=====================");
		long fibRec = fibRec(10); // 使用递归计算斐波那契数列
		System.out.println(fibRec);
	}
	
	/**
	 * 打印文件信息
	 * @param file 文件名称
	 * @param level 层次数(实际就是：第几次递归调用)
	 */
	public static void printFile(File file, int level) {
		// 输出层次
		for (int i = 0; i < level; i++) {
			System.out.print("-");
		}
		// 输出文件名
		System.out.println(file.getName());
		
		//如果file是目录，则获取子文件列表，并对每个子文件进行相同的操作
		if(file.isDirectory()) {
			File[] listFiles = file.listFiles();
			for (File f : listFiles) {
				//递归调用该方法：每调用一次层次+1
				printFile(f, level + 1);
			}
		}
	}
	
	/**
	 * 计算斐波那契数列
	 * @param n
	 * @return
	 */
	public static long fibRec(int n) {
		if(n == 1 || n == 2) {
			return 1;
		}
		return fibRec(n - 1) + fibRec(n - 2);
	}
}

代码运行结果：