Ankou: Guiding Greybox Fuzzing towards Combinatorial Difference
Abstract
P1: 介绍Greybox fuzzing;不足:现有的fitness函数无法区分达到相同coverage的不同program executions,导致容易困在局部最优值里(The problem is that current fitness functions only consider a union of data, but not their combination);
为了解决这个问题,不再被困在局部最优值,本文提出了Ankou
特点: greybox, 能够识别不同的执行信息组合(recognize different combinations of exec)
实验:
竞品软件: AFL, Angora
效果: 1.94x-8.0x more effective in finding bugs
1. Intro
P1: 介绍Fuzzing
P2: seed; fitness function(衡量test case的质量)
P3: 主流fitness function: 用code coverage
P4: 用code coverage的缺陷: 有些test case能探索宝贵的execution paths,但是因为没有覆盖新的基本块所以被忽略:例如,buffer overflow bugs在第一次覆盖的时候常常不会显现,需要重复执行一个循环若干次才会体现
P5: fitness function需要满足:
C1: informative: 能够量化程序执行之间的差异
C2: 算起来快
C3: 不应该接受过多seeds,以handle them in a practical manner
P6: C1: fitness function往往在1. 决定一个种子是否应该选取 2. 一个种子是否比其他种子更应该选取 之间不可得兼
P7: C2
P8: C3
P9: distance-based fuzzing:
C1: distance-based fitness functions
C2: dynamic PCA
C3: adaptive seed pool update
P10: distance-based fitness function: 通过测量两次execution中的执行到的branches的组合来给这两次执行的行为相似性打分
P11: 引入distance-based fitness function使得fuzzer的执行减慢13.22倍,为此,用dynamic PCA
P12,13:PCA, dynamic PCA: 让PCA增量计算
P13: we can compare test cases based on their fitness to actively decide the sensitivity of the pool update function
2. Background
2.1 Fitness and Local Optimum Problem
P1: we say we have reached a local optimum as we cannot obtain any more test cases that fulfill our fitness criterion even through we have not yet tested all possible executions of the PUT.
P2: 举例coverage的局限
P3: AFL branch-hit-count state
P4: 举例AFL coverage的局限
2.2 PCA
rt
3. Distance-based Fuzzing Fitness
P1: 本文认为AFL的branch-hit-count states已经提供了判断test case作为未来种子潜力的足够信息
P2: 相同覆盖但是不同AFL覆盖的两次执行应该有不同的向量表示
3.1 Fitness as Distance between Vectors
用欧几里得距离作为衡量两个branch-hit-count execution的距离。用当前test case到全体已经选择了的种子库的最小距离作为当前种子的noverty
3.2 Impracticality of Distance based Fitness
O(mn)的复杂度使得该距离衡量方法过于不可行。
改进措施
- M-tree
- PCA
4. Dynamic PCA

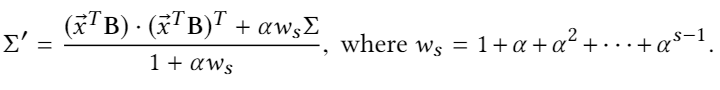
5. Distance-based fuzzing
5.1 Adaptive Seed Pool Update

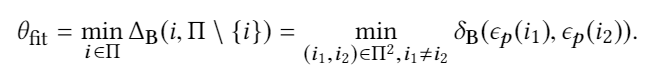
阈值就是全局距离最小值
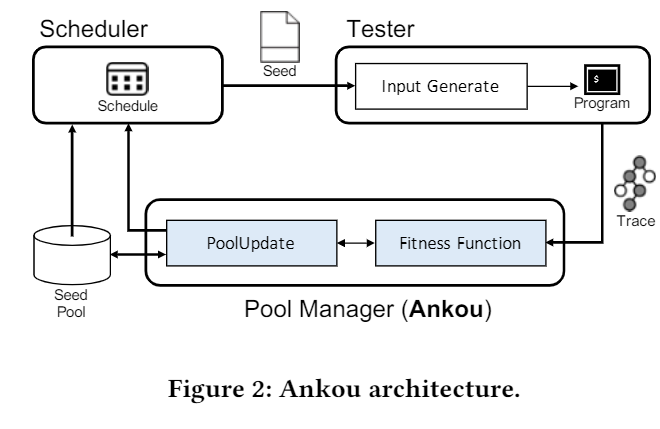
5.2 Ankou Architecture