UVA LA 3667 Ruler 搜索，迭代搜索 难度: 0

题目

https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1668

题意

给n种距离di，现在要设计一个m刻度的赤字，使得每个di都可以直接量出来。第一个刻度永远是0，数据保证刻度数目小于等于7.n <= 50。

思路

由于m最多为7，而m之前是不知道的，因此最好用迭代搜索，一开始就限制用多少刻度，而不是动态扩展。

如果由小到大枚举，那么就可能出现目前di应该要过几个回合再安排更优的情况，也就是说应该要放在现在已有的某个区间中间，将来才有的某个区间一端。而从大到小枚举，则没有将来的区间能够容纳di。

感想：

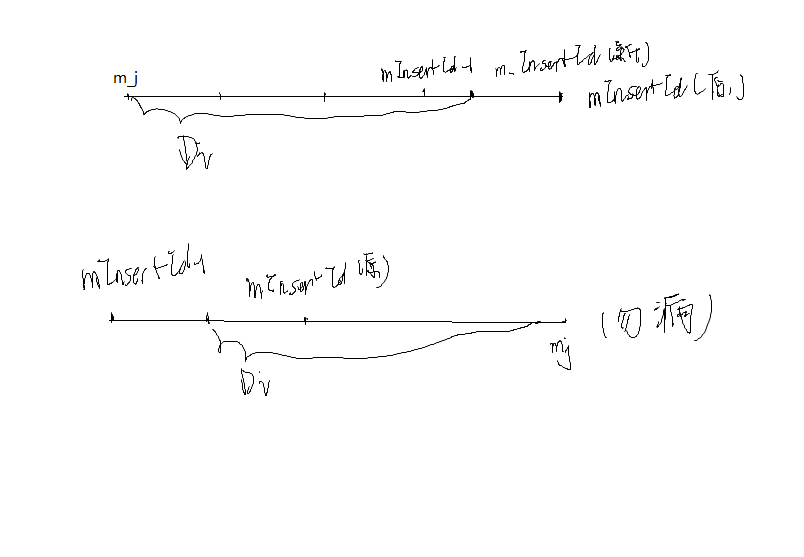
1. 一开始只考虑了把当前di放在mj作为起点的情况，没有想到把mj作为重点的情况。

大致如图：

代码

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <vector>
#include <map>
#include <set>
using namespace std;
typedef pair<int, int> Pair;
typedef long long ll;
const int MAXN = 55;
int a[MAXN];
int n;
vector<int> slots;
int prefixSum[10];

int removeDup(int* b, int n) {
	sort(b, b + n);
	int newn = 0;
	for (int i = 0; i < n; i++) {
		if (i && b[i] <= b[i - 1])continue;
		b[newn++] = b[i];
	}
	return newn;
}
int getMinM(int n) {
	int m = 1;
	int num = 1;
	while (num < n + 1) {
		m += 1;
		num <<= 1;
	}
	return m;
}

bool alreadySatisfied(int di) {
	for (int i = (int)slots.size() - 1; i > 0 && prefixSum[i] >= di; i--) {
		int leadingSlotD = prefixSum[i] - di;
		if (leadingSlotD == 0)return true;
		if (binary_search(prefixSum, prefixSum + i, leadingSlotD))return true;
	}
	return false;
}

void updatePrefixSum() {
	for (int i = 1; i < slots.size(); i++) {
		prefixSum[i] = prefixSum[i - 1] + slots[i];
	}
}

bool iddfs(int sId, int remainslots) {
	if (sId < 0)return true;
	if (alreadySatisfied(a[sId])) {
		return iddfs(sId - 1, remainslots);
	}
	if (remainslots == 0)return false;
	int nowSlotNum = slots.size();
	for (int i = nowSlotNum - 1; i > 0 && prefixSum[i] > a[sId]; i--) {//insertId - 1, a[sid], insertedId, i
		int insertId = i;
		for (; insertId > 0 && prefixSum[i] - prefixSum[insertId - 1] < a[sId]; insertId--) {}
		int newd = prefixSum[i] - prefixSum[insertId - 1] - a[sId];
		if (insertId < nowSlotNum)slots[insertId] -= newd;
		slots.insert(slots.begin() + insertId, newd);
		updatePrefixSum();
		if (iddfs(sId - 1, remainslots - 1))return true;
		slots.erase(slots.begin() + insertId);
		if (insertId < nowSlotNum)slots[insertId] += newd;
		updatePrefixSum();
	}
	for (int i = 0; i < nowSlotNum; i++) {//i, insertedId - 1, a[sid], insertedId
		int insertId = i + 1;
		for(;insertId < nowSlotNum && prefixSum[insertId] - prefixSum[i] < a[sId];insertId++){}
		int newd = a[sId] - prefixSum[insertId - 1] + prefixSum[i];
		if(insertId < nowSlotNum)slots[insertId] -= newd;
		slots.insert(slots.begin() + insertId, newd);
		updatePrefixSum();
		if (iddfs(sId - 1, remainslots - 1))return true;
		slots.erase(slots.begin() + insertId);
		if (insertId < nowSlotNum)slots[insertId] += newd;
		updatePrefixSum();
	}
	return false;
}

int main() {
	int T;
	freopen("C:\Users\Iris\source\repos\ACM\ACM\input.txt", "r", stdin);
	//freopen("C:\Users\Iris\source\repos\ACM\ACM\output.txt", "w", stdout);
	//scanf("%d", &T);
	//cin >> T;
	for (int ti = 1; scanf("%d", &n) == 1 && n; ti++) {
		for (int i = 0; i < n; i++) {
			scanf("%d", a + i);
		}
		n = removeDup(a, n);
		int minM = getMinM(n);
		int m = minM;
		for (; m <= 7; m++) {
			memset(prefixSum, 0, sizeof prefixSum);
			slots.clear();
			slots.push_back(0);
			if (iddfs(n - 1, m -1)) {
				break;
			}
		}
		printf("Case %d:
%d
", ti, m);
		for (int i = 0; i < m; i++) {
			printf("%d%c", prefixSum[i], (i == m - 1) ? '
': ' ');
		}
	}
	return 0;
}