题解【洛谷P2668】[NOIP2015]斗地主

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的 $ A $ 到 $ K $ 加上大小王的共 $ 54 $ 张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：$ 3 < 4 < 5 < 6 < 7 < 8 < 9 < 1 0 < J < Q < K < A < 2 < $ 小王 $ < $ 大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由 $ n $ 张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。具体规则如下：

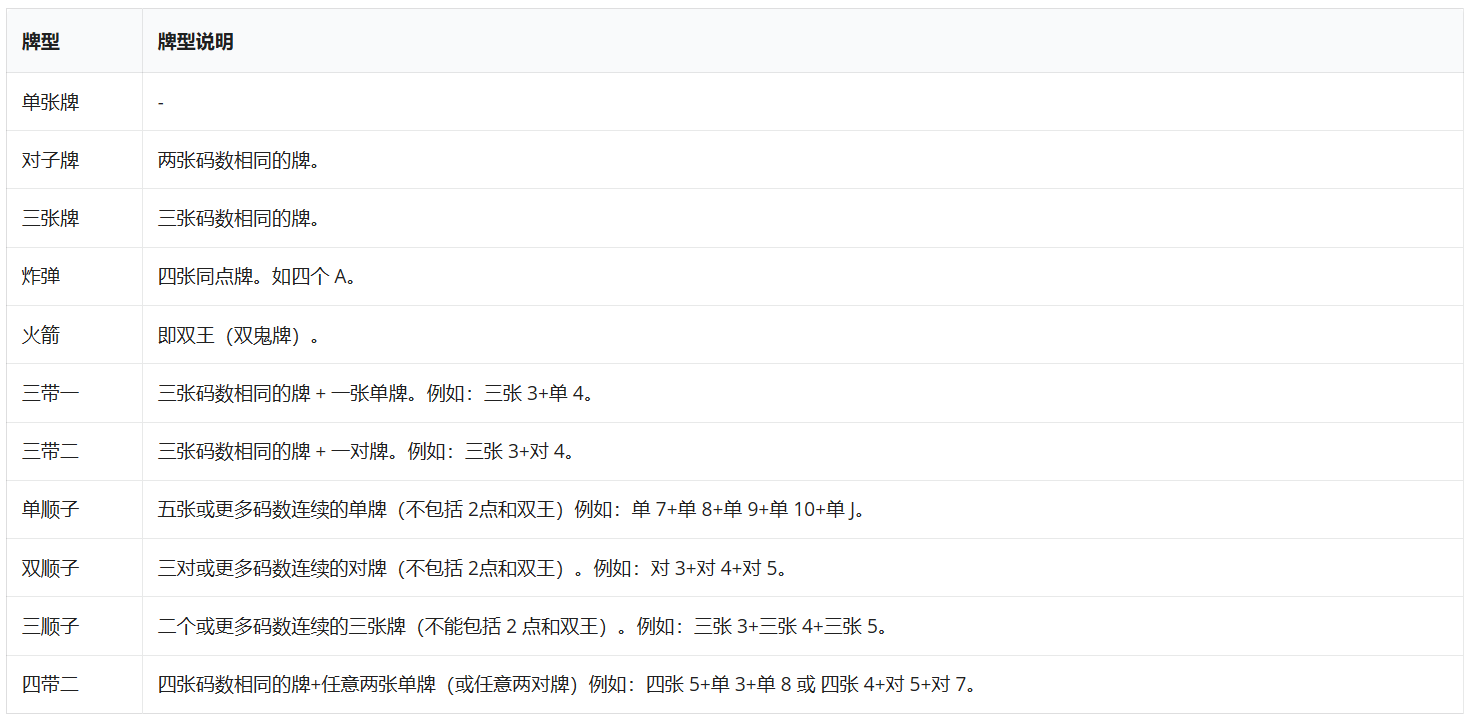
另外，在顺牌（单顺子、双顺子、三顺子）中，牌的花色不要求相同。

输入格式

第一行包含用空格隔开的 $ 2 $ 个正整数 $ T (，) N $，表示手牌的组数以及每组手牌的张数。

接下来 $ T $ 组数据，每组数据 $ N $ 行，每行一个非负整数对 $ A_i, B_i $，表示一张牌，其中 $ A_i $ 表示牌的数码，$ B_i $ 表示牌的花色，中间用空格隔开。特别的，我们用 $ 1 $ 来表示数码 $ A (，) 11 $ 表示数码 $ J (，) 12 $ 表示数码 $ Q (，) 13 $ 表示数码 $ K $；黑桃、红心、梅花、方片分别用 $ 1 - 4 $ 来表示；小王的表示方法为 0 1 ，大王的表示方法为 0 2。

输出格式

共 $ T $ 行，每行一个整数，表示打光第 $ i $ 组手牌的最少次数。

样例

样例输入 1

1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1

样例输出 1

3

样例输入 2

1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2

样例输出 2

6

数据范围与提示

题解

看到这么小的数据范围，应该一眼就能想到状压DP搜索。

的确，这是一道非常裸的搜索题。

直接暴力搜索即可。

哇我这么快就切了一道蓝题

这样想你就太天真了。

提交后发现，这样做只会得到(30)分。

为什么呢？让我们分析一下原因：

1. 我们每一次都枚举了所有可行的状态，冗余状态太多。

2. 会搜一些对题目答案没有任何影响的状态。

   ……

其实这样的根本原因就是：没有一个搜索的顺序。

按照正常的打牌者的角度去思考，你会发现：我们每一次都是先出顺子，在考虑带牌，最后才是单牌/炸弹/对子。

我们这样去搜索就可以(mathrm{AC})。

但是，你还会发现一个新问题：如果拆牌打所需次数更少呢？

可以看到最后一句话：数据保证：所有的手牌都是随机生成的。

而我们在打牌时很少会有拆牌方案更好的情况。

那么出现这个问题的几率就微乎其微了。

这个题的数据经过了特殊构造，可以卡掉没有考虑拆牌方案的做法。

代码

我太懒了，没有考虑拆牌的情况QwQ

/********************************
	Author: csxsl
	Date: 2019/10/28
	Language: C++
	Problem: P2668
********************************/
#include <bits/stdc++.h>
#define itn int
#define gI gi

using namespace std;

inline int gi()
{
	int f = 1, x = 0; char c = getchar();
	while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
	while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return f * x;
}

inline long long gl()
{
	long long f = 1, x = 0; char c = getchar();
	while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
	while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return f * x;
}

int t, n, a[25], ans;

void dfs(int now)//搜索主过程
{
	if (now >= ans) return;//最优性剪枝
	//先考虑单顺子
	int ps = 0;//顺子的对数
	for (int i = 3; i <= 14; i+=1)//枚举从3~A
	{
		if (a[i] < 1) ps = 0;//没有牌了，顺子断了
		else 
		{
			++ps;//牌数+1
			if (ps >= 5)//对数>=5，可以直接出了
			{
				for (int j = i; j >= i - ps + 1; j-=1) --a[j];//出牌
				dfs(now + 1);//递归下一步
				for (int j = i; j >= i - ps + 1; j-=1) ++a[j];//回溯时加上牌的张数
			}
		}
	}
	//双顺子
	ps = 0;//记得清零对数
	for (int i = 3; i <= 14; i+=1)//枚举3~A
	{
		if (a[i] < 2) ps = 0;//牌数<=1，顺子断了
		else 
		{	
			++ps;//对数+1
			if (ps >= 3)//对数>=3，可以出牌了
			{
				for (int j = i; j >= i - ps + 1; j-=1) a[j] -= 2;//出牌
				dfs(now + 1);//递归下一步
				for (int j = i; j >= i - ps + 1; j-=1) a[j] += 2;//进行回溯，加上那个原来的牌数
			}
		}
	}
	//三顺子
	ps = 0;//清零对数
	for (int i = 3; i <= 14; i+=1)//枚举3~A
	{
		if (a[i] < 3) ps = 0;//牌数不够3张，顺子断了
		else 
		{
			++ps;//对数+1
			if (ps >= 2)//对数>=2，可以出牌了
			{
				for (int j = i; j >= i - ps + 1; j-=1) a[j] -= 3;//打出三顺子
				dfs(now + 1);//递归下一步
				for (int j = i; j >= i - ps + 1; j-=1) a[j] += 3;//回溯时加上打出的牌数
			}
		}
	}
    
	//考虑带牌的情况
	for (int i = 2; i <= 14; i+=1)//枚举2~A，因为2也可以进行带牌
	{
		if (a[i] == 3)//正好有3张牌
		{
			//三带一
			a[i] -= 3;
			
			for (int j = 2; j <= 15; j+=1)//枚举2~大小王
			{
				if (j == i || a[j] <= 0) continue;//带的牌和那三张牌一样或者没有这张牌就直接枚举下一张牌
				--a[j];//出牌
				dfs(now + 1);//递归下一步
				++a[j];//回溯
			}
			
			//三带二
			for (int j = 2; j <= 14; j+=1)//枚举2~A
			{
				if (j == i || a[j] <= 1) continue;//跳过这张牌，与三带一的情况同理
				a[j] -= 2;//打出三代二
				dfs(now + 1);//递归进行下一步
				a[j] += 2;//回溯时加上带的对子
			}
			
			a[i] += 3;//回溯加上三张牌
		}
		else //可以选择三带一、三带二或四带二
		{
			a[i] -= 3;
			
			//三带一与上面情况相同
			for (int j = 2; j <= 15; j+=1)
			{
				if (j == i || a[j] <= 0) continue;
				--a[j];
				dfs(now + 1);
				++a[j];
			}
			
			//三带二同理
			for (int j = 2; j <= 14; j+=1)
			{
				if (j == i || a[j] <= 1) continue;
				a[j] -= 2;
				dfs(now + 1);
				a[j] += 2;
			}
			a[i] += 3;
			
			//四带二
			a[i] -= 4;
			
			//带两张单牌
			for (int j = 2; j <= 15; j+=1)//先从 2~大小王 枚举第一张单牌
			{
				if (j == i || a[j] <= 0) continue;//不能出
				--a[j];//先出一张
				for (int k = 2; k <= 15; k+=1)//枚举第二张单牌
				{
					if (a[k] <= 0 || j == k) continue;//不能和第一张单牌一样
					--a[k];//再出一张
					dfs(now + 1);//下一步
					++a[k];//回溯
				} 
				++a[j];//那会那一张牌
			}
			
			//带两对对子
			for (int j = 2; j <= 14; j+=1)//枚举第一对
			{
				if (j == i || a[j] <= 1) continue;
				a[j] -= 2;
				for (int k = 2; k <= 14; k+=1)//枚举第二对
				{
					if (j == k || a[k] <= 1) continue;
					a[k] -= 2;
					dfs(now + 1);
					a[k] += 2;
				}
				a[j] += 2;
			}
			
			a[i] += 4;//加上出的4张牌
		}
	}
	
	//单牌/炸弹/对子 最后考虑，因为它们都可以一次出完
	for (int i = 2; i <= 15; i+=1) if (a[i]) ++now;
	ans = min(ans, now);//更新答案
	return;//返回
}

int main()
{
	t = gi(), n = gI();
	while (t--)
	{
		ans = 0x7fffffff;
		memset(a, 0, sizeof(a));
        //多组数据，一定记得初始化！！！
		for (itn i = 1; i <= n; i+=1) 
		{
			int x = gi(), y = gi();
			if (x == 0) ++a[15];//大小王
			else if (x == 1) ++a[14];//A比K大，故位置为14
			else ++a[x];//统计每张牌出现的次数
		}
		dfs(0);//进行搜索
		printf("%d
", ans);//输出答案
	}
	return 0;
}

可以发现，我们每次输入的花色并没有任何用处。

因此，题目中输入的数据/给出的条件，并不一定都是有用的。