1、数据冗余导致的问题:冗余存储、更新异常、插入异常、删除异常。
2、函数依赖:一种完整性约束。
在关系模式r(R)中,α属于R,β属于R。
1)α函数确定β(β函数依赖于α):记作α→β,对于任意合法关系r及其中任两个元组ti和tj,i≠j,若ti[α]=tj[α],则ti[β]=tj[β]。
2)非平凡函数依赖和平凡函数依赖:若α→β,但β不属于α,则称α→β是非平凡函数依赖;否则,若β不属于α,则称α→β是平凡函数依赖。

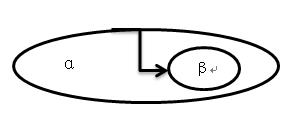
非平凡函数依赖 平凡函数依赖
3)完全函数依赖和部分函数依赖:α→β是非平凡函数依赖,若对任意的γ含于α,γ→β都不成立,则称α→β是完全函数依赖,简称完全依赖;否则,若存在非空的γ含于α,使γ→β成立,则称α→β是部分函数依赖,简称部分依赖。
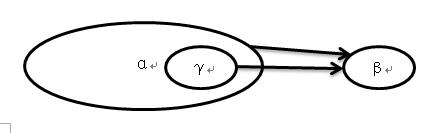
部分依赖α→β的依赖图
4)传递函数依赖
γ属于R,若α→β,β→γ,则必存在函数依赖α→γ,若α→β,β→γ和α→γ都是非平凡函数依赖,且β不依赖于α,则称α→γ是传递函数依赖,简称传递依赖。
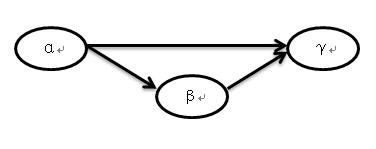
传递依赖α→γ的依赖图
3、函数依赖集闭包
1)逻辑蕴涵:若给定函数依赖集F,可以证明其他函数依赖也成立,则称这些函数依赖被F逻辑蕴涵。
2)闭包:令F为一函数依赖集,F逻辑蕴涵的所有函数依赖组成的集合称为F的闭包,记为F+。
3)属性集A的闭包:令r(R)为关系模式,F为属性依赖集,A属于R的属性集,则称在函数依赖集F下由A函数确定的所有属性的集合为F下属性集A的闭包,记为A+。
4)Armstrong公理及推论(可直接计算F+)
(1)自反律:若存在β属于α,则有α→β。
(2)增补律:若存在α→β,则有γα→γβ。
(3)传递律:若存在α→β且β→γ,则有α→γ。
(4)合并律:若存在α→β且α→γ,则有α→βγ。
(5)分解律:若存在α→βγ,则有α→β和α→γ。
(6)伪传递律:若存在α→β且βγ→δ,则有αγ→δ。
4、范式(关系模式要满足的条件)
1)目的:消除存储异常、减少数据冗余、保证数据完整性和存储效率。
2)基于函数依赖理论,范式的分类:
(1)第一范式(1NF)---码
如果一关系模式r(R)的每个属性对应的域值都是不可分的,则称r(R)属于第一范式。
目标:将基本数据划分成称为实体集或表的逻辑单元,当设计好每个实体后,需要为其指定主码。
| empno | ename | address | ||
| province | city | street | ||
非规范化的关系模式(地址的值域可分)
| empno | ename | province | city | street |
1NF规范化后的关系模式
(2)第二范式(2NF)---全部是码
如果一关系模式r(R),α属于r(R),若α包含在r(R)的摸个候选码中,则称α为主属性,否则α非主属性。
如果一关系模式r(R)属于第一范式,且所有非主属性都完全函数依赖于r(R)的候选码,则称r(R)属于第二范式。
目标:将只部分依赖于候选码(即依赖于候选码的部分属性)的非主属性通过关系模式分解移到其他表中去。
(3)第三范式(3NF)---仅仅是码
如果一关系模式r(R)属于第二范式,且所有非主属性都直接函数依赖于r(R)的候选码,且非主属性之间不存在依赖关系(即不存在非主属性传递依赖于候选码),则称r(R)属于第三范式。
目标:将只部分依赖于候选码(即依赖于候选码的部分属性)的非主属性通过关系模式分解移到其他表中去。
(4)Boyce-Codd范式(BCNF)
给定关系模式r(R)及函数依赖集F,若F+中的所有函数依赖α→β(α属于R,β属于R)至少满足下列条件之一:α→β是平凡函数依赖(即β属于α)、α是r(R)的一个超码(即α+包含R的全部属性),则称r(R)属于Boyce-Codd范式。