SVM

分割超平面

超平面:

数学中超平面是n维欧氏空间中余维度等于一的线性子空间。

超平面的最值与极值:

由于高维空间与一维空间不同，我们无法将一维空间的线性顺序（linear ordering）延伸到高维空间用于比较点的大小。所以，高维空间中的最值和极值的定义相对低维空间就变的复杂一些。对于集合而言，我们可以利用集合的定义说明集合最值的问题，集合S中的元素x为最小值，当且仅当S⊆x+K，这里x+K表示所有点的都大于等于x,例如，对于二维空间,如下图，点x1为集合S的最小值，因为对于浅色阴影部分而言,集合S1内的其他点则不满足该条件；对于点x2，其为集合S2的极小值，其中浅色阴影部分代表x－K部分，很明显，极小值并不是唯一的，因为点x2所在的直线上均为集合的极小值。

支撑超平面:

对于凸集S而言，x0为集合S边界上的一点$（x0∈bd S = cl S∖int S）$，如果aTx≤aTx0, a≠0，那么超平面{x∣aTx=aTx0}被称为集合S在点x0处的超平面。支持超平面也可以理解为分割点x0和S的超平面，支持超平面的几何意义表示集合S上点x0的切线。支持超平面的实例如下图所示:可以是一个或是多个.

分割超平面:

两个不相交的凸集，可能可以找到无限个分割超平面，那么哪一个是最优的呢？我们一般认为，距离凸集最边边最远的超平面就是这个最优的超平面。而我们做分类的时候，类别集合一般都是样本点，因此凸集最边就是距离超平面最近的样本点。而远处的样本点对这条分割超平面没有影响（最终运算的结果也证明只有支持向量对分割超平面有影响）。如图:

　　

支持向量:(仿射函数)

那些有决定分割超平面的点叫做支持向量,如上图黄颜色的点

 

 支持向量机(Support Vector Machine)

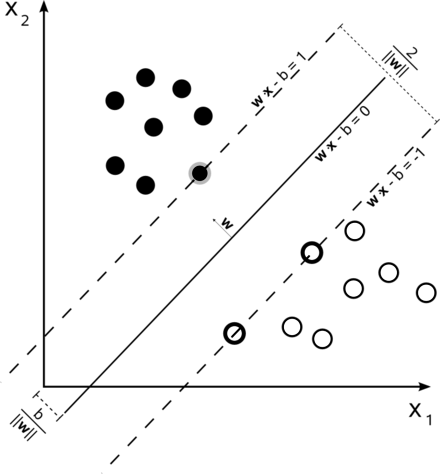
1.线性可分支持向量机(硬间隔支持向量机)

硬间隔:

如果这些训练数据是线性可分的，可以选择分离两类数据的两个平行超平面，使得它们之间的距离尽可能大。在这两个超平面范围内的区域称为“间隔”，最大间隔超平面是位于它们正中间的超平面。这些超平面可以由方程族：

或是

来表示。通过几何不难得到这两个超平面之间的距离是,因此要使两平面间的距离最大，我们需要最小化同时为了使得样本数据点都在超平面的间隔区以外，我们需要保证对于所有的

或是

这些约束表明每个数据点都必须位于间隔的正确一侧。

这两个式子可以写作：

可以用这个式子一起来得到优化问题：

此几何描述的一个显而易见却重要的结果是，最大间隔超平面完全是由最靠近它的那些确定的。这些叫做支持向量。

 

2.线性支持向量机(软间隔支持向量机)

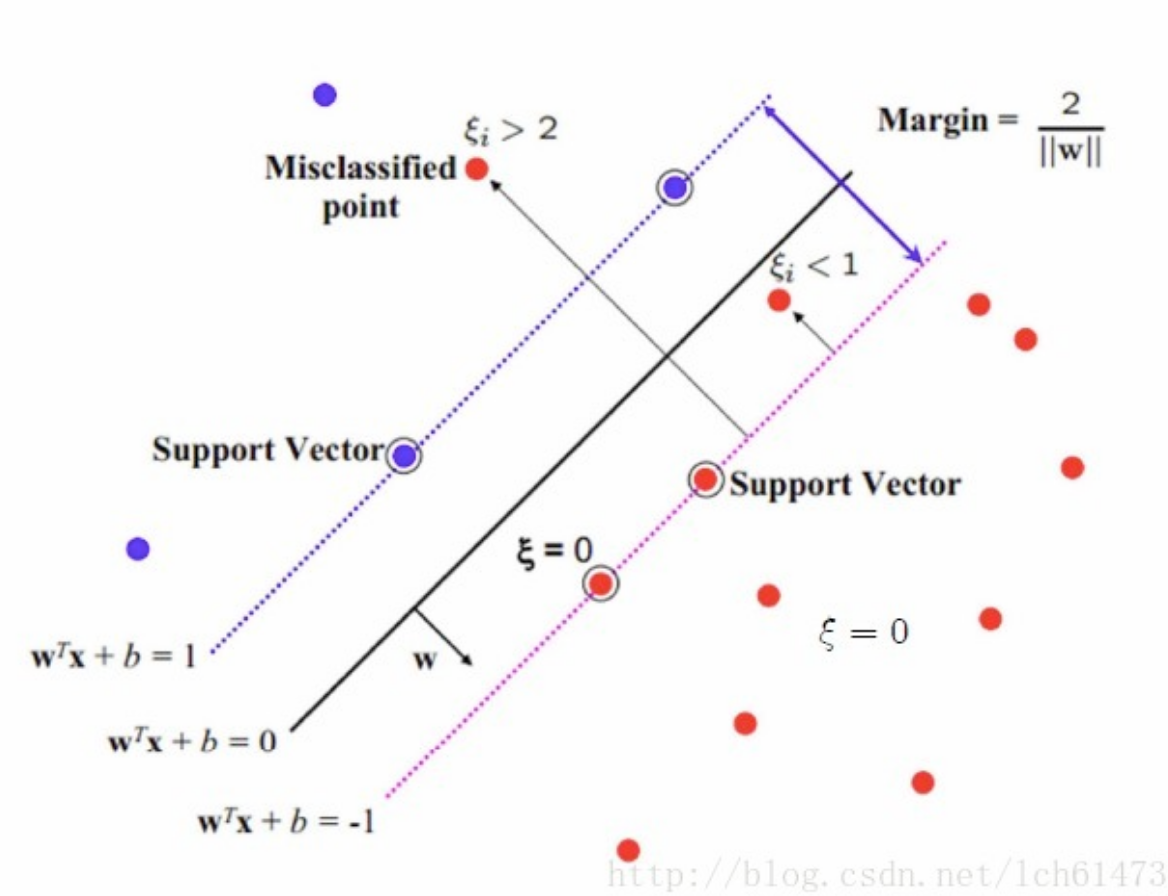
为了将SVM扩展到数据线性不可分的情况，我们引入铰链损失函数.

当约束条件 (1) 满足时（也就是如果 xi 位于边距的正确一侧）此函数为零。对于间隔的错误一侧的数据，该函数的值与距间隔的距离成正比。 然后我们希望最小化

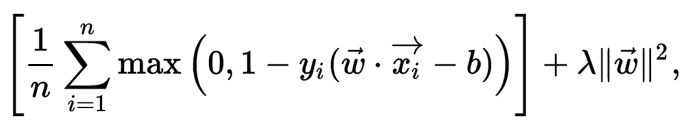
其中参数 λ  用来权衡增加间隔大小与确保xi位于间隔的正确一侧之间的关系。因此，对于足够小的 λ值，如果输入数据是可以线性分类的，则软间隔SVM与硬间隔SVM将表现相同，但即使不可线性分类，仍能学习出可行的分类规则。

 

3.非线性支持向量机

通过将核技巧应用于最大边界超平面来创建非线性分类器的方法。

常见的核函数包括：

 

如下图,非线性可分通过核函数映射到高维后变得线性可分:

 

支持向量机求解

简化为二次规划问题:

要求下列函数最小化

改写为目标函数可微的约束优化问题

求解上述问题的拉格朗日对偶，得到简化的问题

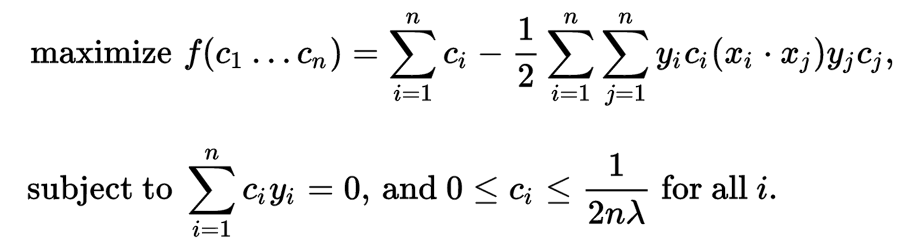
由于对偶最小化问题是受线性约束的 c i 的二次函数，所以它可以通过二次规划算法高效地解出。 这里变量 c i 定义为满足

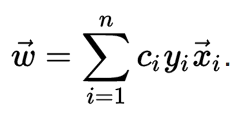
此外，当 xi  恰好在间隔的正确一侧时 c i = 0，且当 xi 位于间隔的边界时 0 < c i < ( 2 n λ ) − 1 。因此， w 可以写为支持向量的线性组合。 可以通过在间隔的边界上找到一个 xi并求解

得到偏移量b.

 

SMO求解法

 

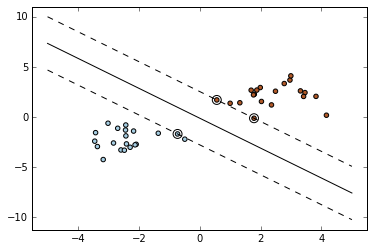
# -*- coding: utf-8 -*-

import numpy as np
import pylab as pl
from sklearn import svm

X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
Y = [0]*20 +[1]*20

clf = svm.SVC(kernel='linear')
clf.fit(X, Y)

w = clf.coef_[0]
a = -w[0]/w[1]
xx = np.linspace(-5, 5)
yy = a*xx - (clf.intercept_[0])/w[1]

b = clf.support_vectors_[0]
yy_down = a*xx + (b[1] - a*b[0])
b = clf.support_vectors_[-1]
yy_up = a*xx + (b[1] - a*b[0])

print("w: ", w)
print("a: ", a)


print("support_vectors_: ", clf.support_vectors_)
print("clf.coef_: ", clf.coef_)


pl.plot(xx, yy, 'k-')
pl.plot(xx, yy_down, 'k--')
pl.plot(xx, yy_up, 'k--')

pl.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
          s=80, facecolors='none')
pl.scatter(X[:, 0], X[:, 1], c=Y, cmap=pl.cm.Paired)

pl.axis('tight')
pl.show()