一、算法是什么?
算法(Algorithm):一个计算过程,解决问题的方法。
Niklaus Wirth说:“程序=数据结构+算法”
算法是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。

一个算法应该具有以下七个重要的特征:
- ①有穷性(Finiteness):算法的有穷性是指算法必须能在执行有限个步骤之后终止;
- ②确切性(Definiteness):算法的每一步骤必须有确切的定义;
- ③输入项(Input):一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输 入是指算法本身定出了初始条件;
- ④输出项(Output):一个算法有一个或多个输出,以反映对输入数据加工后的结果。没 有输出的算法是毫无意义的;
- ⑤可行性(Effectiveness):算法中执行的任何计算步骤都是可以被分解为基本的可执行 的操作步,即每个计算步都可以在有限时间内完成(也称之为有效性);
- ⑥高效性(High efficiency):执行速度快,占用资源少;
- ⑦健壮性(Robustness):对数据响应正确。
二、时间复杂度
时间复杂度:就是用来评估算法运行时间的一个式子(单位)。一般来说,时间复杂度高的算法比复杂度低的算法慢。
1、时间复杂度举例说明
类比生活的一些时间,估计时间:

来说说下面这些代码的时间复杂度是多少呢?
print('Hello World') # O(1)
for i in range(n): # O(n)
print('Hello World')
for i in range(n): # O(n^2)
for j in range(n):
print('Hello World')
for i in range(n): # O(n^3)
for j in range(n):
for k in range(n):
print('Hello World')
while n > 1: # O(log2n)或者O(logn)
print(n)
n = n // 2
当算法过程中出现循环折半的时候,复杂度式子中会出现logn。
2、常见的算法时间复杂度(按照效率排序)
大O简而言之可以认为它的含义是“order of”(大约是)。
Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<O(n2logn)< Ο(n^3)<…<Ο(2^n)<Ο(n!)
例如:
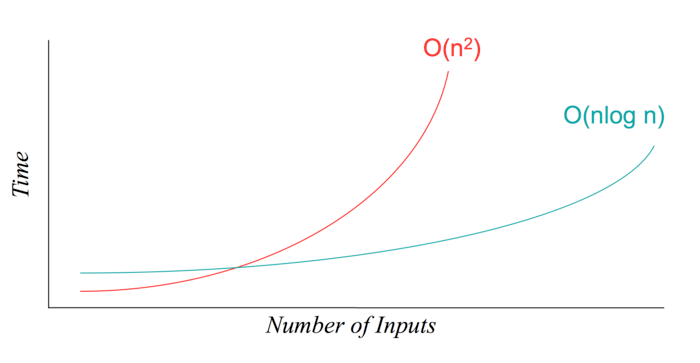
由图中我们可以看出,当 n 趋于无穷大时, O(nlogn) 的性能显然要比 O(n^2) 来的高
一般来说,只要算法中不存在循环语句,其时间复杂度就是 O(1)。
而时间复杂度又分为三种:
- 最优时间复杂度 (Best-Case)
- 平均时间复杂度 (Average-Case)
- 最差时间复杂度 (Worst-Case)
最差时间复杂度的分析给了一个在最坏情况下的时间复杂度情况,这往往比平均时间复杂度好计算,而最优时间复杂度一般没什么用,因为没人会拿一些特殊情况去评判这个算法的好坏。
3、时间复杂度总结
- 时间复杂度是用来估计算法运行时间的一个式子(单位)。
- 一般来说,时间复杂度高的算法比复杂度低的算法慢。
- 常见的时间复杂度(按效率排序):O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^2logn)<O(n^3)
- 复杂问题的时间复杂度(难解决的问题):O(n!) O(2n) O(nn)......
4、如果简单快速判断算法复杂度?
- 确定问题规模n
- 循环减半过程——>logn
- k层关于n的循环——>nk
复杂情况根据算法执行过程来判断。
三、空间复杂度
空间复杂度:用来评估算法内存占用大小的式子。
1、空间复杂度表示方式
算法使用了几个变量:O(1)
算法使用了长度为n的一维列表:O(n)
算法使用了m行n列的二维列表:O(mn)
2、空间换时间
算法宁可占用更多的内存也要让时间变快,分布式的运算也是一个空间换时间的过程。
四、回顾递归
1、递归的两个特点
- 调用自身
- 结束条件
由这两个特点判断函数是否是合法的递归:
# 没有结束条件不是合法的递归
def func1(x):
print(x)
func1(x-1)
# 结束条件结束不了,不是合法的递归
def func2(x):
if x>0:
print(x)
func2(x+1)
# 合法的递归: 先打印后递归
def func3(x):
if x>0:
print(x)
func3(x-1)
func3(5) # 5 4 3 2 1
# 合法的递归:先递归后打印,因此先打印最里层的 1
def func4(x):
if x>0:
func4(x-1)
print(x)
func4(5) # 1 2 3 4 5
2、递归实例:汉诺塔问题

大焚天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放到另一根柱子上。在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。64根柱子移动完毕之日就是世界毁灭之时。
(1)解决思路
n个盘子时:
- 把n-1个圆盘从A经过C移动到B;
- 把第n个圆盘从A移动到C;
- 把n-1个小圆盘从B经过A移动到C
(2)问题图解
将n-1个盘子看做一个整体,把最后一个盘子看做一个整体。
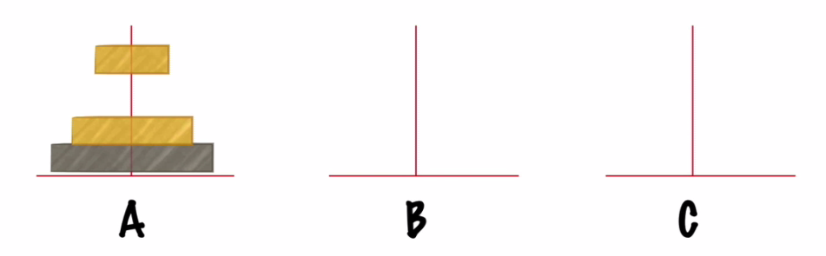
将n-1个盘子从A经C移动到B:
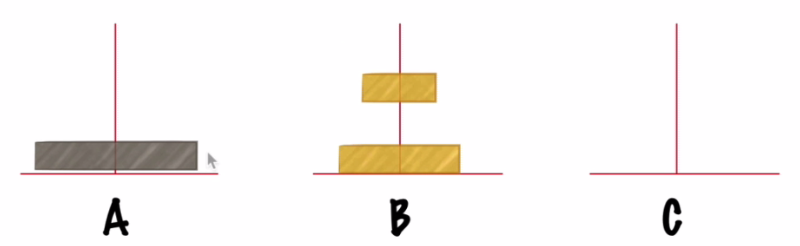
把第n个盘子从A移动到C:
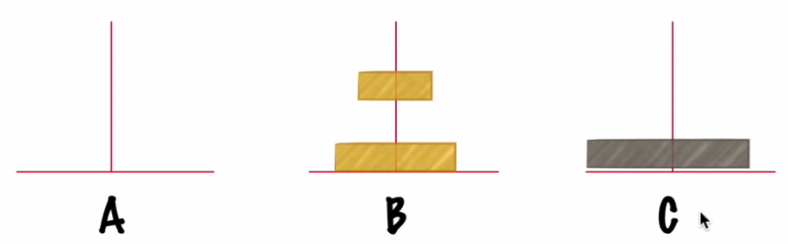
把n-1个小圆盘从B经过A移动到C:
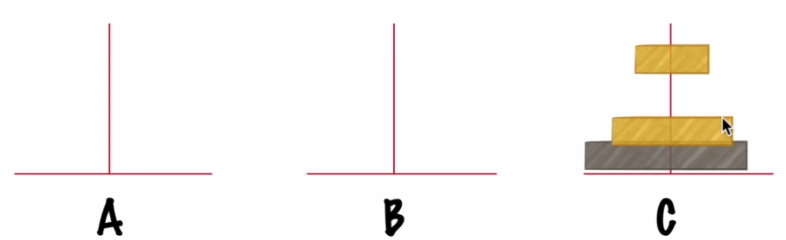
可以看到第一步、第三步就是比原问题规模小一的同样问题,因此就是原问题递归的一个子问题。
(3)代码实现
def hanoi(n, a, b, c):
"""
汉诺塔问题
:param n: 问题规模
:param a: 从哪个柱子
:param b: 经哪个柱子
:param c: 到哪个柱子
:return:
"""
if n > 0:
hanoi(n-1, a, c, b) # 将n-1个盘子从a经过c移动到b
print("moving from %s to %s" % (a, c)) # 将剩余的最后一个盘子从a移动到c
hanoi(n-1, b, a, c) # 将n-1个盘子从b经过a移动到c
n = int(input('请输入汉诺塔的层数:'))
hanoi(n, "A柱", "B柱", "C柱")
"""
请输入汉诺塔的层数:3
moving from A柱 to C柱
moving from A柱 to B柱
moving from C柱 to B柱
moving from A柱 to C柱
moving from B柱 to A柱
moving from B柱 to C柱
moving from A柱 to C柱
"""
(4)汉诺塔问题总结
汉诺塔移动次数的递推式:h(x)=2h(x-1)+1。
h(64)=18446744073709551615
假设婆罗门每秒搬一次盘子,总共需要5800亿年。