1.什么是LDA?
LDA线性判别分析也是一种经典的降维方法,LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“*投影后类内方差最小,类间方差最大*”。
什么意思呢? 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
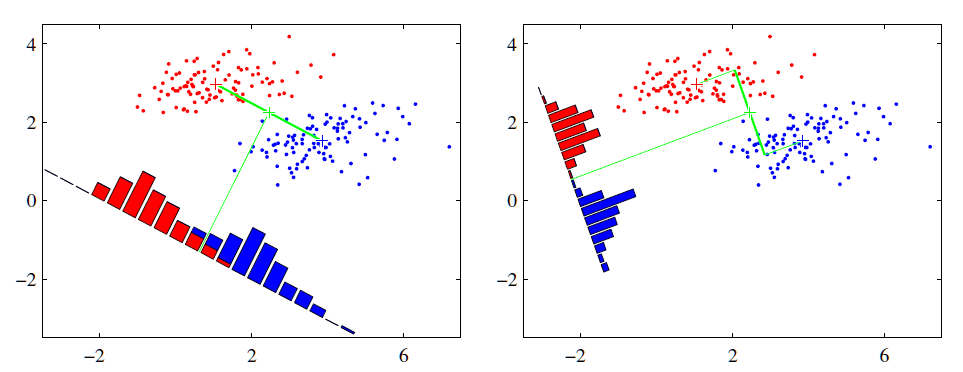
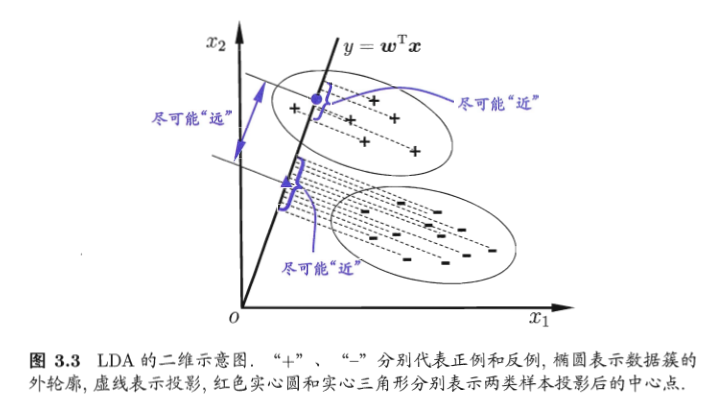
可能还是有点抽象,我们先看看最简单的情况。假设我们有两类数据分别为红色和蓝色,如下图所示,这些数据特征是二维的,我们希望将这些数据投影到一维的一条直线,让每一种类别数据的投影点尽可能的接近,而红色和蓝色数据中心之间的距离尽可能的大。
2.LDA原理
1 import numpy as np 2 from sklearn.discriminant_analysis import LinearDiscriminantAnalysis 3 from sklearn import datasets 4 5 import warnings 6 warnings.filterwarnings('ignore') 7 8 X,y=datasets.load_iris(True) 9 10 # 特征值和特征向量 11 # solver是求解方法,svd表示奇异值分解 12 lda = LinearDiscriminantAnalysis(solver='svd',n_components=2) 13 X_lda = lda.fit_transform(X,y) 14 X_lda[:5]

1 # 1、总的散度矩阵 2 # 协方差 3 St = np.cov(X.T,bias = 1) 4 5 # 2、类内的散度矩阵 6 # Scatter散点图,within(内) 7 Sw = np.full(shape = (4,4),fill_value=0,dtype=np.float64) 8 for i in range(3): 9 Sw += np.cov(X[y == i],rowvar = False,bias = 1) 10 Sw/=3 11 12 # 3、计算类间的散度矩阵 13 # Scatter between 14 Sb = St - Sw 15 16 # 4、特征值,和特征向量 17 eigen,ev = linalg.eigh(Sb,Sw) 18 display(eigen,ev) 19 ev = ev[:, np.argsort(eigen)[::-1]] 20 21 # 5、删选特征向量,进行矩阵运算 22 X.dot(ev)[:,:2]
计算得到的结果:
3.使用
使用和其他都一样,注意参数的含义
4.比较PCA和LDA
相同点:
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布【正态分布】。
不同点:
1)LDA是有监督的降维方法,而PCA是无监督的降维方法
2)LDA降维最多降到类别数**k-1**的维数,而PCA没有这个限制。
3)LDA除了可以用于降维,还可以用于分类。
4)LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。
5.机器学习中的监督学习和无监督学习
监督学习:
从给定的训练数据集中学习出一个函数(模型参数),当新的数据到来时,可以根据这个函数预测结果。监督学习的训练集要求包括输入输出,也可以说是特征和目标。训练集中的目标是由人标注的。
常见的有监督学习算法:回归分析和统计分类。最典型的算法是KNN和SVM。
无监督学习:
输入数据没有被标记,也没有确定的结果。样本数据类别未知,需要根据样本间的相似性对样本集进行分类(聚类,clustering)试图使类内差距最小化,类间差距最大化。通俗点将就是实际应用中,不少情况下无法预先知道样本的标签,也就是说没有训练样本对应的类别,因而只能从原先没有样本标签的样本集开始学习分类器设计。
无监督学习的方法分为两大类:
(1)一类为基于概率密度函数估计的直接方法:指设法找到各类别在特征空间的分布参数,再进行分类。
(2)另一类是称为基于样本间相似性度量的简洁聚类方法:其原理是设法定出不同类别的核心或初始内核,然后依据样本与核心之间的相似性度量将样本聚集成不同的类别。
利用聚类结果,可以提取数据集中隐藏信息,对未来数据进行分类和预测。应用于数据挖掘,模式识别,图像处理等。
PCA和很多deep learning算法都属于无监督学习。