Educational Codeforces Round 38 (Rated for Div. 2) ABCD

A. Word Correction

Victor tries to write his own text editor, with word correction included. However, the rules of word correction are really strange.

Victor thinks that if a word contains two consecutive vowels, then it's kinda weird and it needs to be replaced. So the word corrector works in such a way: as long as there are two consecutive vowels in the word, it deletes the first vowel in a word such that there is another vowel right before it. If there are no two consecutive vowels in the word, it is considered to be correct.

You are given a word s. Can you predict what will it become after correction?

In this problem letters a, e, i, o, u and y are considered to be vowels.

Input

The first line contains one integer n (1 ≤ n ≤ 100) — the number of letters in word s before the correction.

The second line contains a string s consisting of exactly n lowercase Latin letters — the word before the correction.

Output

Output the word s after the correction.

Examples

input

Copy

5
weird

output

Copy

werd

input

Copy

4
word

output

Copy

word

input

Copy

5
aaeaa

output

Copy

a

Note

Explanations of the examples:

1. There is only one replace: weird  werd;
2. No replace needed since there are no two consecutive vowels;
3. aaeaa  aeaa  aaa  aa  a.

 模拟题

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 110;
map<char,int> mp;
int main() {
    mp['a'] = mp['e'] = mp['i'] = mp['o'] = mp['u'] = mp['y']= 1;
    int n;
    cin >>n;
    string s, ss;
    cin >> s;
    for(int i = 0; i < n; i ++) {
        int j = i;
        while(mp[s[i]] && mp[s[i+1]] & i+1 < n) i++;
        ss += s[j];
    }
    cout << ss << endl;
    return 0;
}

B. Run For Your Prize

You and your friend are participating in a TV show "Run For Your Prize".

At the start of the show n prizes are located on a straight line. i-th prize is located at position ai. Positions of all prizes are distinct. You start at position 1, your friend — at position 106 (and there is no prize in any of these two positions). You have to work as a team and collect all prizes in minimum possible time, in any order.

You know that it takes exactly 1 second to move from position x to position x + 1 or x - 1, both for you and your friend. You also have trained enough to instantly pick up any prize, if its position is equal to your current position (and the same is true for your friend). Carrying prizes does not affect your speed (or your friend's speed) at all.

Now you may discuss your strategy with your friend and decide who will pick up each prize. Remember that every prize must be picked up, either by you or by your friend.

What is the minimum number of seconds it will take to pick up all the prizes?

Input

The first line contains one integer n (1 ≤ n ≤ 105) — the number of prizes.

The second line contains n integers a1, a2, ..., an (2 ≤ ai ≤ 106 - 1) — the positions of the prizes. No two prizes are located at the same position. Positions are given in ascending order.

Output

Print one integer — the minimum number of seconds it will take to collect all prizes.

Examples

input

Copy

3
2 3 9

output

Copy

8

input

Copy

2
2 999995

output

Copy

5

Note

In the first example you take all the prizes: take the first at 1, the second at 2 and the third at 8.

In the second example you take the first prize in 1 second and your friend takes the other in 5 seconds, you do this simultaneously, so the total time is 5.

 求最接近5e5的数。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+10;
int a[N];
int main() {
    int n;
    cin >> n;
    for(int i = 0; i < n; i ++) {
        cin >> a[i];
        if(a[i] > 5e5) a[i] = 1e6-a[i]+1;
    }
    sort(a,a+n);
    cout << a[n-1]-1 << endl;
    return 0;
}
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+10;
int a[N];
int main() {
    int n;
    cin >> n;
    for(int i = 0; i < n; i ++) {
        cin >> a[i];
        if(a[i] > 5e5) a[i] = 1e6-a[i]+1;
    }
    sort(a,a+n);
    cout << a[n-1]-1 << endl;
    return 0;
}

C. Constructing Tests

Let's denote a m-free matrix as a binary (that is, consisting of only 1's and 0's) matrix such that every square submatrix of size m × m of this matrix contains at least one zero.

Consider the following problem:

You are given two integers n and m. You have to construct an m-free square matrix of size n × n such that the number of 1's in this matrix is maximum possible. Print the maximum possible number of 1's in such matrix.

You don't have to solve this problem. Instead, you have to construct a few tests for it.

You will be given t numbers x1, x2, ..., xt. For every 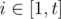, find two integers ni and mi (ni ≥ mi) such that the answer for the aforementioned problem is exactly xi if we set n = ni and m = mi.

Input

The first line contains one integer t (1 ≤ t ≤ 100) — the number of tests you have to construct.

Then t lines follow, i-th line containing one integer xi (0 ≤ xi ≤ 109).

Note that in hacks you have to set t = 1.

Output

For each test you have to construct, output two positive numbers ni and mi (1 ≤ mi ≤ ni ≤ 109) such that the maximum number of 1's in a mi-free ni × ni matrix is exactly xi. If there are multiple solutions, you may output any of them; and if this is impossible to construct a test, output a single integer  - 1.

Example

input

Copy

3
21
0
1

output

Copy

5 2
1 1
-1

 1 的数量是n²-(n/m)²，所以当有x个1时，n的最小值是sqrt(x)+1，因为矩阵不可以全为1，n的最大时就是m的最小时，当然m不能等于1，不然全是0了。

所以m最小为2，当n²-(n/2)²大于x时就调出，然后在n的范围内计算m

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+10;
int main() {
    int t, x;
    cin >> t;
    while(t--) {
        cin >> x;
        if(x == 0) cout << "1 1
";
        else if(x == 1) cout << "-1
";
        else {
            int n = sqrt(x)+1, flag = 0;
            while(true){
                if(n*n-(n/2)*(n/2) > x) break;
                for(int i = 2; i <= n; i ++) {
                    int m = n/i;
                    if(x == n*n-m*m ) {
                        cout << n << ' ' << i << endl;
                        flag = 1;
                        break;
                    } else if(n*n-m*m > x) break;
                }
                if(flag)break;
                n++;
            }
            if(!flag) cout << "-1
";
        }
    }
    return 0;
}

D. Buy a Ticket

点击