对于 8 位的有符号数而言,它的范围在 -128~127。该数的范围若在 -127~127,那还好理解,但关键该数还可取值 -128。那 -128 是怎么来的呢?
-128 的来源
说法一
有人就说了,8 位的有符号数除了表示 -127~127,还剩下一个二进制数 “1000 0000B”没有用,这太浪费了,所以用来表示 -128。这种说法很明显是站不住脚的。原因主要有两个:1)既然浪费,那该二进制数也可用来表示除了 -128 之外的数;2)数学是一门严谨的语言,不存在如此模糊的说法。
说法二
还有一个说法,来自百度文库的一篇文章,即作者通过如下的列举法:
正数:补码跟原码一样 +127, 0111 1111 +126, 0111 1110 +125, 0111 1101 +124, 0111 1100 +123, 0111 1011 +122, 0111 1010 ... +4, 0000 0100 +3, 0000 0011 +2, 0000 0010 +1, 0000 0001 0, 0000 0000 (无正负之分) 负数: 值 原码 反码 补码 -1, 1000 0001, 1111 1110, 1111 1111 -2, 1000 0010, 1111 1101, 1111 1110 -3, 1000 0011, 1111 1100, 1111 1101 -4, 1000 0100, 1111 1011, 1111 1100 -5, 1000 0101, 1111 1010, 1111 1011 -6, 1000 0110, 1111 1001, 1111 1010 -7, 1000 0111, 1111 1000, 1111 1001 -8, 1000 1000, 1111 0111, 1111 1000 -9, 1000 1001, 1111 0110, 1111 0111 -10, 1000 1010, 1111 0101, 1111 0110 -11, 1000 1011, 1111 0100, 1111 0101 -12, 1000 1100, 1111 0011, 1111 0100 -13, 1000 1101, 1111 0010, 1111 0011 -14, 1000 1110, 1111 0001, 1111 0010 -15, 1000 1111, 1111 0000, 1111 0001 -16, 1001 0000, 1110 1111, 1111 0000 -17, 1001 0001, 1110 1110, 1110 1111 ... -24, 1001 1000, 1110 0111, 1110 1000 ... -99, 1110 0011, 1001 1100, 1110 0100 ... -124, 1111 1100, 1000 0011, 1000 0100 -125, 1111 1101, 1000 0010, 1000 0011 -126, 1111 1110, 1000 0001, 1000 0010 -127, 1111 1111, 1000 0000, 1000 0001
按照规律, -127 的补码再往下应该还有补码 “1000 0000”,该二进制数表示 -128。
作者的列举法看起来确实形象了许多,但却仍未能够解释根本的数学原理。
说法三
这种说法是个人的想法,不过跟说法二一样,都是为了解释而解释。
我们知道 -128 = -127 - 1,那我们就可以通过 -127 和 -1 的相加得到 -128 的补码了。而 -127 的补码为 1000 0001,-1 的补码为 1111 1111,两者相加得到的结果是 1 1000 0000。因为只有 8 位可表示,所以我们可以舍掉补码最高位 1,剩下的就表示 -128 的补码了,也即 -128 的补码为 1000 0000。
这种说法就更加问题多多,而且还牵扯到了溢出问题。
说法四
最靠谱的说法一定是来自严格的数学推导或定理。
一般而言,在计算机中对有符号数的表示方式采用的是 Two's complement (实际上就是补码)方法。它的数学公式如下:

这样我们很容易就可以得到下边几个例子:

同理可以得到:
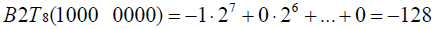
这样补码 “1000 0000” 表示 -128 的问题就可以解决了。我们因此知道,对于有 w 位补码(不是原码或反码),它能够表示的范围在:![]() 。
。
当然,用补码来计算我们得保证其运算过程的正确性。这方面可参考《深入理解计算机系统》第 2 章“信息的表示和处理”的第 2.3 节“整数运算”。
-128 + 127 = -1 ?
在实际研究中,还遇到一些感觉很奇怪的问题,例如 -128 加上 127 应该等于多少。我们从上文已经知道 -128 的补码是 1000 0000,而 127 的补码是 0111 1111,那 -128+127 的结果用补码表示就是 1111 1111。在思维没有切换到原码之前,总是将 1111 1111 当做 -127,而没有将其由补码转化为原码,从而导致理解上的错误。
所以,得时刻记住下图: